Solutions-Class-12-Physics-Chapter-12-Electromagnetic Induction-MSBSHSE

(B) 100 Wb

(A) BLv

(B) 30 mH

(A) 0.1 V

(A) 10 mJ

The phenomenon of production of emf in a conductor or circuit by a changing magnetic flux through the circuit is called electromagnetic induction.

Faraday's laws of electromagnetic induction :

• First law : Whenever there is a change in the magnetic flux associated with a circuit, an emf is induced in the circuit.
• Second law : The magnitude of the induced emf is directly proportional to the time rate of change of magnetic flux through the circuit.

Lenz’s law : The direction of the induced current is such as to oppose the change that produces it. The change that induces a current may be

• the motion of a conductor in a magnetic field or
• the change of the magnetic flux through a stationary circuit.

Explanation :

Consider Faraday's magnet− and− coil experiment.

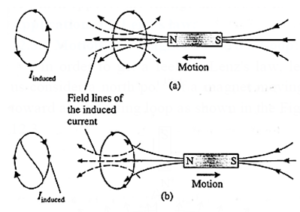
• If the bar magnet is moved towards the coil with its N− pole facing the coil, as in below Fig. (a), the number of magnetic lines of induction (pointing to the left) through the coil increases.
• The induced current in the coil sets up a magnetic field of its own pointing to the right (as given by Amperes right− hand rule) to oppose the growing flux due to the magnet.
• Hence, to move the magnet towards the coil against this repulsive flux of the induced current, we must do work. The work done shows up as electric energy in the coil.
• When the magnet is withdrawn, with its N− pole still facing the coil, the number of magnetic lines of induction (pointing left) through the coil decreases.
• The induced current reverses its direction to supplement the decreasing flux with its own, as shown in Fig. (b).
• Facing the coil along the magnet, the induced current is in the clockwise sense.
• The electric energy in the coil comes from the work done to withdraw the magnet, now against an attractive force.
• Thus, we see that Lenz’s law is a consequence of the law of conservation of energy.

Whenever a conductor or a part of it is moved in a magnetic field "cutting" magnetic field lines, or placed in a changing magnetic field, the free electrons in the bulk of the metal start circulating in closed paths equivalent to current− carrying loops.

These loop currents resemble eddies in a fluid stream and are hence called eddy or Foucault currents

Applications :

• Dead− beat galvanometer : A dead− beat galvanometer measures current by wounding a coil on a light aluminum frame, producing eddy currents that oppose rotation and bring the coil to rest quickly. This makes the galvanometer dead− beat.
• Electric brakes : In electric brakes, the interaction between eddy currents in a moving conductor and the field retards motion, making it useful for braking in vehicles. The coil's rotation in a magnetic field is a key component of this mechanism.

• As the copper disc enters and leaves the magnetic field, the changing magnetic flux through it induces eddy current in the disc.
• In both cases, Fleming's right hand rule shows that opposing magnetic force damps the motion.
• After a few swings, the mechanical energy becomes zero and the motion comes to a stop and the disc's heating due to the eddy current warms it, transforming the mechanical energy of the pendulum into thermal energy.

We assume that the inductors are so far apart that their mutual inductance is negligible.

If several inductances L_1, L_2, L_3,  ... are connected in parallel, then the total inductance is determined by using following relations:

1/L_Total = 1/L₁ + 1/L₂ + 1/L₃ + ...... (Parallel Combination)

Assuming that their mutual inductance can be ignored, the equivalent inductance of a parallel combination of two coils is given by

1/L_Total = 1/L₁ + 1/L₂

∴ L_Total = \(\frac{L_1L_2}{L_1+L_2}\)

Hence, the inductance of two coils connected in parallel is less than the inductance of either coil.

Suppose a thin conducting disc of radius R is rotated anticlockwise, about its axis, in a plane perpendicular to a uniform magnetic field of induction  (see Fig.)  points downwards.  Let the constant angular speed of the disc be ω.

Consider an infinitesimal element of radial thickness dr at a distance r from the rotation axis. In one rotation, the area traced by the element is dA =2 πrdr. Therefore, the time rate at which the element traces out the area is

\(\frac{dA}{dt}\) = frequency of rotation x dA = fdA

Where f = \(\frac{ω}{2π}\) is the frequency of rotation.

∴ \(\frac{dA}{dt}\) = \(\frac{ω}{2π}\)(2πrdr) = ωrdr

The total emf induced between the axle and the rim of the rotating disc is

| e | = ∫B\(\frac{dA}{dt}\)

= \(\int_0^R\)ωrdr

= Bω\(\int_0^R\)rdr

= Bω\(\frac{R^2}{2}\)

Given : l = 20 m, v = 10 m/s, B = 5 x 10^{− 5} T

The magnitude of the induced emf,

| e | = B l v = (5 × 10^{− 5})(20)(10) = 10^{− 2} V = 10 mV

Given : R = 0.3 m, f = 20 rps, B = 0.2 T

(a) The area swept out per unit time by a given radius = (the frequency of rotations) x (the area swept out per rotation) = f(πr²)

= (20)(3.142 × 0.3²) = 5.656 m²

(b) The time rate at which a given radius cuts magnetic flux = \(\frac{dΦ_m}{dt}\) = Bf(πr²)

= (0.2)(5.656) = 1.131 Wb/s

(c) The magnitude of the induced emf, | e | = \(\frac{dΦ_m}{dt}\) = 1.131 V

Given : M = 1.5 H, I_1i = 0, I_1f =10 A, Δt = 0.2 s

The flux linked per unit turn with the second coil due to current I_i in the first coil is

Φ₂₁ = MI₁

Therefore, the change in the flux due to change in I₁ is

ΔΦ₂₁ = M(ΔI₁) = M(I_1f − I_1i) = 1.5(10 − 0) = 15 Wb

Given : n = 1.5 x 10³ m^{− 1}, A = 25 x 10^{− 4} m², N_C = 150, I = 3A, Δt = 0.5 s,

μ₀ = 4π x 10^{− 7} H/m

(a) Magnetic flux density inside the solenoid, B = μ₀nI = (4π x 10^{− 7})(1500)(3)

= 5.656 × 10^{− 3} T = 5.656 mT

(b) Flux per unit turn through the coils of the solenoid, Φ_m = BA

Since the coil C is wound tightly over the solenoid, the flux linkage of C is

N_CΦ_m = N_CBA = (150)(5.656 × 10^{− 3})(25 × 10^{− 4})

= 2.121 x 10^{− 3} Wb = 2.121 mWb

(c) Initial flux through coil C, Φ_i = N_CΦ_m = 2.121 x 10^{− 3} Wb

Reversing the current in the solenoid reverses the flux through coil C, the magnitude remaining the same. But since the flux enters through the other face of the coil, the final flux through C is Φ_f = − 2.121 x 10^{− 3} Wb

Therefore, the average emf induced in coil C,

e =  \(− \frac{Φ_f− Φ_i}{Δt}\) = \(− \frac{(− 2.121− 2.121)×10^{− 3}}{0.5}\)

= 2 × 4.242 × 10^{− 3} = 8.484 x 10^{− 3} V = 8.484 mV

Given : N = 2000, A_i = 1.5 x 10^{− 4} m², A_f = 0, B = 0.6 T, Δ_t = 0.2s

Initial flux, NΦ_i = NBA_i = 2000(0.6)(1.5 × 10^{− 4}) = 0.18 Wb

Final flux, NΦ_f = 0, since the coil is withdrawn out of the field.

Induced emf, e = − N\(\frac{dΦ_m}{dt}\) = − N\(\frac{Φ_f− Φ_i}{Δt}\) = \(− \frac{0− 0.18}{0.2}\)  = 0.9 V

Given : l = 50 m, B = 6 x 10^{− 5} T, v = 400 m/s

The magnitude of the induced emf,

| e | = B l v = (6 × 10^{− 5})(400)(50) = 1.2 V

In one rotation, the wire traces out a circle of radius R, i.e., an area A = πR².

Therefore, the rate at which the wire traces out the area is

\(\frac{dA}{dt}\) = frequency or rotation x A = fA

If the angle between the uniform magnetic field  and the rotation axis is θ, the magnitude of the induced emf is

| e | = B\(\frac{dA}{dt}\)cos θ = BfA cos θ = Bf(πR²) cos θ

so that the required amplitude is equal to Bf(πR²).

Given: l = 1.75 m, v = 50 km/h = 50 x \(\frac{5}{18}\)  m/s, B_v = 5 x 10^{− 5} T

The area swept out by the wing per unit time = lv.

∴ The magnetic flux cut by the wing per unit time = \(\frac{dΦ_m}{dt}\) = B(l v)

= (5 × 10^{− 5})(1.75)( 50 x \(\frac{5}{18}\)) = 121.5 × 10^{− 5}

= 1.215 mWb/s

Therefore, the magnitude of the induced emf,

| e | = 1.215 mV

Given : M = 10 mH = 10^{− 2} H, I_1i = 5 A, I_1f = 1 A, Δt = 0.2 s, R = 592

The mutually induced emf in coil 2 due to the changing current in coil 1,

e₂₁ = − M\(\frac{ΔI_1}{Δt}\) = − M\(\frac{I_{1f}− I_{1i}}{Δt}\)\(\frac{1− 5}{0.2}\)  = − (10^{− 2})  = 0.2

If ΔQ₂ is the charge that flows through coil 2 due to the changing current in coil 1, the induced current in coil 2 is

I₂ = \(\frac{ΔQ_2}{Δt}\) = \(\frac{e_2}{R_2}\)

∴ ΔQ₂  = \(\frac{e_2}{R_2}\)Δt = \(\frac{0.2}{5}\)(0.2) = \(\frac{0.04}{5}\) = 0.008 C = 8 mC

Given : |e₂| = 9.6 x 10^{− 2} V,  \(\frac{dI_1}{dt}\) = 1.2 A/s

|e₂| = M\(\frac{dI_1}{dt}\)

Mutual Inductance, M = \(\frac{e_2}{dI_1/dt}\) = \(\frac{9.6×10^{-2}}{1.2}\) = 8 x 10^{− 2} = 80 mH

We assume the solenoid to be ideal and that all the flux from the solenoid passes through the outer coil. For a steady current I_S through the solenoid, the uniform magnetic field inside the solenoid is

B = μ₀nI_S = \(\frac{μ_0N_1I_S}{l}\)  …..(1)

n = N₁/l is the number of turns of the wire per unit length

Then, the magnetic flux through each turn of the coil due to the current in the solenoid is

Φ_CS = BA = \(\frac{μ_0N_1I_S}{l}\)A  …….(2)

Thus, mutual inductance of two coil is

M = \(\frac{N_2Φ_{CS}}{I_S}\) = \(\frac{μ_0N_1N_2I_S}{I_S×l}\) = \(\frac{μ_0N_1N_2}{l}\)

Given : L_P = L_S = 2 x 10^{− 4} H, M = 4 x 10^{− 6} H

M = K\(\sqrt{L_PL_S}\)

The coupling coefficient is

K = \(\frac{M}{\sqrt{L_PL_S}}\)

= \(\frac{4×10^{-6}}{\sqrt{(2×10^{-4})^2}}\)

= \(\frac{4×10^{-6}}{2×10^{-4}}\) = 2 x 10^{− 2}

Therefore, the percentage of flux of the primary reaching the secondary is = 0.02 × 100% = 2%

Given : l = 1 m, d = 1 cm, n = 100 cm^{− 1} = 10⁴ m^{− 1}, I = 100 A, μ₀ = 4π x 10^{− 7} H/m

The radius of cross section, r = d/2 = 0.5 cm = 5 × 10^{− 3} m

(a) Magnetic field inside the toroid,

B = μ₀nI = (4π x 10^{− 7})(10⁴)(100) = 0.4 × 3.142 = 1.257 T

(b) Self inductance of the toroid,

L = μ₀2πRn²A = μ₀n²lΑ = μ₀n²l(πr²)

=(4π x 10^{− 7})(10⁴)²(1) [π (5 × 10^{− 3})²]

= π² x 10^{− 3} = 9.87 × 10^{− 3} H = 9.87 mH

The area of the region, A = πs², remains constant while B = B(t) is a function of time.

Therefore, the induced emf,

e = \(-\frac{dΦ_m}{dt}\) = \(−\frac{d}{dt}\)(BA) = −A\(\frac{dB(t)}{dt}\) = − πs²\(\frac{dB(t)}{dt}\)