Notes
Topics to be learn :
|
We know area of any triangle = \(\frac{1}{2}\)x base x height.
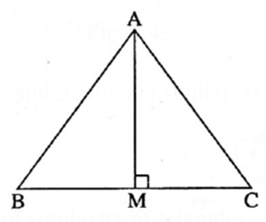
In the given figure, seg BC is the base and seg AM is the height of the triangle.
∴ A(ΔABC) = \(\frac{1}{2}\)x BC x AM
Ratio of areas of two triangles :
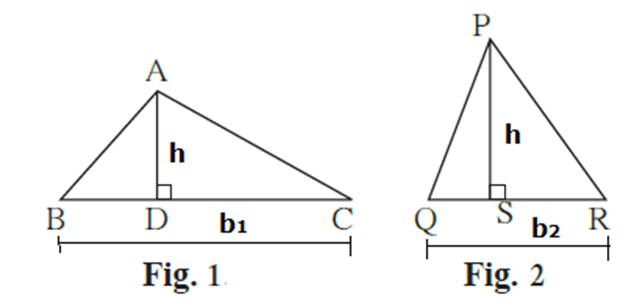
Statement : Ratio of areas of two triangles is equal to the ratio of the products of their bases and corresponding heights.
In ΔABC, seg AD is the height and BC is the base.
In ΔPQR, seg PS is the height and QR is the base
Proof : Area of any triangle = \(\frac{1}{2}\)x base x height.
∴A(ΔABC) = \(\frac{1}{2}\)x BC x AD and
A(ΔPQR) = \(\frac{1}{2}\)x QR x PS
\(\frac{A(ΔABC)}{A(ΔPQR)}=\frac{\frac{1}{2}×BC×AD}{\frac{1}{2}×QR×PS}\) = \(\frac{BC×AD}{QR×PS}\)
Hence the ratio of the areas of two triangles is equal to the ratio of the products of their bases and corresponding heights.
If the base, height and area of one triangle is denoted by b1, h1 and A1 respectively and that of the other triangle is denoted by b2, h2 and A2 respectively then
\(\frac{A_1}{A_2}=\frac{b_1×h_1}{b_2×h_2}\)
Suppose some conditions are imposed on these two triangles,
Condition 1: If the heights of both triangles are equal then-
Here, AD = PS = h
\(\frac{A(ΔABC)}{A(ΔPQR)}\)= \(\frac{BC×AD}{QR×PS}\)= \(\frac{BC×h}{QR×h}\)
∴\(\frac{A(ΔABC)}{A(ΔPQR)}\)= \(\frac{BC}{QR}\)
Thus for two triangles if h1 = h2 then \(\frac{A_1}{A_2}=\frac{b_1}{b_2}\)
Property : Areas of triangles with equal heights are proportional to their corresponding bases.
Condition 2 : If the bases of both triangles are equal then -
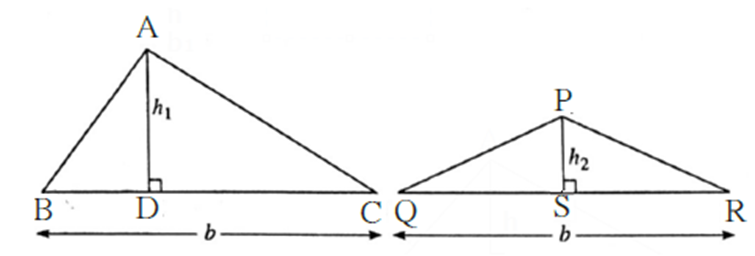
Here, BC = QR = b
\(\frac{A(ΔABC)}{A(ΔPQR)}\)= \(\frac{BC×AD}{QR×PS}\)= \(\frac{b×AD}{b×PS}\)
∴ \(\frac{A(ΔABC)}{A(ΔPQR)}\)= \(\frac{AD}{PS}\)
Thus for two triangles, if b1 = b2, then \(\frac{A_1}{A_2}=\frac{h_1}{h_2}\)
Property : Areas of triangles with equal bases are proportional to their corresponding heights.
Activity :
Fill in the blanks properly
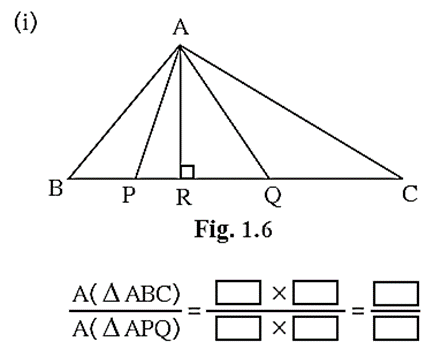
\(\frac{A(ΔABC)}{A(ΔAPQ)}\)= \(\frac{[BC]×[AR]}{[PQ]×[AR]}\)= \(\frac{[BC]}{[PQ]}\)
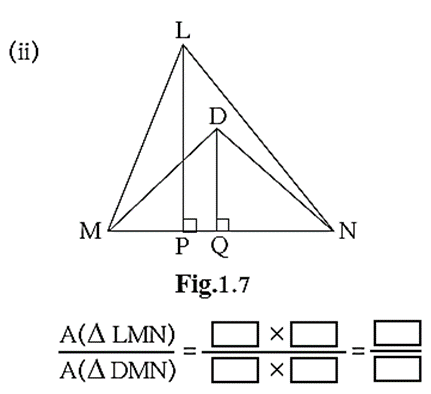
\(\frac{A(ΔLMN)}{A(ΔDMN)}\)= \(\frac{[MN]×[LP]}{[MN]×[DQ]}\)= \(\frac{[LP]}{[DQ]}\)
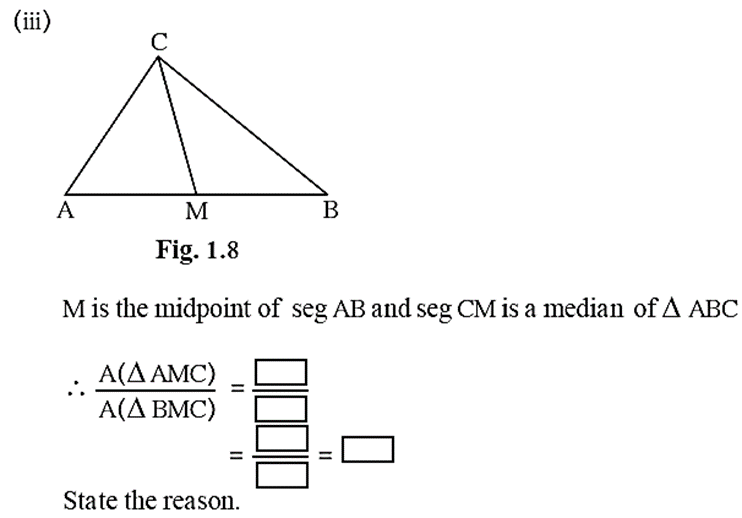
\(\frac{A(ΔAMC)}{A(ΔBMC)}\)= \(\frac{[AM]}{[BM]}\)
= \(\frac{[AM]}{[AM]}= 1\)
Reason : ΔAMC and ΔBMC are of equal bases ['.' AM = MB] also they have a common vertex C and their bases AM and MB lie on the same line AB, they are of equal heights.
ΔAMC and ΔBMC are of equal bases and equal heights.
\(\frac{A(ΔAMC)}{A(ΔBMC)}= \frac{[1]}{[1]}=1\)
Remember :
|
Basic proportionality theorem :
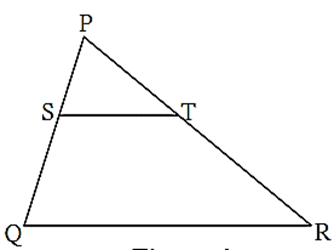
Statement : If a line parallel to a side of a triangle, intersects the remaining sides in two distinct points, then the line divides the sides in the same proportion.
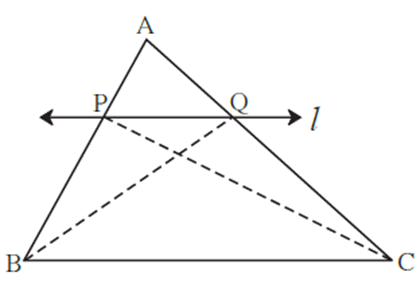
Given : In ΔABC line l || line BC and line l intersects AB and AC in point P and Q respectively
To prove : \(\frac{AP}{PB}=\frac{AQ}{QC}\)
Construction: Draw seg PC and seg BQ
Proof: ΔAPQ and ΔPQB have a common vertex Q and their bases AP and PB lie on the same line AB, they have equal heights.
\(\frac{A(ΔAPQ)}{A(ΔPQB)}= \frac{AP}{PB}\) …..[Triangles of equal heights] (1)
ΔAPQ and ΔPQC have a common vertex P and their bases AQ and QC lie on the same line AC they have equal heights.
\(\frac{A(ΔAPQ)}{A(ΔPQC)}= \frac{AQ}{QC}\) ……[Triangles of equal heights] (2)
ΔPQB and ΔPQC lie between the same two parallel lines PQ and BC, they have equal heights, also they have same base PQ.
A(ΔPQB) = A(ΔPQC) …. [Triangles of same base and equal heights] (3)
from (1), (2) and (3), we get,
\(\frac{A(ΔAPQ)}{A(ΔPQB)}\)=\(\frac{A(ΔAPQ)}{A(ΔPQC)}\) ……(4)
∴ from (1), (2) and (4), we get,
\(\frac{AP}{PB}=\frac{AQ}{QC}\)
Converse of basic proportionality theorem :
Statement : If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
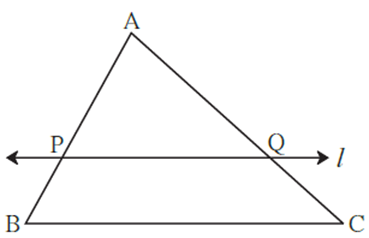
In the figure, line l intersects side AB in point P and side AC in point Q such that A—P—B and A-Q-C.
If \(\frac{AP}{PB}=\frac{AQ}{QC}\) then line l || side BC. OR PQ || side BC
Theorem of an angle bisector of a triangle :
Statement : The bisector of an angle of a triangle divides the side opposite to the angle in the ratio of the remaining sides.
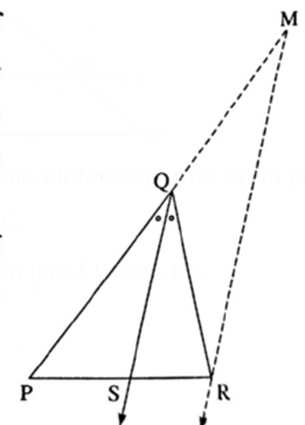
Given : In ΔPQR, bisector of ∠PQR intersects side PR in point S such that P-S-R.
To prove \(\frac{PQ}{QR}=\frac{PS}{PR}\)
Construction: Draw a line parallel to ray QS through point R. Extend seg PQ to intersect the line at point M such that P-Q-M
Proof : In ΔPMR,
seg QS ll side MR ……..(Construction)
∴ by basic proportionality theorem,
\(\frac{PQ}{QM}=\frac{PS}{PR}\) ..... (1)
Ray QS ll side MR and line PM is the transversal.
∴ ∠ PQS ≅ ∠ QMR …………[Corresponding angles] (2)
Ray QS ll side MR and line QR is the transversal.
∴ ∠ SQR ≅ ∠ QRM ………………[Alternate angles] (3)
∠ PQS ≅ ∠ SQR ………[Ray QS is the bisector of ∠ PQR] (4)
In ΔQRM,
∠ QMR ≅ ∠ QRM …….[From (2), (3) and (4)1
∴ seg QR ≅ seg QM ……….[Converse of isosceles triangle theorem] (5)
∴ \(\frac{PQ}{QR}=\frac{PS}{PR}\)………..[From (1) and (5)]
Converse of theorem of an angle bisector of a triangle :
Consider ΔPQR, ray PS intersects side QR in point S such that Q-S-R.
If \(\frac{PQ}{QR}=\frac{PS}{PR}\) then ray PS is the bisector of ∠ QPR.
Another proof of the theorem:
Theorem : The bisector of an angle of a triangle divides the side opposite to the angle in the ratio of the remaining sides.
Given : In ΔABC, seg AD blsects ∠ BAC such that B-D-C.
To prove \(\frac{AB}{AC}=\frac{BD}{DC}\)
Construction : Draw DM ⊥ AB such that A—M—B and and DN ⊥ AC such that A-N-C.
Proof : Point D lies on the bisector of ∠ BAC
By angle bisector theorem, DM = DN …..(1)
Now, the ratio of areas of two triangles is equal to the ratio of the products of their bases and corresponding heights.
∴\(\frac{A(ΔADB)}{A(ΔADC)}= \frac{AB×DM}{AC×DN}\)
∴\(\frac{A(ΔADB)}{A(ΔADC)}= \frac{AB×DM}{AC×DM}\)
∴\(\frac{A(ΔADB)}{A(ΔADC)}= \frac{AB}{AC}\) .....(2)
Also, ΔADB and ΔADC have a common vertex A and their bases BD and DC lie on the same line BC.
∴ their heights are equal.
Areas of triangles with equal heights are proportional to their corresponding bases.
∴\(\frac{A(ΔADB)}{A(ΔADC)}= \frac{BD}{DC}\) .....(3)
from (2) and (3), we get,
\(\frac{AB}{AC}=\frac{BD}{DC}\)
Angle bisector theorem : Every point on the bisector of an angle is equidistant from the sides of the angles.
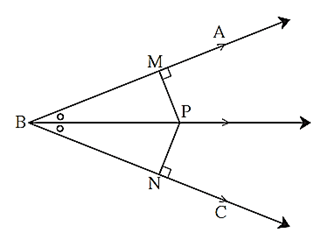
Proof : In the figure, point A lies on the bisector of ∠ ABC and seg PM ⊥ ray BA, and seg PN ⊥ ray BC.
Point P is equidistant from ray BA and ray BC
∴ PM = PN.
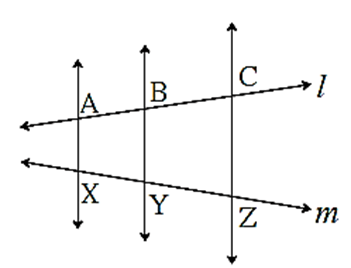
Property of three parallel lines and their transversals :
Statement : The ratio of the intercepts made on a transversal by three parallel lines is equal to the ratio of the corresponding intercepts made on any other transversal by the same parallel lines.
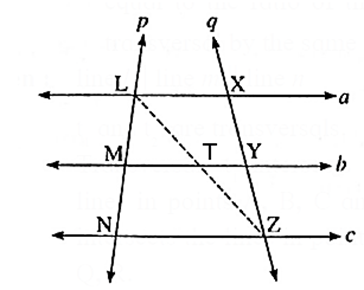
Given : Line a ll line b ll line c. Transversal p intersects lines a, b and c in points L, M and N respectively.
Transversal q intersects lines a, b and c in points
X, Y and Z respectively.
To prove : \(\frac{LM}{MN}=\frac{XY}{YZ}\)
Construction : Draw seg LZ. Let seg LZ intersect seg MY at point T such that M-T-Y and L-T-Z.
Proof: In ΔLNZ, seg MT ll side NZ …….(Given)
∴ by basic proportionality theorem,
\(\frac{LM}{MN}=\frac{LT}{TZ}\)………(1)
In ΔLZX
seg TY || side LX (Given)
∴ by basic proportionality theorem,
\(\frac{LT}{TZ}=\frac{XY}{YZ}\)……..(2)
from (1) and (2),
\(\frac{LM}{MN}=\frac{XY}{YZ}\)
| (1) Basic proportionality theorem.
In ΔABC, if seg PQ || seg AC then \(\frac{AP}{BP}=\frac{QC}{BQ}\) (2) Converse of basic proportionality theorem.
In ΔPQR, if \(\frac{PS}{SQ}=\frac{PT}{TR}\) then seg ST || seg QR. (3) Theorem of bisector of an angle of a triangle.
If in ΔABC, BD is bisector of ∠ ABC, then \(\frac{AB}{BC}=\frac{AD}{DC}\) (4) Property of three parallel lines and their transversals.
If line AX || line BY || line CZ and line l and line m are their transversals then \(\frac{AB}{BC}=\frac{XY}{YZ}\) |
Activity :
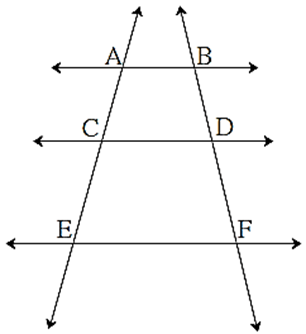
In the figure, AB || CD || EF
If AC = 5.4, CE = 9, BD = 7.5 then find DF
Solution : AB || CD || EF
\(\frac{AC}{[?]}=\frac{[?]}{DF}\) …… ( ???)
\(\frac{5.4}{9}=\frac{[?]}{DF}\)
∴ DF = [ ? ]
AB || CD || EF
\(\frac{AC}{[CE]}=\frac{[BD]}{DF}\) …… ( Property of three parallel lines and their transversals )
\(\frac{5.4}{9}=\frac{[7.5]}{DF}\)
∴ DF = [ 12.5 ]
Activity :
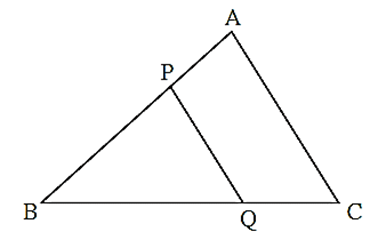
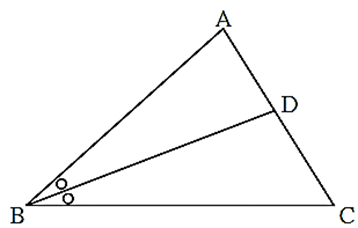
In ΔABC, ray BD bisects ∠ ABC.
A-D-C, side DE || side BC, A-E-B
Then prove that, \(\frac{AB}{BC}=\frac{AE}{BE}\)
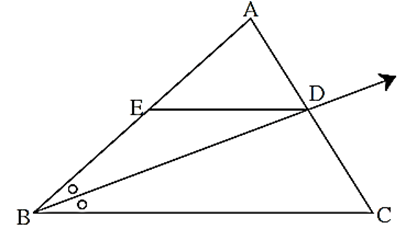
Proof : In Δ ABC, ray BD bisects ∠ B.
∴\(\frac{AB}{BC}=\frac{AD}{DC}\) . . (I) (Angle bisector theorem)
In Δ ABC, DE || BC
\(\frac{AE}{EB}=\frac{AD}{DC}\) . . . . . (II) (????)
\(\frac{AB}{[?]}=\frac{[?]}{EB}\) . . . . . . from (I) and (II)
Proof : In Δ ABC, ray BD bisects ∠ B.
∴\(\frac{AB}{BC}=\frac{AD}{DC}\) . . (I) (Angle bisector theorem)
In ΔABC, DE || BC
\(\frac{AE}{EB}=\frac{AD}{DC}\) . . . . . (II) (Basic proportionality theorem )
\(\frac{AB}{[BC]}=\frac{[AE]}{EB}\) . . . . . . from (I) and (II)
| Similar figures : Figures which are of same shape but may be of different sizes are called similar figures.
It means similar figures are always of same shape but can be of different sizes. If similar figures are of same shape and size then those figures are also congruent. |
| Similar triangles : For a given one to one correspondence between the vertices of two triangles, if
(i) their corresponding angles are congruent and, (ii) their corresponding sides are in same proportion, then the correspondence is known as similarity and the two triangles are said to be similar triangles.
In ΔABC and ΔDEF, if ∠ A ≅ ∠ D, ∠ B ≅ ∠ E, ∠ C ≅ ∠ F and \(\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}\) then ΔABC and ΔDEF are similar triangles. |
Test of similarity of triangles :
To prove two triangles similar, it is not necessary that We need to prove all pairs of corresponding angles congruent and corresponding sides in proportion. Similarity of triangles can be confirmed by testing three specific conditions, often referred as ‘Tests of similarity‘.
When three specific conditions are fulfilled, the remaining conditions are also fulfilled. There are three tests of similarity of triangles.
- AAA test of similarity or AA test of similarity
- SAS test of similarity
- SSS test of similarity.
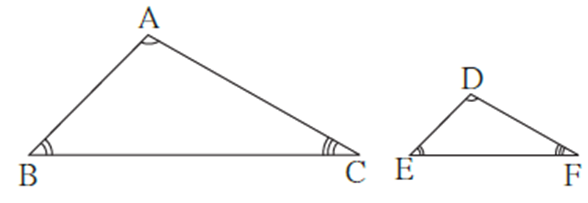
(1) AAA test : For a given one-to-one correspondence between the vertices of two triangles, if the corresponding angles are congruent, then the two triangles are similar.
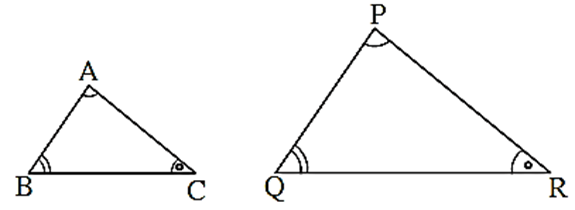
In ΔABC and ΔPQR, in the correspondence ABC ↔ PQR if
∠ A ≅ ∠ P, ∠ B ≅ ∠ Q and ∠ C ≅ ∠ R
then by AAA test ΔABC ∼ ΔPQR.
AA test : For a given one-to-one correspondence between the vertices of two triangles, if two angles of one triangle are congruent with the corresponding two angles of the other triangle, then the two triangles are similar.
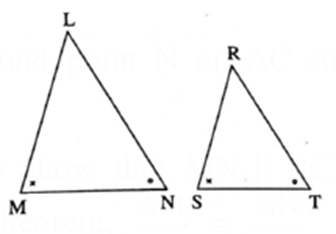
In the figures, under the correspondence
LMN ↔ RST,
∠ M ≅ ∠ S, ∠ N ≅ ∠ T.
Then by AA test,
ΔLMN ∼ ΔRST.
(2) SAS test : For a given one-to-one correspondence between the vertices of two triangles, if two sides of one triangle are proportional to the corresponding sides of the other triangle and the angles included by them are congruent, then the two triangles are similar.
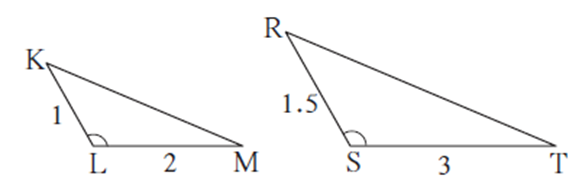
Example :
if in ΔKLM and ΔRST,
\(\frac{KL}{RS}=\frac{1}{1.5}=\frac{1×2}{1.5×2}=\frac{2}{3}\)
\(\frac{LM}{ST}=\frac{2}{3}\)
∴ \(\frac{LL}{RS}=\frac{LM}{ST}=\frac{2}{3}\) and ∠ KLM ≅ ∠ RST
Therefore, by SAS test ΔKLM ∼ ΔRST
(3) SSS test : For a given one-to-one correspondence between the vertices of two triangles, if three sides of one triangle are proportional to the three corresponding sides of the other triangle, then the two triangles are similar.
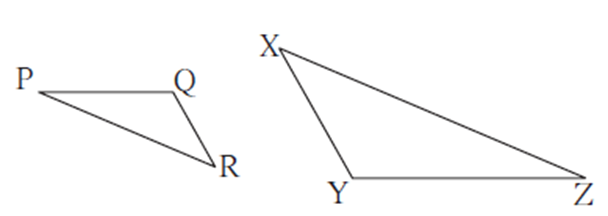
Example: if in ΔPQR and ΔXYZ,
If \(\frac{PQ}{ZY}=\frac{QR}{YX}=\frac{PR}{ZX}\)
then by SSS test DPQR ∼ DZYX
Properties of similar triangles :
(1) ΔABC ∼ ΔABC –Reflexivity : Every triangle is similar to itself.
(2) If ΔABC ∼ ΔDEF then ΔDEF ∼ ΔABC – Symmetry : If one triangle is similar to a second triangle, then the second triangle is similar to thefirst.
(3) If ΔABC ∼ ΔDEF and ΔDEF ∼ ΔGHI, then ΔABC ∼ ΔGHI – Transitivity: If one triangle is similar to a second triangle and the second triangle is similar to a third triangle, then the first triangle is similar to the third triangle.
Proof of AAA test:
Given : In ΔPQR and ΔXYZ, ∠ P ≅ ∠ X, ∠ Q ≅ ∠ Y and ∠ R ≅ ∠ Z.
To prove : ΔPQR ∼ ΔXYZ
Proof : Let us consider ΔPQR bigger than ΔXYZ. Mark a point S on side PQ such that XY = PS and P—S—Q. Mark a point T on side PR such that XZ = PT and P—T—R. In ΔSPT and ΔYXZ, seg PS ≅ seg XY (Construction) ∠ SPT ≅ ∠ YXZ (Given) seg PT ≅ seg XZ (Construction) ΔSPT ≅ ΔYXZ (SAS test) ∠ PST ≅ ∠ XYZ (c.a.c.t.) as ∠ XYZ ≅ ∠ PQR (Given) ∠ PST ≅ ∠ PQR seg ST || side QR ….. (Corresponding angles test for parallel lines) ∴ \(\frac{PS}{SQ}=\frac{PT}{TR}\) …….(By basic proportionality theorem) By invertendo, \(\frac{SQ}{PS}=\frac{TR}{PT}\) By componendo, \(\frac{SQ+PS}{PS}=\frac{TR+PT}{PT}\) ∴ \(\frac{PQ}{PS}=\frac{PR}{PT}\) ∴ \(\frac{PQ}{XY}=\frac{PR}{XZ}\)…..(‘.’ PS = XY and PT = XZ, construction) … (1) Similarly, we can prove \(\frac{PQ}{XY}=\frac{QR}{YZ}\) …. (2) ∴ \(\frac{PQ}{XY}=\frac{QR}{YZ}=\frac{PR}{XZ}\)…..[ from (1) and (2)]…..(3) Thus for ΔPQR and ΔXYZ, ∠ P ≅ ∠ X, ∠ Q ≅ ∠ Y and ∠ R ≅ ∠ Z. ….(Given) And \(\frac{PQ}{XY}=\frac{QR}{YZ}=\frac{PR}{XZ}\) ……[From (3)] ∴ ΔPQR ∼ ΔXYZ.
Text Book Example 4 :
In the adjoining figure BP ⊥ AC, CQ ⊥ AB, A–P–C, A–Q–B , then prove that ΔAPB and ΔAQC are similar.
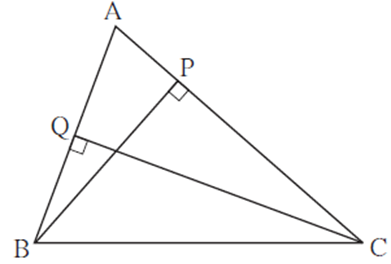
Solution : In ΔAPB and ΔAQC
∠ APB = [ ? ]° ….(I)
∠ AQC = [ ? ]° …..(II)
∴ ∠ APB ≅ ∠ AQC ....from (I) and (II)
∠ PAB ≅ ∠ QAC .... [(???)]
∴ ΔAPB ∼ ΔAQC ..... AA test
Solution : In ΔAPB and ΔAQC ∠ APB = [ 90 ]° ….(I) ∠ AQC = [ 90 ]° …..(II) ∴ ∠ APB ≅ ∠ AQC ....from (I) and (II) ∠ PAB ≅ ∠ QAC .... [(common angle)] ∴ ΔAPB ∼ ΔAQC ..... AA test
Theorem of areas of similar triangles :
Theorem : When two triangles are similar, the ratio of areas of those triangles is equal to the ratio of the squares of their corresponding sides.
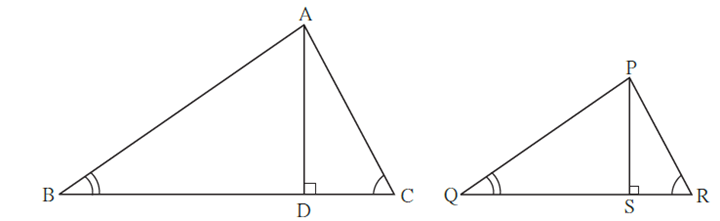
Given : ΔABC ∼ ΔPQR
To prove : \(\frac{A(ΔABC)}{A(ΔPQR)}=\frac{AB^2}{PQ^2}=\frac{BC^2}{QR^2}=\frac{AC^2}{PR^2}\)
Construction : Draw‘ seg AD ⊥. side BC such that B—D—C and seg PS ⊥ side QR such that Q—S—R.
Proof : Ratio of areas of two triangles is equal to the ratio of the products of their bases and corresponding heights. ∴ \(\frac{A(ΔABC)}{A(ΔPQR)}=\frac{BC×AD}{QR×PS}\) ∴ \(\frac{A(ΔABC)}{A(ΔPQR)}=\frac{BC}{QR}×\frac{AD}{PS}\) ….(1) ΔABC ∼ ΔPQR ….. (Given) ∠ B ≅ ∠ Q …….(Corresponding angles of similar triangles are congruent) …(2) and \(\frac{AB}{PQ}=\frac{BC}{QR}=\frac{AC}{PR}\)…(Corresponding sides of similar triangles are in proportion)..(3) In ΔABD and ΔPQS, ∠ ABD ≅ ∠ PQS …..[From (2)] ∠ ADB ≅ ∠ PSQ (Each measures 90°) ∴ΔABD ∼ ΔPQS ……(AA test of similarity) ∴ \(\frac{AB}{PQ}=\frac{AD}{PS}\) …..(Corresponding sides of similar triangles are in proportion)…(4) from (3) and (4), we get, \(\frac{AB}{PQ}=\frac{BC}{QR}=\frac{AD}{PS}\) ∴ \(\frac{BC}{QR}=\frac{AD}{PS}\) ….(5) ∴ \(\frac{A(ΔABC)}{A(ΔPQR)}=\frac{BC}{QR}×\frac{BC}{QR}=\frac{BC^2}{QR^2}\) …..[from (1) and (5)]….(6) \(\frac{A(ΔABC)}{A(ΔPQR)}=\frac{AB^2}{PQ^2}=\frac{BC^2}{QR^2}=\frac{AC^2}{PR^2}\) ……from (1) and (6)
PDF
Visit Kitabcd PDF store https://test.kitabcd.org/shop/