Notes-Class-10-Mathematics-1-Chapter-2-Quadratic Equations-Maharashtra Board

Topics to be learn : Quadratic Equations : Introduction Methods of Solving Quadratic Equations Nature of the Roots of Quadratic Equation Relation Between the Roots and the Coefficients Application of Quadratic Equations

Quadratic Equations : Introduction

Linear and quadratic polynomial : When the degree of polynomial is 1 it is called a linear polynomial and if degree of a polynomial is 2 it is called a quadratic polynomial.

Quadratic equation : The equation obtained by taking the value of a quadratic polynomial zero, is called a quadratic equation.

Examples :

In the following given polynomials

5x + 9, x² + 3x −5, 3x − 7, 3x² − 5x, 5x²

• 5x + 9 and 3x – 7 are linear polynomial
• x² + 3x −5, 3x² − 5x, and 5x² are quadratic polynomial
• x² + 3x −5 = 0, 3x² − 5x = 0, and 5x² = 0 are quadratic equations formed by taking the value of the quadratic polynomials zero.

In above equations

• Coefficients of x² are 1, 3 and 5 these coefficients are non zero.
• Coefficients of x are 3, −5 and 0
• Constants terms are −5, 0 and 0
• Here constant term of second and third polynomial is zero.

 Standard form of quadratic equation :

The equation involving one variable and having the maximum index of the variable 2 is called a quadratic equation.

• The equation ax² + bx + c = 0 is called the standard or general form of quadratic equation. Here, a, b and c are real numbers and a ≠
• In the equation ax² + bx + c = 0, if b = 0, then the equation becomes ax² + c = 0. This is also a quadratic equation.
• Similarly, if c = 0, then ax² + bx = 0 is a quadratic equation.
• If b = 0 and c = 0, then ax² = 0 is a quadratic equation.

In the quadratic equation ax² + bx + c = 0, the constants a, b, c are called the quadratic coefficient, the linear coefficient and the constant term respectively.

Examples:

(1) Complete the following table

Quadratic equation	general form	a	b	c
x2 − 4 = 0	x2 − 0x − 4 = 0	1	0	−4
y2 = 2y − 7	y2 − 2y + 7 = 0	1	−2	7
x2 + 2x = 0	x2 + 2x +0 = 0	1	2	0

(2) Decide which of the following are quadratic equations ?

(1) 3x² − 5x + 3 = 0 (2) 9y² + 5= 0 (3) m³ − 5m² + 4 = 0 (4) (l + 2) (l − 5) = 0

Solution :

(1) In the equation 3x² − 5x + 3 = 0, x is the only variable and maximum index of the variable is 2, ∴ It is a quadratic equation.

(2) In the equation 9y² + 5= 0, y is the only variable and maximum index of the variable is 2, ∴ It is a quadratic equation.

(3) In the equation m³ − 5m² + 4 = 0, m is the only variable but maximum index of the variable is not 2. ∴ It is not a quadratic equation.

(4) Simplifying equation (l + 2) (l − 5) = 0

∴ l (l − 5) + 2 (l − 5) = 0

∴ l² − 5l + 2l − 10 = 0

∴ l² − 3l − 10 = 0, In this equation l is the only variable and maximum index of the variable is 2. ∴ It is a quadratic equation.

Roots of a quadratic equation :

The values of the variable which satisfy the given quadratic equation are called the solutions or the roots of the quadratic equation.

Examples:

(1) Let put x = −6 in the polynomial x² + 5x − 6

x² + 5x − 6 = (−6)² + 5 × (−6) − 6

= 36 − 30 − 6 = 0

∴ x = −6 is a solution of the equation.

Hence −6 is one root of the equation x² + 5x − 6 = 0

(2) 2x² − 7x + 6 = 0 check whether (i) x = \(\frac{3}{2}\)  , (ii) x = −2 are solutions of the equations.

Solution :

 (i) Put x = \(\frac{3}{2}\)  in the polynomial 2x² − 7x + 6

2x² − 7x + 6 =  \(2(\frac{3}{2})^2-7(\frac{3}{2})+6\)

= \(2×\frac{9}{4}-\frac{21}{2}+6\)

= \(\frac{9}{2}-\frac{21}{2}+\frac{12}{2}\) = \(\frac{9-21+12}{2}=0\)

∴ \(\frac{3}{2}\) is a solution of the equation.

(ii) Let put x = −2 in 2x² − 7x +6

2x² − 7x + 6 = 2(−2)² − 7(−2) + 6

= 2 × 4 + 14 + 6

= 8 + 14 +6 = 28 ≠ 0

∴ x = −2 is not a solution of the equation.

(3) If x = 5 is a root of equation kx² − 14x − 5 = 0 then find the value of k by completing the following activity.

Solution :

One of the roots of equation kx² − 14x − 5 = 0 is 5.

∴ Now Let substitute  x = 5 in the equation.

∴ k(5)² – 14(5) − 5 = 0

∴  25k − 70 − 5 = 0

25k – 75 = 0

25k = 75

∴ k = \(\frac{75}{25}\) = 3

Remember :

• ax² + bx + c = 0 is the general form of equation where a, b, c are real numbers and ’a ’ is non zero.
• The values of variable which satisfy the equation are called solutions or roots of the equation.

Let’s Recall : Find the factors of the following polynomials.

(i) x² − 4 x −5, (ii)  2m² − 5 m (iii) a² − 25

Answer :

(i) x2 − 4 x −5, =  x2 − 5 x + 1x −5 = x(x – 5) + 1(x – 5) = (x + 1)(x – 5)

(ii)  2m2 − 5 m = m(2m – 5)

(iii) a2 − 25 = (a)2 – (5)2 = (a + 5)(a – 5)

Methods of Solving Quadratic Equations are : Factorisation method, Completing square method and Formula method.

Solutions of a quadratic equation by factorisation :

Factorisation method :

• Write the given equation in the form ax² + bx + c = 0
• Find the two linear factors of the LHS of the equation
• Equate each linear factor to zero.
• Solve each equation obtained in 3 and write the roots of the given equation.

Examples :

(1) Solve the quadratic equation x² + 8x + 15 = 0 by factorisation method :

Step 1 : Split the middle term 8x as 3x and 5x. [Because 3x × 5x = 15x² = x² × 15.]

x² + 5x+ 3x + 15 = 0

Step 2 : Find the factors of LHS

x(x + 3) + 5(x + 3) = 0

(x + 5)(x + 3) = 0

Step 3 : If the product of two numbers is zero, then at least one of them must be zero.

x + 3 = 0  or x + 5 = 0

Step 4 : Solve each linear equation.

x = −3  or x = −5

Step 5 : Write the answer.

The roots of the equation are −3, −5

(2) Solve the following quadratic equations by factorisation.

(i) m² − 14 m + 13 = 0, (ii) 3x² − x − 10 = 0 , (iii) 3y² = 15 y, (iv) x² = 3,

(v) 6\(\sqrt{3}\)x² + 7x = \(\sqrt{3}\)

Remember : While solving quadratic equation ax² + bx + c , the coefficient of x² i.e ‘a’ required to multiply by constant  ‘c’ for factorisation

Solution of a quadratic equation by completing the square :

The quadratic equation of the type x² + 10x + 2 = 0 cannot be solved by the method of factorisation, because we cannot find two factors of 2 whose sum is 10.

In such a case, completing square method is used for solving quadratic equations.

For solving quadratic equation by this method proceed as follows :

Step 1 : Write the given equation in the form ax² + bx + c = 0

x² + 10x + 2 = 0

Step 2 : Considering the first two terms on LHS, find the third suitable square term to make the polynomial a perfect square.

Lets add a suitable term in first two LHS terms i.e. k

x² + 10x + k = (x + a)²

then x² + 10x + k = x² + 2ax + a²

∴ 10 = 2a and k = a²

∴ a = 5,  ∴ k = a² = (5)² = 25

Step 3 :  Add the square term and subtract the same.

x² + 10x + 25 – 25 + 2 = 0

Step 4 :  Write the square of the first three terms and the last two terms.

(x + 5)² − 25 + 2 = (x + 5)² – 23 = (x + 5)² – (\(\sqrt{23}\))²

∴ (x + 5)² – (\(\sqrt{3}\))² = 0

Step 5 :  Factorise and equate each factor to zero.

∴ (x + 5 + \(\sqrt{3}\) )(x + 5 − \(\sqrt{3}\) ) = 0

∴ x + 5 + \(\sqrt{3}\) = 0 or x + 5 − \(\sqrt{3}\) = 0

Step 6 :  Find the value of x

∴ x = − 5 − \(\sqrt{3}\) or x = − 5 + \(\sqrt{3}\)

∴ − 5 − \(\sqrt{3}\) ,  − 5 + \(\sqrt{3}\) are the roots of the quadratic equation

Recall formulae : (a + b)2 = a2 + 2ab + b2 (a2 – b2) = (a + b)(a – b)

Examples :

(1) Solve : 5x² − 4x − 3 = 0

(2) Solve : x² + 8x − 48 = 0

Formula for solving a quadratic equation :

ax² + bx + c, Divide the polynomial by a ( ‘.’ a ≠ 0) to get x² + \(\frac{b}{a}\)x + \(\frac{c}{a}\).

Let us write the polynomial x² + \(\frac{b}{a}\)x +  \(\frac{c}{a}\) in the form of difference of two square numbers. Now we can obtain roots or solutions of equation x² +  x +  = 0 which is equivalent to ax² + bx + c = 0 .

ax² + bx + c = 0  

x² + \(\frac{b}{a}\)x + \(\frac{c}{a}\)  .....dividing both sides by a

∴ x² + \(\frac{b}{a}\)x + \((\frac{b}{2a})^2\) − \((\frac{b}{2a})^2\) + \(\frac{c}{a}\)  = 0   

∴ \((x +\frac{b}{2a})^2\) − \(\frac{b^2}{4a^2}\) + \(\frac{c}{a}\) = 0

∴ \((x +\frac{b}{2a})^2\) − \(\frac{b^2-4ac}{4a^2}\) = 0

∴ \((x +\frac{b}{2a})^2\) = \(\frac{b^2-4ac}{4a^2}\)

∴ \(x +\frac{b}{2a}\) = \(\sqrt{\frac{b^2-4ac}{4a^2}}\)  or \(x +\frac{b}{2a}\) = \(-\sqrt{\frac{b^2-4ac}{4a^2}}\) 

∴ \(x=-\frac{b}{2a}+\sqrt{\frac{b^2-4ac}{4a^2}}\)  or \(x=-\frac{b}{2a}-\sqrt{\frac{b^2-4ac}{4a^2}}\)

∴ \(x=\frac{-b+\sqrt{b^2-4ac}}{2a}\) or \(x=\frac{-b-\sqrt{b^2-4ac}}{2a}\)

In short the solution is written as \(x=\frac{-b±\sqrt{b^2-4ac}}{2a}\)

  and these values are denoted by α,  β.

∴  \(α=\frac{-b+\sqrt{b^2-4ac}}{2a}\)  , \(β=\frac{-b-\sqrt{b^2-4ac}}{2a}\)        .....(1)

The values of a, b, c from equation ax² + bx + c = 0  are substituted in \(\frac{-b±\sqrt{b^2-4ac}}{2a}\) and further simplified to obtain the roots of the equation.

So \(x=\frac{-b±\sqrt{b^2-4ac}}{2a}\)  is the formula used to solve quadratic equation. Out of the two

roots any one can be represented by α and the other by β.

That is, instead (I) we can write

\(α=\frac{-b+\sqrt{b^2-4ac}}{2a}\)  , \(β=\frac{-b-\sqrt{b^2-4ac}}{2a}\)      .....(2)

Note that : If \(α=\frac{-b+\sqrt{b^2-4ac}}{2a}\)  then α > β

If \(α=\frac{-b-\sqrt{b^2-4ac}}{2a}\)  then α < β

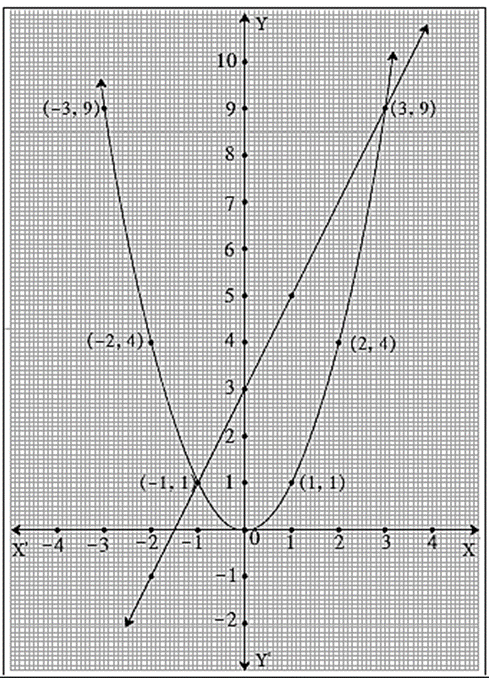
For more information : Solve the quadratic equation x2 − 2x −3 = 0 graphically x2 − 2x −3 = 0  ∴ x2 = 2x + 3 Let y = x2 = 2x + 3 . Let us draw graph of y = x2 and y = 2x + 3 y = x2 x 3 2 1 0 −1 −2 −3 y 9 4 1 0 1 4 9 y = 2x + 3 x −1 0 1 −2 y 1 3 5 −1 The graph of y = x2 is a parabola. The graphs of y = x2 and y = 2x + 3 intersect each other at (−1, 1) and (3, 9).  ∴ x = −1 or x = 3 is the solution of the given quadratic equation.

Solve the equation 2x² + 13x + 15 = 0 by

(i) factorisation method

(ii) completing the square method

(iii) using formula. '

Verify that you will get the same roots every time.

 Nature of roots of a quadratic equation :

The roots of quadratic equation ax² + bx + c = 0 are \(x=\frac{-b±\sqrt{b^2-4ac}}{2a}\)

(1) If b²− 4ac = 0 then, \(x=\frac{-b±\sqrt{0}}{2a}\)

∴ \(x=\frac{-b+0}{2a}\) or  \(x=\frac{-b-0}{2a}\)

∴ the roots of the quadratic equation are real and equal.

(1) If b² − 4ac > 0 then, \(x=\frac{-b±\sqrt{b^2-4ac}}{2a}\)

∴ \(x=\frac{-b+\sqrt{b^2-4ac}}{2a}\)  , \(x=\frac{-b-\sqrt{b^2-4ac}}{2a}\)

∴ the roots of the quadratic equation are real and unequal.

(1) If b² − 4ac < 0 then, \(x=\frac{-b±\sqrt{b^2-4ac}}{2a}\) are not real numbers

∴ the roots of quadratic equations are not real.

[b² − 4ac < 0  the value of b² − 4ac is negative. The root of a negative number is not real.]

• The roots of the quadratic equation ax² + bx + c = 0 are determined by the value of b² − 4ac.
• Hence, b² − 4ac is called the discriminant of the quadratic equation. It is denoted by Δ (Delta, a Greek letter).

Example :

(i) Fill in the blanks.

Value of discriminant	Nature of roots
50	real and unequal
−30	not real
0	real and equal

(ii) Determine nature of roots of the quadratic equations.  2x² − 5x + 7 = 0

Solution : Compare 2x² − 5x + 7 = 0 with

ax² + bx + c = 0

a = 2, b = −5 , c = 7 ,

∴ b² − 4 ac = (−5)² − 4 × 2 × 7

D = 25 − 56

D = −31

∴ b² − 4 ac < 0

∴ the roots of the equation are not real.

The relation between roots of the quadratic equation and coefficients :

The roots of quadratic equation ax² + bx + c = 0 are α and  β then.

  \(α=\frac{-b+\sqrt{b^2-4ac}}{2a}\)  and   \(β=\frac{-b-\sqrt{b^2-4ac}}{2a}\)         .....(1)

α +  β = \(\frac{-b+\sqrt{b^2-4ac}}{2a}\)+\(\frac{-b-\sqrt{b^2-4ac}}{2a}\) = \(-\frac{2b}{2a}\)

           = \(-\frac{b}{a}\)

The sum of the roots = \(-\frac{b}{a}\) = \(-\frac{coefficient\,\, of\,\,x}{coefficient\,\, of\,\,x^2}\)

α ×  β = \(\frac{-b+\sqrt{b^2-4ac}}{2a}\)×\(\frac{-b-\sqrt{b^2-4ac}}{2a}\)

            = \(\frac{(-b)^2-(\sqrt{b^2-4ac})^2}{4a^2}\)

           = \(\frac{b^2-b^2+4ac}{4a^2}\)

           = \(\frac{c}{a}\) 

The product of the roots = \(\frac{c}{a}\) = \(-\frac{constant\,\,term}{coefficient\,\, of\,\,x^2}\)

Note : If α = 1 α +  β = −b and α ×  β = c

Example :

Find α +  β and α ×  β for 10x² + 10x + 1 = 0,

Answer :  α +  β = \(-\frac{b}{a}=-\frac{10}{10}\) =  −1

and α ×  β = \(\frac{c}{a}=\frac{1}{10}\)

To obtain a quadratic equation having given roots

If α and β be the roots of a quadratic equation in variable x then  x = α and x = β

∴ x - α = 0 or x - β = 0

∴ (x - α)(x - β) = 0

∴ x² - (α + β) x + α β = 0

When two roots of equation are given then quadratic equation can be obtained as

x² - (addition of roots)x + product of the roots = 0.

Example :

(1) Write the quadratic equation if addition of the roots is 10 and product of the roots = 9

Answer :

Quadratic equation : x² - (addition of roots)x + product of the roots = 0.

                               = x² - (10)x + 9 = 0.

(2) What will be the quadratic equation if α = 2, β = 5

Solution :

It can be written as x² - (α + β) x + α β = 0

∴ x² - (2 + 5) x + 2×5 = 0

∴ x² - 7x + 10 = 0

(3) Obtain the quadratic equation if roots are -3, -7.

Solution : Let α = -3 and β = -7

∴ α + β = (-3) + (-7) = -10 and α × β = (-3) × (-7) = 21

∴ and quadratic equation is, x² - (α + β) x + α β = 0

∴ x² -(-10) x + 21 = 0

∴ x² + 10x + 21 = 0

Remember : (1) The roots of quadratic equation ax2 + bx + c = 0 are α and  β then. \(α=\frac{-b+\sqrt{b^2-4ac}}{2a}\)  and \(β=\frac{-b-\sqrt{b^2-4ac}}{2a}\)       α +  β = \(-\frac{b}{a}\) α ×  β =   \(\frac{c}{a}\) (2) The roots of the quadratic equation ax2 + bx + c = 0 are determined by the value of b2 − 4ac. Hence, b2 − 4ac is called the discriminant of the quadratic equation. It is denoted by Δ (Delta, a Greek letter). (3) If Δ = 0 The roots of quadratic equation are real and equal. If Δ > 0 then the roots of quadratic equation are real and unequal. If Δ < 0 then the roots of quadratic equation are not real. (4) If α and β be the roots of a quadratic equation then x2 - (α + β) x + α β = 0

Application of quadratic equation :

Quadratic equations are useful to solve problems arising in our day-to-day life.

The method of solving problems consists of the following three steps :

• Step 1 : Convert the word problem, into symbolic language, i.e. form mathematical equation by identifying the relationship existing in the problem.
• Step 2 : Solve the quadratic equation thus formed.
• Step 3 : Interpret the solution of the equation into verbal language. The appropriate solution/ solutions satisfying the given conditions is/ are to be considered.

Example :

(1) There is a rectangular onion storehouse in the farm of Mr. Ratnakarrao at Tivasa. The length of rectangular base is more than its breadth by 7 m and diagonal is more than length by 1 m. Find length and breadth of the storehouse.