Nuclear Chemistry and Radioactivity
Maharashtra State Board-Class-11-Science-Chemistry-Chapter -13
|
Topics to be Learn :
|
Introduction :
Nuclear chemistry : It is a branch of physical chemistry and it deals with the study of reactions involving the changes in atomic nuclei.
Examples of nuclear reactions are :
- radioactive decay
- artificial transmutation
- nuclear fission
- nuclear fusion.
Similarity between solar system and structure of atom :
The sun is the center of the solar system, and planets revolve it using gravity. This is equivalent to atomic structure, where the nucleus is at the center and electrons rotate around it.
Atom : An atom consists of tiny central core called nucleus consisting of protons and neutrons and the surrounding space is occupied by fast moving electrons.
- The radius of nucleus is of the order of 10—15 m while atomic radius is of the order of 10—10 Hence, the size of outer sphere of an atom is 105 times larger than the nucleus.
- If compare atom size with nucleus size: The nucleus in the center of the atom would be the size of a pea if the atom were the size of a football stadium.
- Composition of an atom or element is denoted as \(_Z^AX\) where X is the symbol of the element. Z equals number of protons and is called atomic number of the element. ‘A' is the mass number or the sum of number of protons and neutrons in an atom.
Atomic number (Z) : It is equal to number of protons present in the nucleus of an atom (or it represents total number of electrons in an atom.)
Mass number (A) : This represents the sum of protons and neutrons or total number of nucleous present in the nucleus of an atom.
∴ A = Z + N
where N is number of neutrons present in the nucleus of an atom.
Radius of nucleus related to mass number :
The radius (R) of the nucleus is given by,
R = RO A1/3
where A is mass number of an atom, RO is constant, common to all nuclei, and
RO = 1.33 x 10—15 m
Classification of nuclides
Nuclide : The nucleus of a specific isotope or an atom is called nuclide.
Classification on the basis of number of nucleons :
On the basis of number of neutrons and protons nuclides are classified as follows :
(i) Isotopes : The nuclides (or atoms) which have the same number of protons but different number of neutrons are called isotopes. OR Atoms having same atomic number but different mass number are called isotopes.
For example, \(_{11}^{22}\)Na, \(_{11}^{23}\)Na and \(_{11}^{24}\)Na, \(_{17}^{38}\)Cl and \(_{17}^{35}\)Cl
(ii) Isobars : The nuclides (or atoms) which have the same mass number and different atomic number or same number of protons and neutrons are called isobars.
For example, \(_{6}^{14}\)C and \(_{7}^{14}\)N,
(iii) Mirror nuclei : These are isobars in which the number of protons and neutrons differ by 1 and are interchanged. For example, H and He, C and N
(iv) Isotones : These are nuclides (or atoms) having same number of neutrons but different number of protons and different mass numbers.
For example, \(_{6}^{13}\)C and \(_{7}^{14}\)N, \(_{16}^{32}\)S and \(_{15}^{31}\)P,
(v) Nuclear isomers : These are nuclides having the same number of protons (Z) and neutrons (N) or the same mass number (A) but differ in energy states.
For example, \(_{27}^{60m}\)Co and \(_{27}^{60}\)Co. The isomer of higher energy is said to be in the meta stable state indicated by writing ‘m’ after the mass number.
Classification on the basis of nuclear stability :
On the basis of nuclear stability, nuclides are classified as :
(i) Stable nuclides : In these nuclides, the number of protons and neutrons and their nuclear properties remain unchanged.
(ii) Unstable or radioactive nuclides : These nuclides undergo spontaneous disintegration forming new nuclides.
Nuclear stability :
Even-odd nature of proton number (Z) and neutrons (N) :
Nuclear stability on the basis of even-odd of protons and neutrons :
- Nuclides with even Z and even N are very stable. They tend to form proton-proton and neutron-neutron pairs which imparts the stability to the nucleus. Nearly 85% of earth crust contains nuclides with even Z and even N i.e., even number of protons and even number of neutrons.
For example, \(_{2}^{4}\)He, \(_{8}^{16}\)O, \(_{20}^{40}\)Ca, etc.
- There is one-third number of stable nuclides with either Z or N odd compared to both are even. But these nuclides are less stable compared to even number of protons and neutrons. This is due to the absence of a partner nucleon for pairing of one nucleon. Nucleon pairing does not take place between proton and neutron. The nuclides with odd A are nearly the same irrespective of Z or N is odd. This suggest that protons and neutrons behave similar way with respect to the stability.
- There are only four stable nuclides with odd Z and odd N. Generally they are unstable due to the presence of two unpaired nucleous and about 2% of the earth’s crust consists of such nuclides.
Neutron to Proton ratio (N/Z) :
The nuclear stability can be explained with the help of neutrons to proton (N/Z) ratio.
- When for stable nuclides the number of neutrons (N) is plotted as a function of number of protons (Z), a curve is obtained. This curved belt is called nuclear stability zone.
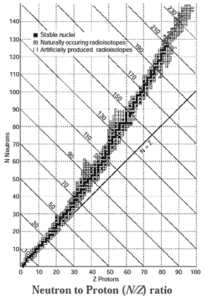
- The nuclides which exist outside the stability zone are unstable and radioactive.
- A straight line below the belt has equal number of neutrons and protons or the slope N/Z =1.
- Nuclides lighter than \(_{20}^{40}\)Ca are stable and have N = Z.
- For stable nuclides heavier than calcium, the ratio N/Z is greater than one.
- In heavier nuclides with the increasing number of protons there arises large coulombic repulsion among them. With increased number of neutrons the protons in the nuclei get separated decreasing the repulsion and increasing stability. Therefore, heavier nuclides require more number of neutrons than protons to attain a stability.
Magic numbers : The nuclei with 2, 8, 20, 28, 50, 82 and 126 neutrons or protons are particularly stable and abundant in nature. These are magic numbers.
For example, Lead ( \(_{82}^{208}\)Pb ) has two magic numbers, 82 protons and 126 neutrons.
The most stable nuclide known is \(_{26}^{56}\)Fe. It has two magic numbers namely 26 protons and 56 - 26 = 30 neutrons. They have even Z and N. This gives extra stability to the nuclide.
Nuclear Potential :
Nuclear potential and its consequences :
- In the nucleus, there are positively charged protons. The distance between two protons is about 10—15 m, hence, the repulsion between them is extremely large.
- There are nuclear forces of attraction between all the nucleons namely protons and neutrons holding them together. These arise due to attraction between proton-proton (p-p), neutron-neutron (n-n) and proton-neutron (p-n).
- These forces are independent of charge of nucleons and they are equal and operate over short range in the nucleus.
- Nuclear potential : The p-p, n-n and p-n attractions constitute what is called the nuclear potential and the consequences of this is nuclear stability.
Nuclear binding energy and mass defect :
Nuclear binding energy : The energy released equivalent to the mass lost (defect) during the formation of an atom (or nuclide) is called nuclear binding energy.
Mass defect : The difference between (theoretically) calculated mass and the observed mass of an atom (or on isotope) is called the mass defect.
Mass defect = Δm = Calculated mass — Observed mass
Units of nuclear masses and energy : The nuclear mass is usually expressed in unified mass unit (u) which is exactly 1/12th of the mass of 12C atom.
Thus, 1u = 1/12th mass of C-12 atom = 1.66 x 10-27 kg.
The energy released (in Joules) in the conversion of 1 u mass into energy is given by the expression :
E = mc2 = (1.66 x 10-27kg) x (3 x 108m s-1)2
Expression for nuclear binding energy :
Consider a nuclide, \(_{Z}^{A}\)X containing Z protons, Z electrons and (A — Z) neutrons.
If the masses of proton, electron and neutron are mp, me and mn respectively then, theoretical total mass of nuclide is,
Total mass = Z x mp + Z x me + (A — Z) x mn
If m is the observed mass of the nuclide then,
Mass defect = Total mass — Observed mass
Δm = [Z x mp + Z x me + (A — Z) x mn] — m
= [Z (mp + me) + (A — Z) x mn] — m
Since the mass of one H atom is,
mH = mp + me
Δm = [Z x mH + (A — Z) x mn] — m
Since the energy obtained from the loss of 1 u mass is 931.4 MeV,
Total binding energy = Δm x 931.4 MeV
B.E. = [Z x mH + (A — Z) x mn — m] x 931.4 MeV
Since there are A number of nucleons (protons and neutrons),
Binding energy per nucleon = \(\bar{B}\) = \(\frac{Δm×931.4}{A}\)
Binding energy per nucleon = \(\bar{B}\) = \(\frac{[Z×m_H+(A-Z)×m_n-m]×931.4}{A}\)MeV
Binding energy curve :
The nuclear stability can be explained by plotting binding energy per nucleon as a function of mass number A of various nuclides. The parabolic curve obtained is called binding energy curve.

Inferences from binding energy curve :
- Light nuclides (A < 30) : For light nuclides, the peaks in curve with A values in multiples of 4 are very stable. They are \(_{2}^{4}\)He, \(_{6}^{12}\)C, \(_{8}^{16}\)O
- Medium mass nuclides : (30 < A < 90) : In these nuclides, the binding energy per nucleon, \(\bar{B}\) increases from 8 MeV for A = 6 to 8.3 MeV for A having values 28 to 32 and further remains nearly constant 8.5 MeV. The nuclides falling on the maximum are most stable. 56Fe having \(\bar{B}\) values 8.79 MeV is extremely stable.
- Heavy nuclides (A > 90) : For heavy nuclides the \(\bar{B}\) values decrease from 8.79 to 7.7 MeV. 209Bi is the most stable nuclide. Beyond this all nuclides are unstable and radioactive.
Radioactivity :
Radioactivity : The phenomenon in which the unstable nuclei spontaneously undergo disintegration and emit a nuclear particle and gamma radiation transforming to a different nuclide is called radioactivity.
Radioactive elements : The elements which undergo spontaneous nuclear changes emitting nuclear particles are called radioactive elements.
- The radiations emitted by radioactive elements are : alpha (α), beta (β) and gamma (γ) radiations.
Radioactive decay :
Characteristics of radioactive decay :
- The probability of decay of a radioactive element does not depend on state of a chemical combination, temperature, pressure, presence of a catalyst and the age of radioactive nuclide.
- During radioactive decay, the radiations like alpha, beta and gamma are emitted.
- The radioactive decay continues until a stable isotope is formed.
- It is unidirectional irreversible process.
Rate of radioactive decay OR activity of radioelement : It denotes the number of nuclei of atoms of radioactive element which decay in unit time. It is also called activity of radioelement.
If dN is the number of nuclei that decay within time interval dt, then rate of decay at any time t is given by
rate of decay (activity) = \(-\frac{dN}{dt}\)
Rate law :
If dN is the number of nuclei that decay within time interval dt, then rate of decay at any time t is given by
Rate of decay (activity) = \(-\frac{dN}{dt}\)
This rate of decay is expressed as disintegrations per second and represented as dPs. Since the rate of decay is proportional to the number of nuclei (or atoms), it is represented as,
\(-\frac{dN}{dt}\) ∝ N Or \(-\frac{dN}{dt}\) = λ N …..(1)
where the constant λ is called decay constant or disintegration constant. It is characteristic of radioactive element.
Expression for decay constant :
Rearranging the Eq. (1)
\(-\frac{dN}{dt}\) = λ N
∴ \(-\frac{dN}{N}\) = λ dt
If N0 is the initial number of atoms i.e. at t = 0 and N the number of atoms present after time t then, by integration,
\(\int_{N_0}^{N} -\frac{dN}{N}\) = \(\int_{0}^{t}\)λ dt
∴ \(-\int_{N_0}^{N} \frac{dN}{N}\) = λ\(\int_{0}^{t}\) dt
∴ − ln\(\frac{N}{N_0}\) = λt
∴ ln\(\frac{N_0}{N}\) = λt
∴ λ = \(\frac{1}{t}\)ln\(\frac{N_0}{N}\) OR λ = \(\frac{2.303}{t}\)log10\(\frac{N_0}{N}\) ….(1)
This is an expression for decay constant.
Half life of a radioactive element : It is the time required for a given number of radioactive nuclei (or atoms) to decay exactly to half of its initial value.
Expression :
At t = 0, N = N0.
Hence at t = t1/2, N = N0/2
substitution of these values of N and t in Eq. λ = \(\frac{2.303}{t}\)log10\(\frac{N_0}{N}\)
∴ λ = \(\frac{2.303}{t_{1/2}}\)log10\(\frac{N_0}{N_0/2}\)
∴ λ = \(\frac{2.303}{t_{1/2}}\)log10 2 = \(\frac{2.303×0.3010}{t_{1/2}}\) = \(\frac{0.693}{t_{1/2}}\)
∴ t1/2 = \(\frac{0.693}{λ}\)
Graphical representation of decay :
λ = \(\frac{2.303}{t}\)log10\(\frac{N_0}{N}\)
∴ \(\frac{λt}{2.303}\) = log10 N0 — log10 N
∴ log10 N = \(-\frac{λt}{2.303}\) + log10 N0
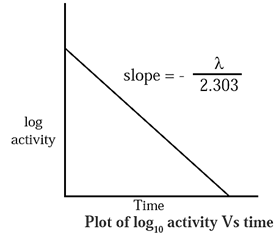
If a is activity of a radioelement then,
log10 a = \(-\frac{λt}{2.303}\) + log10 a0
where a0 is initial activity.
When log10 a is plotted versus t a straight line with negative slope is obtained,
∴ slope = \(-\frac{λt}{2.303}\)
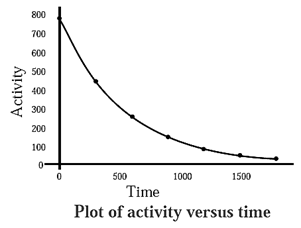
Variation in activity of a radioelement with time graph :
The rate of radioactive decay of a radioactive element at any instant is proportional to its number of atoms present at that instant.
The number of atoms of at radioelement decreases with time. Hence, the activity also decreases with time.
The number of atoms N0 at any instant is given by,
N = N0 e—λt
Hence, activity is represented as,
a = a0 e—λt
where a0 is initial activity and ’a’ is after time t.
This exponential decay is represented in the below diagram.
Units of radioactivity : Rate of radioactive decay is expressed in dps.
The unit for the radioactivity is curie (Ci).
1 Ci = 3.7 x 1010 dps (disintegrations per second)
Another unit of radioactivity is Becquerel (Bq)
1 Bq = 1 dps. Thus, 1Ci = 3.7 x 1010 dps = 3.7 x 1010 Bq
Modes of decay :
Radioelements decay by 3 ways, namely, α-decay, β- decay and γ- emission.
Alpha decay :
- The emission of α -particle from the radioactive nuclei is called α -decay.
- α -particle has +2 unit charge and 4 u mass.
- Hence on-particle is identified with helium nucleus and designated with \(_{2}^{4}\)He
- On emission of α -particle, the parent element loses 2 protons and 2 neutrons, thus losing 4 u mass.
- The daughter element thus formed has mass 4 units less and charge or atomic number less by 2 units than its parent element.
\(_{Z}^{A}\)X → \(_{Z-2}^{A-4}\)Y + \(_{2}^{4}\)He
Parent Daughter α-particle
\(_{88}^{226}\)Ra → \(_{88}^{226}\)Rn + \(_{2}^{4}\)He
Parent Daughter α-particle
- The daughter element formed occupies two places (groups) to the left of the parent element in the periodic table.
β -decay :
- β -particle is identified with negatively charged electron carrying — 1 charge and negligible mass and represented as β_ or \(_{-1}^{0}\)e
- The emission of high speed electron forming a new nuclide is called β -decay or β_ -decay.
- When a radioactive element loses a β -particle, then daughter element formed has same mass number but atomic number increases by 1 unit.
The daughter element occupies one place higher to the right of the parent element in the periodic table with one group higher.
\(_{Z}^{A}\)X → \(_{Z+1}^{A}\)Y + \(_{-1}^{0}\)e
Parent Daughter α-particle
\(_{93}^{238}\)Np → \(_{94}^{238}\)Pu + \(_{-1}^{0}\)e
Parent Group 6 Parent Group 7 .
γ - emission :
- γ - rays are high energetic electromagnetic waves not carrying any charge or mass.
- When a parent radioelement emits γ - ray the same element is formed as a daughter element with less energy.
\(_{90}^{234}\)Th → \(_{90}^{234}\) Th + γ
Higher energy Lower energy emmision
- γ -Radiation is almost always accompanied with α and β decay processes. In α and β decay process, the daughter nucleus formed is in energetically excited state.
\(_{92}^{232}\)U → \(_{90}^{234}\)Th (Radioactive ) + \(_{2}^{4}\)He
\(_{90}^{234}\)Th → \(_{90}^{234}\)Th + γ
High energetic Low energetic .
Nuclear reactions :
Transmutation : The nuclear transmutation is transformation of a stable nucleus into another nucleus be it stable or unstable.
Artificial radioactivity : The nuclear transmutation where the product nucleus is radioactive is called artificial radioactivity.
Comparison of chemical reactions and nuclear reactions :
| Chemical reactions | Nuclear reactions |
| It involves rearrangement of atoms by breaking and forming of chemical bonds. | In this reaction elements or isotopes of one elements are converted into another element in a nuclear reaction. |
| Different isotopes of an element have same behaviour. | Different isotopes of an element behave differently. |
| Only outer shell electrons take part in the chemical reaction. | In addition to electrons, protons, neutrons, other elementary particles may be involved. |
| Relatively small amount of energy is involved. | Nuclear reactions involve very large amount energy. |
| The rates of reactions are influenced by concentration, temperature, pressure and catalyst. | The rates of reaction are not influenced by temperature, pressure and catalyst. |
Induced or artificial radioactivity :
- It is a nuclear transmutation reaction in which the stable nucleus is converted into radioactive
- This radioactive nucleus decays spontaneously with emission of particles and radiation.
- This reaction is brought about by bombarding stable nuclei with high energetic
- projectiles like on-particles (\(_{2}^{4}\)He ).
\(_{5}^{10}\)Be + \(_{2}^{4}\)He → \(_{7}^{13}\)N (radioactive) + \(_{0}^{1}\)n
\(_{7}^{13}\)N → \(_{6}^{13}\)C + \(_{0}^{+1}\)e (positron)
Nuclear fission :
- This involves the splitting of a heavy nucleus of an atom into two nearly equal fragments along with the release of large amount of energy.
- Consider the nuclear fission of 235U isotope by neutron.
\(_{92}^{235}\)U + \(_{0}^{1}\)n → \(_{56}^{142}\)Ba + 36Kr + 3 \(_{0}^{1}\)n + energy
- Each fission may lead to different products. The mass of fission products is less than the mass of parent nucleus and energy equivalent to loss in mass or mass defect is emitted in the reaction.
- The reaction indicates that fission of one 235U nucleus emits 3 neutrons which further bring about the fission of three 235U nuclei and this process continues resulting a chain reaction releasing a large amount of energy in a short time.
- Fission of 235U takes place by 400 ways yielding 800 fission products many of which are radioactive producing new elements on disintegration.
- The energy released per fission is about 200 MeV. This self sustained chain reaction is highly explosive.
- This energy may be utilised for destructive purposes, defence purpose as well as for peaceful purposes (nuclear reactor-power plant), etc.
Nuclear fusion :
- A nuclear reaction in which small nuclei undergo combination or fusion forming nuclei of higher mass (at high temperature) is called nuclear fusion.
- During nuclear fusion enormous energy is released. High temperature is required for nuclear fusion reaction which is attained by carrying out nuclear reaction prior to it. These reactions occur in the Sun and stars continuously.
\(_{1}^{1}\)H + \(_{1}^{1}\)H → \(_{1}^{2}\)H + \(_{+1}^{0}\)e
\(_{1}^{1}\)H + \(_{1}^{2}\)H → \(_{2}^{3}\)He
\(_{2}^{3}\)He + \(_{2}^{3}\)He → \(_{2}^{4}\)He + 2\(_{1}^{1}\)H
\(_{2}^{3}\)He + \(_{1}^{1}\)H → \(_{2}^{4}\)He + \(_{+1}^{0}\)e
- Although nuclear fusion produces more energy per given mass of fuel, it is very difficult to carry out since it requires extremely high temperature, more than 108K which is achieved by nuclear fission. Hence, nuclear fusion cannot be used to produce energy.
Applications of Radio isotopes :
Radiocarbon dating : The technique is used to find the age of historic and archaelogical organic samples such as old wood samples and animal or human fossils.
(i) Radioactive 14C is formed in the upper atmosphere by bombardment of neutrons from cosmic rays on 14N.
\(_{7}^{14}\)N + \(_{1}^{0}\)n → \(_{6}^{14}\)C + \(_{1}^{1}\)H
(ii) 14C combines with atmospheric oxygen to form 14CO2 which mixes with ordinary 12CO2.
(iii) Carbon di oxide is absorbed by plants during photosynthesis. Animals eat plants. Hence, 14C becomes a part of plant and animal bodies.
(iv) As long as plant is alive, the ratio 14C/12C remains constant. When the plant dies, photosynthesis occurs no more and the ratio 14C/12C decreases with the decay of 14C (half life 5730 years).
\(_{6}^{14}\)C → \(_{7}^{14}\)N + \(_{-1}^{0}\)e
(v) The activity (N) of given wood sample and that of fresh sample of live plant (N0) is measured. N0 denotes, the activity of the given sample at the time of death.
(vi) The age of the given wood sample, rather the period over which it has remained dead can be determined.
t = \(\frac{2.303}{λ}\)log10\(\frac{N_0}{N}\)
where λ = \(\frac{0.693}{5730}\)y-1 = 1.21 x 104 y—1.
Electrical energy from Nuclear fission :
Nuclear power :
- It is the electricity made from nuclear fission of uranium and platinum.
- It releases zero carbon dioxide.
- It releases zero oxides of sulphur and nitrogen.
- It avoids atmospheric pollutants giving a clean energy.
- Thus it offers huge environmental benefits in producing electricity.
- Fission of 1 g of 235U produces about 24,000 kW/h of energy which is obtained by burning 3 tons of coal.
- Since traditional sources of fuel like oil, gas, coal are depleting, cost of petroleum is increasing, we have to shift to new energy source obtainable from nuclear fission.
Nuclear reactor :
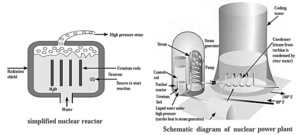
- A nuclear reactor is a device that uses atomic energy in a regulated way for peaceful purposes.
- In a nuclear reactor, fissionable material 235U 239Pu is stacked with moderator like heavy water (Deuterium oxide, D2O) or graphite.
- The moderator is used to obtain the slow neutrons needed to start the fission process.
- Cadmium rods are introduced into the moderator to absorb neutrons and regulate the chain reaction.
- The energy is released as heat, which is dissipated by circulating liquid coolant, which produces steam. The steam is then sent via turbines, which generate energy.
- As a result, atomic energy may be regulated and employed for peaceful reasons such as getting electrical energy, generating electricity for civilian uses, ships, submarines, and so on.
Applications of radioisotopes
In agriculture :
- Radioisotopes find wide applications in agriculture.
- The agricultural products are preserved by irradiating with gamma rays obtained from Co—60 or Cs-137.
- A genetic change in the growth of plants is brought about by irradiating with gamma rays, BARC had displayed it in gamma garden.
In medicine :
- Several radioisotopes are used for diagnostic purposes and for the treatment of several diseases.
- The short-lived isotopes are used for diagnostic purposes to limit the exposure time to radiations.
- Therapeutic radioisotopes are used to destroy abnormal cells like cancerous
Therapeutic Radioisotopes :

Diagnostic Radioisotopes :

In radio-tracer technique :
- In this technique one or more atoms of a chemical compound are replaced by a radionuclide to trace the path followed by that chemical in the system under study by radioactivity measurement.
Class-11-Chemistry-Chapter-13-Nuclear Chemistry and Radioactivity-Text Book
Class-11-Chemistry-Chapter-13-Nuclear Chemistry and Radioactivity- Notes
Class-11-Chemistry-Chapter-13-Nuclear Chemistry and Radioactivity-Solution
Main Page : – Maharashtra Board Class 11th-Chemistry – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter-12-Chemical Equilibrium – Online Notes
Next Chapter : Chapter-14-Basic Principles of Organic Chemistry – Online Notes