Notes-Part-2
Ideal Gas Equation :
Ideal gas :
- A gas that follows strictly all the three laws; Boyle's law, Charles' law and Avogadro law and ideal gas equation (PV = nRT) is an ideal gas.
- Molecules are perfectly elastic.
- No attraction or repulsion between the gas molecules i.e. collision without loss of kinetic energy (K.E.)
- Actual volume of the gas molecules is negligible as compared to total volume of the gas.
- It doesn't liquify even at low temperature but continues to obey Charles’ law and finally occupies zero volume at — 273 °C.
- Such a gas does not exist.
Real gas :
- A gas which does not obey gas laws or an ideal gas equation is called a real gas.
- Practically almost all gases are real gases but they tend towards an ideal behaviour at low pressure and high temperature.
- Molecules are not perfectly elastic.
- Intermoleculer attraction is present, hence, collision takes place with loss of kinetic energy.
- Actual volume of individual gas molecule is significant at high pressure and low temperature.
- Undergoes liquefaction at low temperature when cooled and compressed.
- Gases that exist in nature like H2, O2, CO2, N2, He, etc.
Derivation of Ideal Gas Equation :
The three gas laws, namely, Boyle’s law, Charles law and Avogadro law, are combined mathematically to obtained what is called ideal gas equation.
Consider n moles of a gas occupying volume V at pressure P and temperature T.
(i) By Boyle's law, at constant temperature,
V ∝ 1/P (at constant n and T)
(ii) By Charles’ law, at constant pressure,
V ∝ T (at constant n and P)
(iii) By Avogadrds law, at constant pressure and temperature,
V ∝ n (at constant P and T)
Hence,
V ∝ \(\frac{n×T}{P}\)
∴ V = \(\frac{nRT}{P}\) OR PV = nRT
where R is a proportionality constant and called gas constant or universal gas constant.
The equation, PV = nRT is called an ideal gas equation or an equation of state.
- If m is the mass of the gas then, number of moles, n = m/M Hence, ideal gas equation can be written as, PV = \(\frac{mRT}{M}\).
Values of ‘R’ in different Units :
The value of R depends upon the units used to express P, V and T. Hence we recall
STP conditions for determining values of ‘R’.
(i) R in SI Unit (in Joules) : Value of R can be calculated by using the SI units of P,V and T. Pressure P is measured in N m-2 or Pa, volume V in meter cube (m3) and Temperature T in kelvin (K),
R = \(\frac{PV}{nT}\)
∴ R = \(\frac{10^5Pa×22.71×10^{-3}m^3}{1\,mole×273.15\,K}\)
∴ R = 8.314 Pa m3 K-1 mol-1
then R = 8.314 JK-1 mol-1
(ii) R in litre atmosphere : If pressure (P) is expressed in atmosphere (atm) and volume in litre (L) or decimeter cube (dm3) and Temperature in kelvin (K), (that is, old STP conditions), then value of R is :
R = \(\frac{1\,atm×22.414\,L}{1\,mole×273.15\,K}\)
∴ R = 0.08206 L atm K-1 mol -1
OR
R = 0.08206 dm3 atm K-1mol-1
(iii) R in calories:
1 calorie = 4.184 Joules
∴ R = \(\frac{8.314}{4.184}\) = 1.987 cal K-1 mol-1
Note : While using ideal gas equation one should use consistent units.
- Often Pressure (P) is measured in atmosphere (atm). The conversion between the units is done by noting that 1 atm = 1.013 × 105 Nm-2 or 1 atm = 101.3 kPa
Table-Unit of R :
| Pressure (P) | Volume (V) | Number of moles (n) | Temperature (T) | Gas constant
(R) |
| Pa (pascals) | m3 | mol | K | 8.314 J K-1 mol-1 |
| atm | dm3 | mol | K | 0.0821 atm dm3 K-1 mol-1 |
| atm | L | mol | K | 0.0821 L atm K-1 mol-1 |
Relation between density, molar mass and pressure of the gas :
For 'n’ moles of an ideal gas at pressure P, temperature T occupying volume V, by ideal gas equation,
PV = nRT
If m is the mass and M molar mass of the gas then,
n = \(\frac{\text{mass of a gas}}{\text{molar mass of a gas}}=\frac{m}{M}\)
∴ PV = \(\frac{m}{M}\)RT
∴ \(\frac{PM}{RT}=\frac{m}{V}\) ….(1)
The density of the gas is,
d = \(\frac{m}{V}\) ∴ d = \(\frac{PM}{RT}\)
Hence, Boyle's law in terms of density may be stated as, pressure of a gas at constant temperature is directly proportional to its density.
Expression for Molar mass :
From above, equation (1) \(\frac{PM}{RT}=\frac{m}{V}\)
∴ M = \(\frac{mRT}{PV}\)
Combined Gas law :
Consider n moles of a gas. By ideal gas equation,
PV = nRT
∴ \(\frac{PV}{T}\) = nR = constant. (Since n and R are constant)
Hence, for a given gas,
\(\frac{P_1V_1}{T_1}=\frac{P_2V_2}{T_2}\)
This equation is also called Combined gas law or combined gas equation.
Dalton’s law of Partial Pressure :
Partial pressure : The pressure exerted by an individual gas in a gaseous mixture of two or more gases is called partial pressure of the gas.
Mathematical expression for Dalton’s law of partial pressure :
Statement : The total pressure of a mixture of two or more unreactive gases is the sum of the partial pressures of the individual gases in the mixture.
If P1, P2, P3, .... .. are partial pressures of constituent gases in the mixture at constant volume and temperature then by Dalton’s law, total pressure is,
PTotal = P1 + P2 + P3 + .... ..
This is mathematical statement of Dalton’s law.
Relation between partial pressure and mole fraction of a gas :
Consider a gaseous mixture containing n1, n2, n3, .... .. moles of gaseous constituents in a container of volume V at pressure P and temperature T.
Then their partial pressures will be,
P1 = \(\frac{n_1RT}{V}\), P2 = \(\frac{n_2RT}{V}\), P3 = \(\frac{n_3RT}{V}\) …..
By Dalton's law, the total pressure of gaseous mixture is,
PTotal = P1 + P2 + P3 + .... ..
= \(n_1(\frac{RT}{V})+n_2(\frac{RT}{V})+n_3(\frac{RT}{V})\)…..
= (n1 + n2 + n3 + …..)\(\frac{RT}{V}\)
∴ PTotal = \(\frac{nRT}{V}\)
where n is total number of moles of all gaseous components.
The mole fraction of each constituent gas is given by,
X1 = \(\frac{n_1}{n}\), X2 = \(\frac{n_2}{n}\), X3 = \(\frac{n_3}{n}\), ……
∴ X1 = \(\frac{n_1}{n}=\frac{P_1/(RT/V)}{P_{Total}/(RT/V)}=\frac{P_1}{P_{Total}}\)
P1 = X1 × PTotal
Hence in general for ith constituent,
Pi = Xi × PTotal
This is a relation between partial pressure and mole fraction of a gas.
Thus partial pressure of a gas is obtained by multiplying the total pressure of mixture by mole fraction of that gas.
| Know This :
Application of Dalton law : Of course, the most significant gas combination is the air we breathe. Dalton's law is useful for studying many air phenomena, such as air pollution. Each constituent's composition in air may be estimated. |
Aqueous tension : In case of pure water or an aqueous solution, there exists saturated water vapour in equilibrium with it on its surface and the pressure of this vapour is called aqueous tension.
Pressure of pure and dry gas can be calculated by using the aqueous tension. It is
obtained by subtracting the aqueous tension from total pressure of moist gas.
∴ PDry gas = PTotal - Paq
i.e. PDry gas = PTotal - Aqueous Tension
Aqueous Tension of Water (Vapour Pressure) as a function of Temperature :
| Temp. (K) | Pressure (bar) | Temp. (K) | Pressure (bar) |
| 273.15 | 0.0060 | 295.15 | 0.0260 |
| 283.15 | 0.0121 | 297.15 | 0.0295 |
| 288.15 | 0.0168 | 299.15 | 0.0331 |
| 291.15 | 0.0204 | 301.15 | 0.0372 |
| 293.15 | 0.0230 | 303.15 | 0.0418 |
The above table reflects that Aqueous Tension increases with increase in temperature.
Kinetic Molecular Theory of Gases :
The kinetic molecular theory of gases is a theoretical model put forth to explain the behavior of gases.
Postulates of kinetic molecular theory of gases :
- Gases consist of tiny particles (molecules or atoms).
- On an average, gas molecules remain far apart from each other. Therefore the actual volume of the gas particles is negligible as compared to the volume of the container. (That is why the gases are highly compressible).
- The attractive forces between the gas molecules are negligible at ordinary temperature and pressure. (As a result gas expands to occupy entire volume of the container).
- Gas molecules are in constant random motion and move in all possible directions in straight lines. They collide with each other and with the walls of the container.
- Pressure of the gas is due to the collision of gas particles with the walls of container.
- The collisions of the gas molecules are perfectly elastic in nature, which means
- that the total energy of the gaseous particle remains unchanged after collision.
- The different molecules of a gas move with different velocities at any instant and hence have different kinetic energies. But average kinetic energy of the gas molecules is directly proportional to the absolute temperature. Average K.E. ∝ T
Kinetic gas equation :
A mathematical gas equation derived from the basic postulates of the kinetic energy of gases and from which all the gas laws can be deduced is called a kinetic gas equation.
It is represented as,
PV = \(\frac{1}{3}mnu^2\)
where,
P = pressure, exerted by the gas molecules
V = volume of a container,
n = number of molecules of the gas
m = mass of a gas molecule
u = velocity of gas molecules
Deviation from Ideal behaviour :
An ideal gas is the one that exactly follows the ideal gas equation. Real gas does not obey Boyle’s law and Charles' law under all the conditions of temperature and pressure.
A deviation from the ideal behavior is observed a high pressure and low
Temperature. It is due to two reasons.
- The intermolecular attractive forces are not negligible in real gases. These do not allow the molecules to collide the container wall with full impact. This results in decrease in the pressure.
- At high pressure, the molecular are very close to each other. The short range repulsive forces start operating and the molecules behave as small but hard spherical particles.
The volume of the molecule is not negligible. Therefore, x less volume is available for molecular motion.
At very low temperature, the molecular motion becomes slow and the molecules are attracted to each other due to the attractive force. Hence, here again the behaviour of the real gas deviates from the ideal gas behaviour.
Deviation with respect to pressure can be studied by plotting pressure (P) vs volume (V) curve at a given temperature. (Fig.)
Deviation from ideal behaviour can be measured in terms of compressibility factor Z
Compressibility Factor (Z) :
Compressibility factor: It is defined as the ratio of product of pressure and volume (PV) for a gas to nRT and mathematically represented as
Z = \(\frac{PV}{nRT}\)
where,
n = number of moles of a gas
T = absolute temperature
R = gas constant.
Consider n moles of a gas at pressure P and temperature T. If it behaves ideally, then the volume of the gas will be as obtained from the
ideal gas equation, P × Videal = nRT
Hence, the compressibility factor will be,
Z = \(\frac{PV_{ideal}}{nRT}\)
For ideal gas, Z = 1, hence PVideal = nRT
If the gas deviates from the ideal behaviour, then it will be a non-ideal gas or a real gas.
Then
Z = \(\frac{PV_{real}}{nRT}\)
∴ PVreal = ZnRT
∴ \(\frac{PV_{real}}{PV_{ideal}}=\frac{ZnRT}{nRT}\) = Z
∴ Z = \(\frac{V_{real}}{V_{ideal}}\)
Hence, compressibility factor can be defined as the ratio of actual volume of a gas due to non-ideal behaviour to the volume of the same gas due to ideal behaviour at the same temperature and pressure.
Variation in the compressibility factor (Z) with pressure for dinitrogen gas at different constant temperatures :
The compressibility factor Z for a gas at a pressure P and temperature T is defined as, Z = \(\frac{PV}{nRT}\)
For an ideal gas, Z = 1, hence PV= nRT.
For a non-ideal or real gas, z ≠ 1, hence, PV ≠ nRT. For a gas, the deviation in the value of Z from unit value is a measure of its deviation from ideal behaviour.
The variation in Z value for nitrogen gas with pressure is shown in different isotherms in below Fig. at different constant temperatures.
Explanation :
- For an ideal gas the compressibility factor Z is independent of pressure and temperature. For a non-ideal or real gas, Z changes with pressure and temperature.
- At very low pressure (P ≅ 0), the gas tends to behave ideally and all isotherms start at Z = 1.
- At low temperatures the intermolecular attractive forces become prominent.
Liquefaction of gases and critical constant :
Most gases behave like ideal gases at high temperature. Liquefaction phenomenon of gases can be studied by plotting the graphs of pressure versus volume at various constant temperatures.
- Consider the liquefaction of CO2 At 50 °C, the gas behaves ideally and throughout the pressure change it remains in the gaseous state.
- At low temperature, 13.10 °C as the pressure is increased from A, CO2 starts liquefying at B, and the liquefaction becomes complete at C.
- Further increase in pressure decreases the volume of liquid CO2 along CD but to a very less extent compared to gaseous state. Along BC region liquid and gas coexist in equilibrium.
- When the liquefaction of CO2 is studied at higher temperatures, the region BC decreases.
- At 30.98 °C the region BC reduces to a point Q, which is called critical point. Above this point and temperature, CO2 doesn't exist in the liquid state, however pressure may be applied.
Critical constant :
- Critical temperature (TC) : The temperature of a critical point and above which a gas cannot exist in the liquid state is called critical temperature.
- Critical volume (VC) : The molar volume at critical temperature and the critical point is called critical volume.
- Critical pressure (PC) : The pressure of a gas at critical temperature and critical volume is called critical pressure.
Easily liquefiable gases have higher critical temperatures.
Critical constants for common Gases :
| Substance | Tc / K | Pc/ bar | Vc/dm3mol-1 |
| He | 5.3 | 2.29 | 0.0577 |
| H2 | 33.2 | 12.97 | 0.0650 |
| N2 | 126.0 | 33.9 | 0.0900 |
| O2 | 154.3 | 50.4 | 0.0744 |
| CO2 | 304.10 | 73.9 | 0.0956 |
| NH3 | 405.5 | 113.0 | 0.0723 |
| H2O | 647.1 | 220.6 | 0.0450 |
Fluid : Fluid is any substance either liquid or gas, in which the molecules are relatively mobile and can flow.
Remember :
|
Liquid state :
Properties of a liquid :
- Liquid state is the intermediate state between gaseous state and solid state.
- Molecules of a liquid are held together by moderately strong intermolecular forces.
- A liquid has fluidity, takes the shape of vessel of the container.
- Every liquid has definite boiling point, freezing point, viscosity and surface tension.
Vapour Pressure :
The pressure exerted by the vapour in equilibrium with the liquid is known as saturated vapour pressure or simply vapour pressure.
The vapour pressure of water is also called Aqueous Tension.
Explanation :
- All liquids have a tendency of evaporation, during which liquid molecules escape into a gaseous state (vapour).
- If the vessel is closed then the vapour molecules get accumulated on the liquid surface.
- These molecules due to random motion collide with each other and on the walls of a container and get condensed back into the liquid.
- When an equilibrium is attained between evaporation and condensation the number of vapour molecules remain constant giving a definite vapour pressure at constant temperature.
- Mercury manometer may be used to measure the vapour pressure of a‘ liquid as shown in below Fig.
Factors affecting vapour pressure of a liquid :
- Nature of liquid : The liquids having relatively weak intermolecular forces possess high vapour pressure. These are called valatile liquids. For example, petrol evaporates quickly than motor oil. The liquids having low vapour pressure are called non-volatile liquids.
- Temperature : As the temperature increases, the vapour pressure of the liquid increases.
Unit of vapour pressure :
- Vapour pressure is measured by means of a manometer.
- The most common unit for vapour pressure is torr. 1 torr = 1 mm Hg.
Surface Tension :
The force acting per unit length perpendicular to the line drawn on the surface of liquid is called surface tension.
- Unit : Surface tension is measured in SI Unit, Nm-1, denoted by Greek letter “γ’’ (Gamma)
Explanation:
- In the bulk of a liquid, every molecule is surrounded equally and symmetrically by other neighbouring molecules of the liquid. Hence, all bulk molecules experience balanced forces.
- But on the surface, the molecules experience downward attractive forces from the molecules in the bulk.
- Since there are no molecules above the liquid surface they experience net force of attraction in the downward direction towards the bulk of the liquid. Therefore, the liquid surface behaves like a ‘stretched membrane which is always under a tension. This gives rise to a surface tension on the liquid surface.
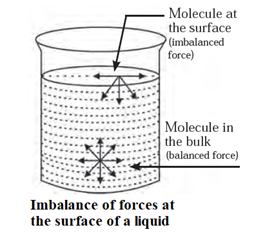
Factors affecting on Surface tension :
- Surface tension is a temperature dependent property.
- When attractive forces are large, surface tension is large.
- Surface tension decreases as the temperature increases.
- With increase in temperature, kinetic energy of molecules increases. So intermolecular forces of attraction decrease, and thereby surface tension decreases.
Application of surface tension :
- Cleaning action of soap and detergent is due to the lowering of interfacial tension between water and oily substances. Due to lower surface tension, the soap solution penetrates into the fibre, surrounds the oily substance and washes it away.
- The effective use of toothpastes, mouth washes and nasal drops is due to the presence of substances having lower surface tension. This increases the efficiency of their penetrating action.
Viscosity :
Viscosity is the force of friction between the successive layers of a flowing liquid.
OR
It is the resistance to the flow of a liquid.
Explanation :
- When a liquid flows, it is considered to be moving in different layers in contact with one another.
- There is a force of friction between the adjacent layers of a moving liquid which opposes the motion of the liquid.
- When a liquid flows over a fixed surface, the layer of the molecules in the immediate contact of the surface experiences maximum friction and it is considered stationary.
- As the distance of upper layers increases from the fixed layer the velocity increases. Hence, there is a regular gradation of velocity of moving liquid layers from one layer to the next, and this flow is called laminar flow.
Factors affecting on Viscosity :
- Viscosity is a temperature dependent property.
Viscosity ∝ \(\frac{1}{Temperature}\)
- Viscosity depends on molecular size and shape. Larger molecules have more
- viscosity and spherical molecules offer the least resistance to flow and therefore are less viscous.
- Greater the viscosity, slower is the liquid flow.
Unit : Viscosity is expressed in terms of coefficient of viscosity, ‘η’ (Eta). It is defined as the degree to which a fluid resists flow under an applied force, measured by the tangential frictional force per unit area per unit velocity gradient when the flow is laminar.
- SI unit of viscosity coefficient is N s m-2 (newton second per square meter).
- In CGS (η) is measured in poise. 1 poise = 1 gm cm-1s-1 = 10-1 kg m-1s-1
Illustration of viscosity :
- Lubricating oils are viscous liquids. Gradation of lubricating oils is done on the basis of viscosity. A good quality Lubricating oil does not change its viscosity with increase or decrease in temeperature.
- Increase blood viscosity than the normal value is taken as an indication of cardio vascular disease.
- Glass panes of old buildings are found to become thicker with time near the bottom. This is one evidence which indicates that glass is not a solid but a supercooled viscous liquid.