Basic Concepts in Geometry
Class-9-Mathematics-2-Chapter-1-Maharashtra Board
Notes
|
Topics to be learn :
|
Point, line and plane :
- We do not define a point, line and plane also. These are some basic concepts in Geometry.
- Lines and planes are sets of points.
Co-ordinates of a points and distance :
The number associated with a point on the number line is called its coordinate.
Example : In the below figure, the coordinate of point A is -5 and the coordinate of point D is 1.

Remember :
- The distance between the two points is obtained by subtracting the smaller coordinate from the larger coordinate.
- The distance between two distinct points is a nonnegative real number.
- If the two points are not distinct then the distance between them is zero.
Betweenness :
If P, Q, R are three distinct collinear points, there are three possibilities.
(i) Point Q is between P and R. ( Symbolically : P—Q—R )

(ii) Point R is between P and Q. ( Symbolically : P—R—Q )
![]()
(iii) Point P is between R and Q. ( Symbolically : R—P—Q )
![]()
If d (R,P) + d (P, Q) = d (R, Q), then it is said that point P is between points R and Q. This is shown as R—P—Q or Q—P—R
Line segment :
- The union set of point A, point B and points between A and B is called segment AB or seg AB. Seg AB means seg BA.
![]()
- Point A and point B are called the end points of seg AB.
- The distance between the end points of a segment is called the length of the segment. That is l(AB) = d (A,B)
- l(AB) = 10 is also written as AB = 10.
Ray AB :
- If A and B are two distinct points. The union set of all points on seg AB and the points P such that A - B - P, is called ray AB. Here point A is called the starting point of ray AB.
- The union set of points on ray AB and opposite ray of ray AB is called line AB.
- The set of points of seg AB is a subset of points of line AB.
Congruent Segments :
- If the lengths of two segments are equal, then the two segments are congruent.

- In the above figure, AB = CD
- ∴ seg AB ≅ seg CD
Properties of congruent segements :
- Reflexivity : seg AB ≅ seg AB
- Symmetry : If seg AB ≅ seg CD then seg CD ≅ seg AB
- Transitivity : If seg AB ≅ seg CD and seg CD ≅ seg EF then seg AB ≅ seg EF
Midpoint of a segment :
- If A-M-B and seg AM ≅ seg MB, then M is called the midpoint of seg AB.
![]()
- Every segment has one and only one midpoint.
- In the figure, AM = MB = \(\frac{1}{2}\)AB
Comparison of segments :
- If l (AB) < l (CD), then seg AB < seg CD or seg CD > seg AB.
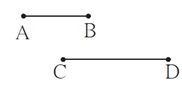
- The comparison of segments depends upon their lengths.
Perpendicularity of segments or rays :
- If the lines containing two segments, two rays or a ray and a segment are perpendicular to each other, then the two segments, two rays or the ray and the segment are said to be perpendicular to each other.
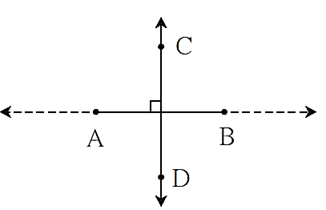
- In the figure, seg AB ⊥ line CD and seg AB ⊥ ray CD.
Distance of a point from a line :
- If seg CD ⊥ line AB and the point D lies on line AB then the length of seg CD is called the distance of point C from line AB.
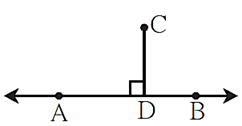
- The point D is called the foot of the perpendicular.
- If l(CD) = a, then the point C is at a distance of ‘a’ from the line AB.
Conditional statements and converse :
(i) The statements which can be written in the ‘If — then’ form are called conditional statements.
Example :
Statement : The diagonals of a rhombus are perpendicular bisectors of each other.
Conditional statement : ‘If the given quadrilateral is a rhombus then its diagonals are perpendicular bisectors of each other.’
- The part of the statement following ‘If” is called the antecedent.
- The part of the statement following ‘then’ is called the consequent.
(ii) If the antecedent and consequent in a given conditional statement are interchanged, the resulting statement is called the converse of the given statement.
(iii) If a conditional statement is true, its converse is not necessarily true.
Example :
(a) Conditional statement : If a quadrilateral is a rhombus then its diagonals are perpendicular bisectors of each other.
Converse : If the diagonals of a quadrilateral are perpendicular bisectors of each other then it is a rhombus.
- In the above example, the statement and its converse are true.
(b) Conditional statement : If a number is a prime number then it is even or odd.
Converse : If a number is even or odd then it is a prime number.
- In this example, the statement is true, but its converse is false.
Proof :
- Some self evident geometrical statements are called postulates.
- The properties which are proved logically are called theorems.
- The logical argument put forward to prove a theorem is called its proof.
- When we are going to prove that a conditional statement is true, its antecedent is called ‘Given part’ and the consequent is called ‘the part to be proved.”
- There are two types of proofs, Direct and Indirect.
Some of Euclid’s postulates are given below :
(1) There are infinite number of lines passing through a point.
(2) There is one and only one line passing through two points.
(3) Acircle of given radius can be drawn taking any point as its centre.
(4) All right angles are congruent with each other.
(5) If two interior angles formed on one side of a transversal of two lines add up to less than two right angles, then the lines produced in that direction intersect each other.

∠ a + ∠ b ≠ 180°
∴ line l intersects line m.
Direct and Indirect proofs :
Examples :
(i) Direct proof of the property of angles made by two intersecting lines.
Theorem : The opposite angles formed by two intersecting lines are of equal measures.
Given : Line AB and line CD intersect each other at the point O such that O—A—B, C—O—D.
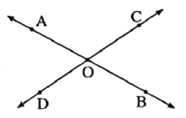
To prove :
(i) ∠ AOC = ∠ BOD
(ii) ∠ BOC = ∠ AOD
Proof :
∠ AOC + ∠ AOD = 180° ... (Angles in a linear pair) ... (1)
∠ AOD + ∠ BOD = 180° ...(Angles in a linear pair) ... (2)
∴ ∠ LAOC + ∠ AOD = ∠ AOD + ∠ BOD ... [From (1) and (2)]
∴ ∠ AOC = ∠ BOD ... (Eliminating ∠ AOD)
Similarly, We can prove, ∠ BOC = ∠ AOD.
(ii) Indirect proof :
This type of proof starts with an assumption that the consequence is false.
Statement : A prime number greater than 2 is odd.
Conditional statement : If p is a prime number greater than 2 then it is odd.
Given : p is a prime number greater than 2. That is, 1 and p are the only divisors of p.
To prove : p is an odd number.
Proof : Let us suppose that p is not an odd number.
So p is an even number
∴ a divisor of p is 2 ..... (1)
But it is given that p is a prime number greater than 2 ....(given)
∴ 1 and p are the only divisors of p ..... (2)
Statements (1) and (2 ) are contradictory.
∴ the assumption , that p is not odd is false.
This proves that a prime number greater than 2 is odd.
PDF-Notes,Solution,Text Book
Main Page : – Maharashtra Board Class 9th-Mathematics – All chapters notes, solutions, videos, test, pdf.
Next Chapter : Chapter-2-Parallel Lines – Online Notes