Basic Concepts in Geometry
Class-9-Mathematics-2-Chapter-1-Maharashtra Board
Notes
Practice set 1.1 :
Question 1. Find the distances with the help of the number line given below :

(i) d(B, E)
The distance between the two points is obtained by subtracting the smaller coordinate from the larger coordinate.
To find d(B, E) :
2 is a coordinate of point B
5 is a coordinate of point E.
5 > 2
∴ d(B, E) = 5 – 2 = 3
Answer is : d(B, E) = 3.
(ii) d(J, A)
The distance between the two points is obtained by subtracting the smaller coordinate from the larger coordinate.
To find d(J, A) :
—2 is a coordinate of point J
1 is a coordinate of point A.
1 > —2
∴ d(J, A) = 1 – (—2) = 1 + 2 = 3
Answer is : d(J, A) = 3.
(iii) d(P, C)
The distance between the two points is obtained by subtracting the smaller coordinate from the larger coordinate.
To find d(P, C) :
—4 is a coordinate of point P
3 is a coordinate of point C.
3 > —4
∴ d(P, C) = 3 – (—4) = 3 + 4 = 7
Answer is : d(P, C) = 7.
(iv) d(J, H)
The distance between the two points is obtained by subtracting the smaller coordinate from the larger coordinate.
To find d(J, H) :
—2 is a coordinate of point J
—1 is a coordinate of point H.
—1 > —2
∴ d(J, H) = —1 – (—2) = —3 + 2 = 1
Answer is : d(J, H) = 1.
(v) d(K, O)
The distance between the two points is obtained by subtracting the smaller coordinate from the larger coordinate.
To find d(K, O) :
—3 is a coordinate of point K
0 is a coordinate of point O.
0 > —3
∴ d(K, O) = 0 – (—3) = 0 + 3 = 3
Answer is : d(K, O) = 3.
(vi) d(O, E)
The distance between the two points is obtained by subtracting the smaller coordinate from the larger coordinate.
To find d(O, E) :
0 is a coordinate of point O
5 is a coordinate of point E.
5 > 0
∴ d(O, E) = 5 – 0 = 5
Answer is : d(O, E) = 5.
(vii) d(P, J)
The distance between the two points is obtained by subtracting the smaller coordinate from the larger coordinate.
To find d(P, J)
—4 is a coordinate of point P
—2 is a coordinate of point J.
—2 > —4
∴ d(P, J) = —2 – (—4) = —2 + 4 = 2
Answer is : d(P, J) = 2.
(viii) d(Q, B)
The distance between the two points is obtained by subtracting the smaller coordinate from the larger coordinate.
To find d(Q, B)
—5 is a coordinate of point Q
2 is a coordinate of point B.
2 > —5
∴ d(Q, B) = 2 – (—5) = 2 + 5 = 7
Answer is : d(Q, B) = 7.
Question 2. If the co—ordinate of A is x and that of B is y, find d(A, B) .
(i) x = 1, y = 7
Coordinate of point A is x = 1.
Coordinate of point Bis y = 7
7 > 1
∴ d(AB) = 7 – 1 = 6Answer is : d(AB) = 6
(ii) x = 6, y = — 2
Coordinate of point A is x = 6.
Coordinate of point B is y = —2
6 > —2
∴ d(AB) = 6 – (—2) = 6 + 2 = 8Answer is : d(AB) = 8
(iii) x = — 3, y = 7
Coordinate of point A is x = —3
Coordinate of point B is y = 7
7 > —3
∴ d(AB) = 7 – (—3) = 7 + 3 = 10Answer is : d(AB) = 10
(iv) x = — 4, y = — 5
Coordinate of point A is x = —4
Coordinate of point B is y = —5
—4 > —5
∴ d(AB) = —4 – (—5) = —4 + 5 = 1Answer is : d(AB) = 1
(v) x = — 3, y = — 6
Coordinate of point A is x = —3
Coordinate of point B is y = —6
—3 > —6
∴ d(AB) = —3 – (—6) = —3 + 6 = 3Answer is : d(AB) = 3
(vi) x = 4, y = — 8
Coordinate of point A is x = 4
Coordinate of point B is y = —8
4 > —8
∴ d(AB) = 4 – (—8) = 4 + 8 = 12Answer is : d(AB) = 12
Question 3. From the information given below, find which of the point is between the other two. If the points are not collinear, state so.
(i) d(P, R) = 7, d(P, Q) = 10, d(Q, R) = 3
d(P, R) = 7, d(P, Q) = 10, d(Q, R) = 3 ….(given)
d(P, R) + d(Q, R) = 7 + 3 = 10
d(P, Q) = 10
∴ d(P, R) + d(Q, R) = d(P, Q)
∴ points P, Q and R are collinear.
Point R lies between points P and Q.
Answer is : P—R—Q or Q—R—P.
(ii) d(R, S) = 8, d(S, T) = 6, d(R, T) = 4
d(R, S) = 8, d(S, T) = 6, d(R, T) = 4 ….(given)
d(S, T) + d(R, T) = 6 + 4 = 8
d(R, S) = 8
∴ d(S, T) + d(R, T) ≠ d(R, S)
∴ points R, S and T are not collinear.
Answer is : Points R, S and T are not collinear.
(iii) d(A, B) = 16, d(C, A) = 9, d(B, C) = 7
d(A, B) = 16, d(C, A) = 9, d(B, C) = 7 ….(given)
d(C, A) + d(B, C) = 9 + 7 = 16
d(A, B) = 16
∴ d(C, A) + d(B, C) = d(A, B)
∴ points A, B and C are collinear.
Point C lies between points A and B.
Answer is : A—C—B or B—C—A.
(iv) d(L, M) = 11, d(M, N) = 12, d(N, L) = 8
d(L, M) = 11, d(M, N) = 12, d(N, L) = 8 ….(given)
d(L, M) + d(N, L) = 11 + 8 = 19
d(M, N) = 12
∴ d(L, M) + d(N, L) ≠ d(M, N)
∴ points L, M and N are not collinear.
Answer is : Points L, M and N are not collinear.
(v) d(X, Y) = 15, d(Y, Z) = 7, d(X, Z) = 8
d(A, B) = 16, d(C, A) = 9, d(B, C) = 7 ….(given)
d(C, A) + d(B, C) = 9 + 7 = 16
d(A, B) = 16
∴ d(C, A) + d(B, C) = d(A, B)
∴ points A, B and C are collinear.
Point C lies between points A and B.
Answer is : A—C—B or B—C—A.
(vi) d(D, E) = 5, d(E, F) = 8, d(D, F) = 6
d(D, E) = 5, d(E, F) = 8, d(D, F) = 6 ….(given)
d(D, E) + d(D, F) = 5 + 6 = 11
d(E, F) = 8
∴ d(D, E) + d(D, F) ≠ d(E, F)
∴ points D, E and F are not collinear.
Answer is : Points D, E and F are not collinear.
Question 4. On a number line, points A, B and C are such that d(A, C) = 10, d(C, B) = 8. Find d(A, B) considering all possibilities.
d(A, C) = 10, d(C, B) = 8 ….(given)
Possibility 1 :
C lies between A and B, i.e. A—C —B.

d(A, B) = d(A, C) + d(C, B) ..(A—C—B)
∴ d(A, B) = 10 + 8
∴ d(A, B) = 18
When C lies between A and B, d(A, B) = 18
Possibility 2 :
B lies between A and C, i.e. A—B —C.
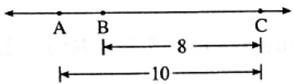
d(A, B) + d(B, C) = d(A, C)
∴ d(A, B) + 8 = 10
∴ d(A, B) = 10 — 8
∴ d(A, B) = 2
When B lies between A and C, d(A, B) =2
Answer is : d(A, B) =18 or 2.
Question 5. Points X, Y, Z are collinear such that d(X, Y) = 17, d(Y, Z) = 8, find d(X, Z) .
d(X, Y) = 17; d(Y, Z) = 8 …..(Given)
Points X, Y and Z are collinear.
Possibility 1 :
Point Z lies between points X and Y i.e. X—Z—Y.

d(X, Z) + d(Z, Y) = d(X, Y) ….(X—Z—Y)
∴ d(X, Z) + 8 = 17
∴ d(X, Z) = 17 — 8
∴ d(X, Z) = 9
Possibility 2 :
Point Y lies between points X and Z i.e. X—Y—Z.

d(X, Z) = d(X, Y) + d(Y, Z) ….(X—Y—Z)
∴ d(X, Z) = 17 + 8
∴ d(X, Z) = 25
Answer is : d(X, Z) = 25 or 9.
Question 6. Sketch proper figure and write the answers of the following questions.
(i) If A—B—C and l(AC) = 11, l(BC) = 6.5, then l(AB) =?

l(AC) = 11, l(BC) = 6.5
l(AB) + l(BC) = l(AC) …..(A—B—C)
∴ l(AB) + 6.5 = 11
∴ l(AB) = 11 — 6.5
∴ l(AB) = 4.5
Answer is : l(AB) = 4.5.
(ii) If R—S—T and l(ST) = 3.7, l(RS) = 2.5, then l(RT) =?

l(RS) = 2.5, l(ST) = 3.7
l(RS) + l(ST) = l(RT) ...(R—S—T)
∴ 2.5 + 3.7 = l(RT)
∴ l(RT) = 6.2
Answer is : l(RT) = 6.2
(iii) If X—Y—Z and l(XZ) = 3 , l(XY) = , then l(YZ) = ?
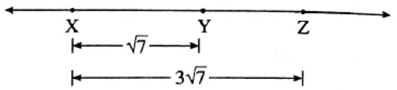
l(XY) = \(\sqrt{7}\), l(XZ) = 3\(\sqrt{7}\)
l(XY) + l(YZ) = l(XZ) ……(X—Y~Z)
∴ \(\sqrt{7}\) + l(YZ) = 3\(\sqrt{7}\)
∴ l(YZ) = 3\(\sqrt{7}-\sqrt{7}\)
∴ l(YZ) = 2\(\sqrt{7}\)
Answer is : l(YZ) = 2\(\sqrt{7}\)
Question 7. Which figure is formed by three non—collinear points ?
A triangle is formed by three non—collinear points.
Practice set 1.2 :
Question 1. The following table shows points on a number line and their co—ordinates. Decide whether the pair of segments given below the table are congruent or not.
| Point | A | B | C | D | E |
| Co—ordinate | —3 | 5 | 2 | —7 | 9 |
(i) seg DE and seg AB
seg DE :
l(DE) = d(D, E)
Coordinate of point D is — 7
Coordinate of point E is 9
9 > — 7
∴ d(D, E) = 9 — ( — 7)_
∴ d(D,E) = 9 + 7,
∴ d(D,E) = 16
∴ l(DE) = 16 …..(1)
seg AB :
l(AB) = d(A, B)
Coordinate of pointA is —3,
Coordinate of point B is 5
5 > —3
∴ d(A,B)=5—(—3)
∴ d(A, B) = 5 + 3
∴ d(A,B) = 8
∴ l(AB) = 8 ……(2)
∴ l(DE) ≠ l(AB) ……[From (1) and (2)]
Answer is : seg DE and seg AB are not congruent.
(ii) seg BC and seg AD
seg BC :
l(BC) = d(B, C)
Coordinate of point B is 5
Coordinate of point C is 2
5 > 2
∴ d(B, C) = 5 — 2
∴ d(B, C) = 3
∴ l(BC) = 3 …....(1)
seg AD :
l(AD) = d(A, D)
Coordinate of point A is —3
Coordinate of point D is —7
—3 > —7
∴ d(A,D) = —3 — (—7)
∴ d(A,D) = —3 + 7
∴ d(A, D) = 4
l(AD) = 4 ……..(2)
l(BC) ≠ l(AD) ……[From (1) and (2)]
Answer is : seg BC is not congruent to seg AD.
(iii) seg BE and seg AD
seg BE :
l(BE) = d(B, E)
Coordinate of point B is 5
Coordinate ofpoint E is 9
9 > 5
∴ d(B, E) = 9 — 5
∴ d(B, E) = 4
∴ l(BE) = 4 ...(1)
seg AD :
l(AD) = d(A, D)
Coordinate ofp0intA is — 3
Coordinate ofpoint D is —7
—3 > —7
d(A,D) = —3 —(—7)
∴ d(A,D) = —3 + 7
∴ d(A, D) = 4
∴ l(AD) = 4 …..(2)
l(BE) = l(AD) …..[From (1) and (2)]
seg BE ≅ seg AD
Answer is : seg BE and seg AD are congruent.
Question 2. Point M is the midpoint of seg AB. If AB = 8 then find the length of AM.
l(AB) = 8 ……(Given)
l(AM) = \(\frac{1}{2}\) l(AB) …..(M is the midpoint of seg AB)
∴ l(AM) = \(\frac{1}{2}\) × 8
∴ l(AM) = 4
Answer is : l(AM) = 4
Question 3. Point P is the midpoint of seg CD. If CP = 2.5, find l(CD).
l(CP) = 2.5 …..(Given)
l(CD) = 2l(CP) …..(P is the midpoint of seg CD)
∴ l(CD) = 2 × 2.5
∴ l(CD) = 5
Answer is : l(CD) = 5.
Question 4. If AB = 5 cm, BP = 2 cm and AP = 3.4 cm, compare the segments.
Given : AB = 5 cm, BP = 2 cm, AP = 3.4 cm
5 > 3.4 > 2
∴ AB > AP > BP
∴ segAB > segAP > scg BP.
Question 5. Write the answers to the following questions with reference to figure

(i) Write the name of the opposite ray of ray RP
Ray RS or Ray RT is the ray opposite to ray RP.
(ii) Write the intersection set of ray PQ and ray RP.
Ray PQ is the intersection set of ray PQ and ray RP.
(iii) Write the union set of seg PQ and seg QR.
Line PQ or line QR is the union set of ray PQ and ray QR.
(iv) State the rays of which seg QR is a subset.
Seg QR is a subset of ray RQ, ray SQ, ray TQ, ray QR, ray QS, ray QT.
(v) Write the pair of opposite rays with common end point R.
Ray RP and ray RS is the pair of opposite rays with common endpoint R.
(vi) Write any two rays with common end point S.
Ray SR and ray ST are two rays with common endpoint S.
(vii) Write the intersection set of ray SP and ray ST.
The intersection of ray SP and ray ST is point S.
Question 6. Answer the questions with the help of figure.

(i) State the points which are equidistant from point B.
- Point C and point A are equidistant from point B as both of the points are at a distance of 2 units from B.
· Also, Point D and point P are equidistant from point B as both of the points are at a distance of 4 units from B.
(ii) Write a pair of points equidistant from point Q.
- Point L and point U is the pair of points equidistant from point Q as both of the points are at a distance of 1 unit from point Q.
- Also, Point P and point R is the pair of points equidistant from point Q as both of the points are at a distance of 2 units from point Q.
(iii) Find d(U,V), d(P,C), d(V,B), d(U, L).
For d(U, V):
Coordinate of point U is — 5
Coordinate of point V is 5
5 > —5
d(U, V) = 5 - (—5)
d(U, V) = 5 + 5
d(U, V) = 10
Answer is : d(U, V) = 10.
For d(P, C) :
Coordinate of point P is —2
Coordinate of point C is 4
4 > — 2
d(P, C) = 4—(—2)
d(P, C) = 4 + 2
d(P, C) = 6
Answer is : d(P, C) = 6.
For d(V, B) :
Coordinate of point V is 5
Coordinate of point B is 2
5 > 2
a’(V, B)=5 —2
d(V, B) = 3
Answer is : d(V, B) = 3
For d(U, L) :
Coordinate of point U is —5
Coordinate of point L is —3
—3 > —5
d(U, L) = -3 -(-5)
fl'(U,L) = -3 + 5
d(U, L) = 2
Answer is : d(U, L) = 2.
Practice set 1.3 :
Question 1. Write the following statements in ‘if -then’ form :
(i) The opposite angles of a parallelogram are congruent.
If a quadrilateral is a parallelogram, then its opposite angles are congruent.
(ii) The diagonals of a rectangle are congruent.
If a quadrilateral is a rectangle, then its diagonals are congruent.
(iii) In an isosceles triangle, the segment joining the vertex and the midpoint of the haw is perpendicular to the base.
If a triangle is an isosceles triangle, then the segment joining the vertex and the midpoint of the base is perpendicular to the base.
Question 2. Write converses of the following statements :
(i) The alternate angles formed by two parallel lines and their transversal are congruent.
If alternate angles made by two lines and its transversal are congruent, then the lines are parallel.
(ii) lf a pair of the interior angles made by a transversal of two lines are supplementary then the lines are parallel.
If two parallel lines are intersected by a transversal, then the interior angles so formed are supplementary.
(iii) The diagonals of a rectangle are congruent.
If the diagonals of a quadrilateral are congruent, then that quadrilateral is a rectangle.
Problem set 1 :
Question 1. Select the correct alternative from the answers of the questions given below.
(i) How many mid points does a segment have ?
(A) only one (B) two (C) three (D) many
(A) only one
(ii) How many points are there in the intersection of two distinct lines ?
(A) infinite (B) two (C) one (D) not a single
(C) one
(iii) How many lines are determined by three distinct points?
(A) two (B) three (C) one or three (D) six
(C) one or three
(iv) Find d(A, B), if co-ordinates of A and B are - 2 and 5 respectively.
(A) -2 (B) 5 (C) 7 (D) 3
(C) 7
(v) If P-Q-R and d(P, Q) = 2, d(P, R) = 10, then find d(Q, R).
(A) 12 (B) 8 (C) 96 (D) 20
(B) 8
Question 2. On a number line, co-ordinates of P, Q, R are 3, - 5 and 6 respectively. State with reason whether the following statements are true or false.
(i) d(P, Q) + d(Q, R) = d(P, R)
(ii) d(P, R) + d(R, Q) = d(P, Q)
(iii) d(R, P) + d(P, Q) = d(R, Q)
(iv) d(P, Q) - d(P, R) = d(Q, R)
Given : Coordinate of point Q is -5, Coordinate of point P is 3, Coordinate of point R is 6
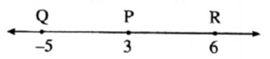
Find d(P, Q) :
Coordinate of point P is 3
Coordinate of point Q is —5
3 > —5
∴ d(P, Q) = 3—(—5)
∴ d(P, Q) = 3 + 5
∴ d(P, Q) = 8
Find d(Q, R) :
Coordinate of point Q is —5
Coordinate of point R is 6
6 > — 5
∴ d(Q, R) = 6 — (—5)
∴ d(Q, R) = 6 + 5
∴ d(Q, R) = 11
Find d(P, R) :
Coordinate of point P is 3
Coordinate of point R is 6
6 > 3
∴ d(P, R) = 6—3
∴ d(P, R) = 3
(i) d(P, Q) + d(Q, R) = 8 + 11
∴ d(P, Q) + d(Q, R) = 19
d(P, R) = 3
∴ d(P, Q) + d(Q, R) ≠ d(P, R)
Answer is : d(P, Q) + d(Q, R) =d(P, R) is a false statement.
(ii) d(P, R) + d(R, Q) = 3 + 11
∴ d(P, R) + d(R, Q) = 14
d(P, Q) = 8
∴ d(P, R) + d(R, Q) ≠ d(P, Q)
Answer is : d(P, R) + d(R, Q) = d(P, Q) is a false statement.
(iii) d(R, P) + d(P, Q) = 3 + 8
∴ d(R, P) + d(P, Q) = 11
d(R, Q) = 11
∴ d(R, P) + d(P, Q) = d(R, Q)
Answer is : d(R, P) + d(P, Q) = d(R, Q) is a true statement.
(iv) d(P, Q) — d(P, R) = 8 — 3
∴ d(P, Q) — d(P, R) = 5
d(Q, R) = 11
∴ d(P, Q) — d(P, R) ≠ d(Q, R)
Answer is : d(P, Q) — d(P, R) =d(Q, R) is a false statement.
Question 3. Co—ordinates of some pairs of points are given below. Hence find the distance between each pair.
(i) 3, 6
Coordinate of the first point = 3
Coordinate of the second point = 6
6 > 3
The distance between the two points
= 6 —3 = 3
Answer is : Distance between the two points is 3.
(ii) — 9, — 1
Coordinate of the first point = —9
Coordinate of the second point = —1
—1 > —9
The distance between the two points
= —1 — (—9)
= — 1 + 9 = 8
Answer is : Distance between the two points is 8
(iii) — 4, 5
Coordinate of the first point = —4
Coordinate of the second point = 5
5 >—4
The distance between the two points
= 5 — (—4) = 5 + 4 = 9
Answer is: Distance between the two points is 9
(iv) 0, — 2
Coordinate of the first point = 0
Coordinate of the second point = —2
0 > —2
The distance between the two points
= 0 — (—2) = 0 + 2 = 2
Answer is : Distance between the two points is 2
(v) x + 3, x — 3
Coordinate of the first point is x + 3
Coordinate of the second point is x — 3
For any real value of x, x + 3 > x — 3
x + 3 > x — 3
The distance between the two points
= (x + 3) — (x — 3)
= x + 3 — x + 3 = 6
Answer is : Distance between the two points is 6.
(vi) — 25, — 47
Coordinate of the first point = —25
Coordinate of the second point = —47
— 25 > — 47
The distance between the two points
= —25 — (—47) = —25 + 47 = 22
Answer is : Distance between the two points is 22
(vii) 80, — 85
Coordinate of the first point = 80
Coordinate of the second point = —85
80 > —85
The distance between the two points
= 80 — (—85) = 80 + 85 = l65
Answers is: Distance between the two points is 165
Question 4. Co—ordinate of point P on a number line is — 7. Find the co—ordinates of points on the number line which are at a distance of 8 units from point P.

Let A, having coordinate x, be the point on the left side of P at a distance of 8 from P.
Coordinate of point P is — 7.
— 7 > x
d(A, P) = 8
∴ 8 = —7 — x
∴ x = —7 — 8
x = — 15
Coordinate of point A is — 15.
Let B, having coordinate y, be the point on the right side of P at a distance of 8 from P.
Y > —7,
d(P, B) = 8
∴ 8 = y — (—7)
∴ 8 = y + 7
∴ y = 8 — 7
y = 1
Coordinate of point B is 1.
Ans. Coordinates of points on the number line which are at a distance of 8 units from P are —15 and 1.
Question 5. Answer the following questions.
(i) If A — B — C and d(A,C) = 17, d(B,C) = 6.5 then d(A,B) = ?
d(A, B) + d(B, C) = d(A, C) …..(A — B — C)
d(A, B) + 6.5 = 17
d(A, B) = 17 — 6.5
∴ d(A, B) = 10.5
Answer is: d(A, B) = 10.5.
(ii) If P — Q — R and d(P,Q) = 3.4, d(Q,R)= 5.7 then d(P,R) = ?
d(P, R) = d(P, Q) + d(Q, R) ….( P — Q – R)
d(P, R) = 3.4 + 5.7
d(P, R) = 9.1
Answer is: d(P, R) = 9.1
Question 6. Co—ordinate of point A on a number line is 1. What are the co—ordinates of points on the number line which are at a distance of 7 units from A ?
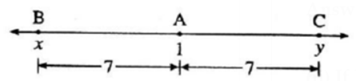
Coordinate of point A is 1.
Let B, having coordinate x, be the point on the left side ofA at a distance of 7 from A.
1 > x, d(A, B) = 7
∴ 7 = 1—x
∴ x = 1 —7 = —6
Coordinate of point B is — 6.
Let C having coordinate y, be the point on the right side of A at a distance of 7 from A.
y > 1, d(A, C) = 7
∴ 7 = y — 1.
∴ y = 7 + l = 8
Coordinate of point C is 8.
Ans. Coordinates of points on number line which are at a distance of 7 units from A are — 6 and 8.
Question 7. Write the following statements in conditional form.
(i) Every rhombus is a square.
If the quadrilateral is a rhombus, then it is a square.
(ii) Angles in a linear pair are supplementary.
If the angles are in a linear pair, then they are supplementary.
(iii) A triangle is a figure formed by three segments.
If the figure is a triangle, then it is formed by three segments.
(iv) A number having only two divisors is called a prime number.
If a number is having only two divisors, then it is called a prime number.
Question 8. Write the converse of each of the following statements.
(i) If the sum of measures of angles in a figure is 1800, then the figure is a triangle.
If the figure is a triangle, then the sum of the measures of the angles is 180°.
(ii) If the sum of measures of two angles is 900 then they are complement of each other.
If two angles are complement of each other, then the sum of the measures of two angles is 90°.
(iii) If the corresponding angles formed by a transversal of two lines are congruent then the two lines are parallel.
If the two lines are parallel, then the corresponding angles formed by a transversal of two lines are congruent.
(iv) If the sum of the digits of a number is divisible by 3 then the number is divisible by 3.
If the number is divisible by 3, then the sum of the digits of the number is also divisible by 3.
Question 9. Write the antecedent (given part) and the consequent (part to be proved) in the following statements.
(i) If all sides of a triangle are congruent then its all angles are congruent.
Antecedent : All sides of a triangle are congruent.
Consequent : Its all angles are congruent.
(ii) The diagonals of a parallelogram bisect each other.
Consider statement in conditional form. ‘If a quadrilateral is a parallelogram, then its diagonals bisect each other.
Antecedent : Quadrilateral is a parallelogram.
Consequent : Diagonals bisect each other.
Question 10*. Draw a labelled figure showing information in each of the following statements and write the antecedent and the consequent.
(i) Two equilateral triangles are similar.
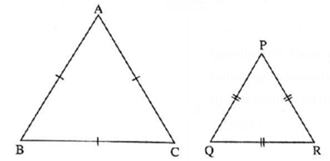
Consider statement in conditional form ‘lf two triangles are equilateral, then they are similar.’
Antecedent : Two triangles are equilateral. i.e. Δ ABC and Δ PQR are equilateral.
Consequent : Triangles are similar.
i.e. Δ ABC ~ Δ PQR.
(ii) If angles in a linear pair are congruent then each of them is a right angle.

Antecedent : Angles in a linear pair arc congruent. i.e. ∠ ABC ≅ ∠CBD
Consequent : Each of the angles is a right angle.
i.e. ∠ ABC = ∠ CBD = 90°.
(iii) If the altitudes drawn on two sides of a triangle are congruent then those two sides are congruent.
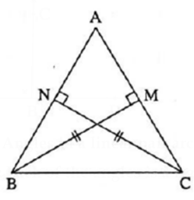
Antecedent : Altitudes drawn on two sides of a triangle are congruent.
i.e. in Δ ABC,
seg BM ⊥ side AC, A—M—C
seg CN ⊥ side AB, A—N—B
seg BM ≅ seg CN.
Consequent : Those two sides are congruent.
i.e. side AB ≅ side AC.
PDF-Notes,Solution,Text Book
Main Page : – Maharashtra Board Class 9th-Mathematics – All chapters notes, solutions, videos, test, pdf.
Next Chapter : Chapter-2-Parallel Lines – Online Solutions