Notes
Perpendicular bisector Theorem :
- Every point on the perpendicular bisector of a segment is equidistant from its endpoints.
- Every point equidistant from the endpoints of a segment is on the perpendicular bisector of that segment.
Constructions of triangles :
To construct a triangle, three conditions are required. Out of three sides and three angles of a triangle two parts and some additional information about them is given, then we can construct a triangle using them.
Construction I :
To construct a triangle when its base, an angle adjacent to the base and the sum of the lengths of remaining sides is given.
Example : Construct Δ ABC in which BC = 6.3 cm, ∠B = 75° and AB + AC = 9 cm.
Solution : Let us first draw a rough figure of expected triangle.
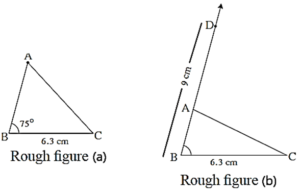
Explanation :
As shown in the rough figure, first we draw seg BC = 6.3 cm of length.
On the ray making an angle of 75° with seg BC, mark point D such that
BD = AB + AC = 9 cm
Now we have to locate point A on ray BD.
BA + AD = BA + AC = 9
∴ AD = AC
∴ point A is on the perpendicular bisector of seg CD.
∴ the point of intersection of ray BD and the perpendicular bisector of seg CD is point A.
Steps of construction :
(1) Draw seg BC of length 6.3 cm.
(2) Draw ray BP such that m∠ PBC = 75°.
(3) Mark point D on ray BP such that d(B,D) = 9 cm
(4) Draw seg DC.
(5) Construct the perpendicular bisector of seg DC .
(6) Name the point of intersection of ray BP and the perpendicular bisector of CD as A.
(7) Draw seg AC.
Δ ABC is the required triangle.
Construction II :
To construct a triangle when its base, angle adjacent to the base and the difference between the remaining sides is given.
Example 1 : Construct Δ ABC such that BC = 7.5 cm, ∠ABC = 40°, AB - AC = 3 cm.
Explanation :
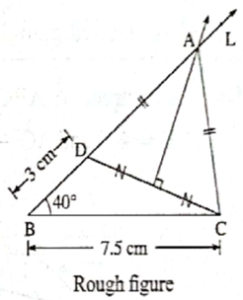
As shown in the rough figure, first we draw seg BC of length 7.5 cm. We draw ray BL such that ∠LBC = 40°.
Take a point D on ray BL such that BD = 3 cm. Now, we have to locate point A on ray BL.
AB = AD + BD ... (A-D-B)
∴ AB = AD + 3 cm ... (BD = 3 cm)
∴ AB -AD = 3 cm ... (1)
Now, AB - AC = 3 cm ... (Given) ... (2)
∴ AB - AD = AB – AC ... [From (1) and (2)]
∴ AD = AC
∴ point A is equidistant from the endpoints D and C of seg DC.
∴ point A lies on the perpendicular bisector of seg DC ... (Perpendicular bisector theorem)
∴ point A is the point of intersection of ray BL and perpendicular bisector of seg DC.
Steps of construction :
(1) Draw seg BC of length 7.5 cm.
(2) Draw ray BL such that ∠LBC = 40°.
(3) Take point D on ray BL such that BD = 3 cm.
(4) Construct the perpendicular bisector of seg CD.
(5) Name the point of intersection of ray BL and the perpendicular bisector of seg CD as A.
(6) Draw seg AC.
Δ ABC is the required triangle.
Example 2. Construct Δ ABC in which side BC = 7 cm, ∠B = 40° and AC - AB = 3 cm.
Explanation :
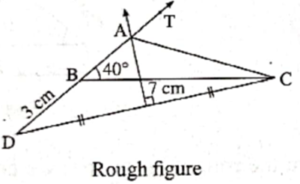
As shown in the rough figure, first we draw seg BC of length 7 cm.
Now, AC > AB
We draw ray BT such that ∠TBC = 40°.
Now, we have to locate point A on ray BT.
Take a point D on the ray opposite of ray BT such that BD = 3 cm.
Now.
AD = AB + BD ... (A-B-D)
∴ AD = AB + 3 cm
∴ AD -AB = 3 cm ... (1)
AC – AB = 3 cm ... (Given) ... (2)
∴ AD - AB = AC – AB ... [From (1) and (2)]
∴ AD = AC
∴ point A is equidistant from the points D and C.
∴ point A lies on the perpendicular bisector of seg DC ... (Perpendicular bisector theorem)
∴ point A is the point of intersection of ray BA and perpendicular bisector of seg DC.
Steps of construction :
(1) Draw seg BC of length 7 cm.
(2) Draw ray BT such that ∠TBC = 40°.
(3) Take point D on the opposite ray BS of ray BT such that BD = 3 cm.
(4) Construct perpendicular bisector of seg DC.
(5) Name the point of intersection of ray BT and the perpendicular bisector of seg DC as A.
(6) Draw seg AC.
Δ ABC is the required triangle.
Construction III :
To construct a triangle, if its perimeter, base and the angles which include the base are given.
Ex. Construct Δ ABC such that AB + BC + CA = 11.3 cm, ∠B = 70°, ∠C = 60°.
Solution : Let us draw a rough figure.
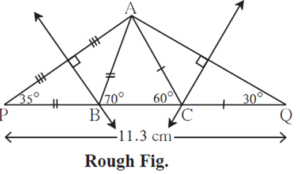
Explanation : As shown in the figure, points P and Q are taken on line BC such that,
PB = AB, CQ = AC
∴ PQ = PB + BC + CQ = AB + BC +AC = 11.3 cm.
Now in DPBA, PB = BA
∴ ∠APB = ∠PAB and ∠APB + ∠PAB = exterior angle ABC = 70° ......(theorem of remote interior angles)
∴ ∠APB = ∠PAB = 35° Similarly, ∠CQA = ∠CAQ = 30°
Now we can draw Δ PAQ, as its two angles and the included side is known.
Since BA = BP , point B lies on the perpendicular bisector of seg AP.
Similarly, CA = CQ, therefore point C lies on the perpendicular bisector of seg AQ
∴ by constructing the perpendicular bisectors of seg AP and AQ we can get points
B and C, where the perpendicular bisectors intersect line PQ.
Steps of construction
(1) Draw seg PQ of 11.3 cm length.
(2) Draw a ray making angle of 35° at point P.
(3) Draw another ray making an angle of 30° at point Q.
(4) Name the point of intersection of the two rays as A.
(5) Draw the perpendicular bisector of seg AP and seg AQ. Name the points as B and C respectively where the perpendicular bisectors intersect line PQ.
(6) Draw seg AB and seg AC.
Δ ABC is the required triangle.
We reply to valid query.