Notes
Parallel lines : The lines which are coplanar and do not intersect each other are called parallel lines.
Transversal and intercept :
Transversal : A line intersecting two other coplanar lines in two distinct points is called a transversal of the two lines.
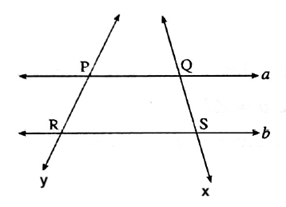
- In the figure, line a and line b are the transversal of lines x and y.
- Line x and line y are the transversals of lines a and b.
Intercept : A segment cut off by a transversal on two distinct lines is called an intercept.
In the above figure, seg PQ is the intercept made by the transversal a on the lines x and y.
Seg PR is the intercept made by the transversal y on the lines a and b.
Angles formed by the transversal :
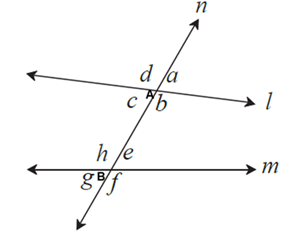
In the figure, line n is the transversal of lines l and m.
∠a, ∠b, ∠c and ∠d are formed at the point A.
∠e, ∠f, ∠g and ∠h are formed at the point B.
Thus, eight angles are formed. Of them, one side or ray of each angle is contained in the transversal.
Here, in all 8 angles are formed. Pairs of angles formed out of these angles are as follows :
Pairs of corresponding angles :
(i) ∠d, ∠h (ii) ∠a, ∠e (iii) ∠c, ∠g (iv) ∠b, ∠f
Pairs of alternate interior angles :
(i) ∠c, ∠e (ii) ∠b, ∠h
Pairs of alternate exterior angles :
(i) ∠d, ∠f (ii) ∠a, ∠g
Pairs of interior angles on the same side of the transversal :
(i) ∠c, ∠h (ii) ∠b, ∠e
Some important properties :
- When two lines intersect, the pairs of opposite angles formed are congruent.
- The angles in a linear pair are supplementary.
- When one pair of corresponding angles is congruent, then all the remaining pairs of corresponding angles are congruent.
- When one pair of alternate angles is congruent, then all the remaining pairs of alternate angles are congruent.
- When one pair of interior angles on one side of the transversal is supplementary, then the other pair of interior angles is also supplementary.
Interior angle theorem :
Theorem : If two parallel lines are intersected by a transversal, the interior angles on either side of the transversal are supplementary.
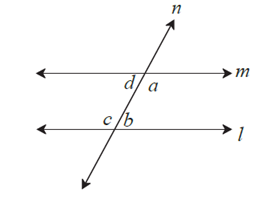
Given : line l || line m and line n is their transversal.
Hence as shown in the figure
∠a, ∠b are interior angles formed on one side and
∠c, ∠d are interior angles formed on other side of the transversal.
To prove : ∠a + ∠b = 180°
∠d + ∠c = 180°
Proof : Three possibilities arise regarding the sum of measures of ∠a and ∠b.
(i) ∠a + ∠b < 180° (ii) ∠a + ∠b > 180° (iii) ∠a + ∠b = 180°
Let us assume that the possibility (i) ∠a + ∠b < 180° is true.
Then according to Euclid’s postulate, if the line l and line m are produced will intersect each other on the side of the transversal where ∠a and ∠b are formed.
But line l and line m are parallel lines ..........given
∴ ∠a + ∠b < 180° impossible ..........(I)
Now let us suppose that ∠a + ∠b > 180° is true.
∴ ∠a + ∠b >180°
But ∠a + ∠d = 180°
and ∠c + ∠b = 180° . . . . . angles in linear pairs
∴ ∠a + ∠d + ∠b + ∠c = 180° +180° = 360°
∴ ∠c + ∠d = 360° - (∠a + ∠b)
If ∠a + ∠b >180° then [360° - (∠a + ∠b)] < 180°
∴ ∠c + ∠d < 180°
∴ In that case line l and line m produced will intersect each other on the same side of the transversal where ∠c and ∠d are formed.
∴ ∠c + ∠d < 180 is impossible.
That is ∠a + ∠b >180° is impossible...... (II)
∴ the remaining possibility,
∠a + ∠b = 180° is true......from (I) and (II)
∴ ∠a + ∠b = 180° Similarly, ∠c + ∠d = 180°
Note that, in this proof, because of the contradictions we have denied the possibilities ∠a + ∠b >180° and ∠a + ∠b <180°.
Therefore, this proof is an example of indirect proof.
Corresponding angles and alternate angles theorems :
Theorem : The corresponding angles formed by a transversal of two parallel lines are of equal measure.
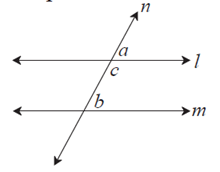
Given : line l || line m line n is a transversal.
To prove : ∠a = ∠b
Proof : ∠a + ∠c = 180° ........(I) angles in linear pair
∠b + ∠c = 180° ..............(II) property of interior angles of parallel lines
∠a + ∠c = ∠b + ∠c .......from (I) and (II)
∴ ∠a = ∠b
Theorem : The alternate angles formed by a transversal of two parallel lines are of equal measures.
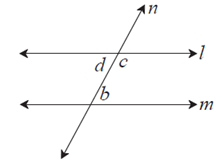
Given : line l || line m line n is a transversal.
To prove : ∠d = ∠b
Proof : ∠d + ∠c = 180°................(I) angles in linear pair
∠c + ∠b = 180° ..............(II) property of interior angles of parallel line
∠d + ∠c = ∠c + ∠b................from (I) and (II)
∴ ∠d = ∠b
Use of properties of parallel lines :
Let us prove a property of a triangle using the properties of angles made by a transversal of parallel lines.
Theorem : The sum of measures of all angles of a triangle is 180°.
Given : Δ ABC is any triangle.
To prove : ∠ABC + ∠ACB + ∠BAC = 180°.
Construction : Draw a line parallel to seg BC and passing through A. On the line take points P and Q such that, P - A - Q.
Proof : Line PQ || line BC and seg AB is a transversal.
∴ ∠ABC = ∠PAB.......alternate angles.....(I)
line PQ || line BC and seg AC is a transversal.
∴ ∠ACB = ∠QAC.......alternate angles.....(II)
∴ From I and II ,
∠ABC + ∠ACB = ∠PAB + ∠QAC . . . (III)
Adding ∠BAC to both sides of (III).
∠ABC + ∠ACB + ∠BAC = ∠PAB + ∠QAC + ∠BAC
= ∠PAB + ∠BAC + ∠QAC
= ∠PAC + ∠QAC ...(Q∠PAB + ∠BAC = ∠PAC)
= 180° ...Angles in linear pair
That is, sum of measures of all three angles of a triangle is 180°.
Tests for parallel lines :
Whether given two lines are parallel or not can be decided by examining the angles formed by a transversal of the lines.
- If the interior angles on the same side of a transversal are supplementary then the lines are parallel.
- If one of the pairs of alternate angles is congruent then the lines are parallel.
- If one of the pairs of corresponding angles is congruent then the lines are parallel.
Interior angles test :
Theorem : If the interior angles formed by a transversal of two distinct lines are supplementary, then the two lines are parallel.
Given : Line XY is a transversal of line AB and line CD.
∠BPQ + ∠PQD = 180°
To prove : line AB || line CD
Proof : We are going to give an indirect proof.
Let us suppose that the statement to be proved is wrong. That is, we assume, line AB and line CD are not parallel, means line AB and CD intersect at point T.
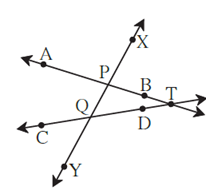
So Δ PQT is formed.
∴ ∠TPQ + ∠PQT + ∠PTQ = 180° ..........sum of angles of a triangle
but ∠TPQ + ∠PQT = 180° ...........given
That is the sum of two angles of the triangle is 180°.
But sum of three angles of a triangle is 180°.
∴ ∠PTQ = 0°.
∴ line PT and line QT means line AB and line CD are not distinct lines.
But, we are given that line AB and line CD are distinct lines.
∴ we arrive at a contradiction.
∴ our assumption is wrong. Hence line AB and line CD are parallel.
Thus it is proved that if the interior angles formed by a transversal are supplementary, then the lines are parallel.
This property is called interior angles test of parallel lines.
Alternate angles test :
Theorem : If a pair of alternate angles formed by a transversal of two lines is congruent then the two lines are parallel.
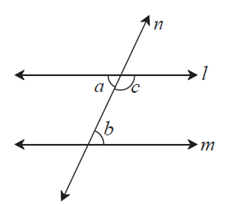
Given : Line n is a transversal of line l and line m.
∠a and ∠b is a congruent pair of alternate angles.
That is, ∠a = ∠b
To prove : line l || line m
Proof : ∠a + ∠c = 180° . ....angles in linear pair
∠a = ∠b .......... given
∴ ∠b + ∠c = 180°
But ∠b and ∠c are interior angles on the same side of the transversal.
∴ line l || line m ....... interior angles test
This property is called the alternate angles test of parallel lines.
Corresponding angles Test :
Theorem : If a pair of corresponding angles formed by a transversal of two lines is congruent then the two lines are parallel.
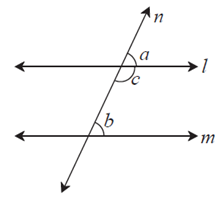
Given : Line n is a transversal of line l and line m.
∠a and ∠b is a congruent pair of corresponding angles.
That is, ∠a = ∠b
To prove : line l || line m
Proof : ∠a + ∠c = 180° ..........angles in linear pair
∠a = ∠b .......... given
∴ ∠b + ∠c = 180°
That is a pair of interior angles on the same side of the transversal is congruent.
∴ line l || line m ..........interior angles test
This property is called the corresponding angles test of parallel lines.
Corollary I : If a line is perpendicular to two lines in a plane, then the two lines are parallel to each other.
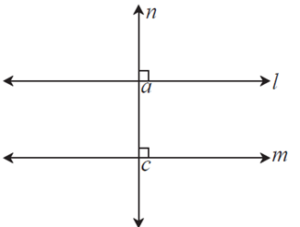
Given : Line n ⊥ line l and line n ⊥ line m
To prove : line l || line m
Proof : line n ⊥ line l and line n ⊥ line m ...given
∴ ∠a = ∠c = 90°
∠a and ∠c are corresponding angles formed by transversal n of line l and line m.
∴ line l || line m ....corresponding angles test
Corollary II : If two lines in a plane are parallel to a third line in the plane then those two lines are parallel to each other. Write the proof of the corollary.
Given : Lines AB, CD and EF are coplanar such that line AB || line CD and line AB || line EF. Line PT is the transversal intersecting lines AB, CD, EF at points Q, R and S respectively.
To prove : line CD || line EF.
Proof : line AB || line CD ... (Given)
and line PT is the transversal,
∠PQB ≅ ∠QRD ... (Corresponding angles) ... (1)
line AB || line EF and line PT is the transversal. ... (Given)
∴ ∠PQB ≅ ∠QSF ... (Corresponding angles) ... (2)
∴ ∠QRD ≅ ∠QSF ... [From (1) and (2)]
i.e. ∠QRD ≅ ∠RSF ... (Q-R-S) ... (3)
∴ line CD || line EF ... (Corresponding angles test for parallel lines)