Notes
Introduction :
Recall :
Linear equations in one variable. e.g. m + 3 = 5, 3y + 8 = 22, etc.
Problems involving one variable :
(i) What should be added to 11 to get 20?
11 + x = 20
(ii) Which number should be subtracted from 11 to get 5 ?
11 – x = 5
In all above equations, degree of the variable is 1. These are called as Linear equations.
Linear equations in two variables :
Examples : Find two numbers whose sum is 14.
Using variables x and y for the two numbers, we can form the equation x + y = 14 .
This is an equation in two variables.
Similarly, x + 2y = 9; 3x − 7y = 1, etc. involve two variables x and y each having degree (index) 1.
We can find many values of x and y satisfying the condition.
These are known as linear equations in two variables.
Two or more different linear equations in two variables, having the same variables, taken together form a system of linear equations in two variables. This system is known as simultaneous equations.
Activity : On the glasses of following spectacles, write numbers such that
(1) Their sum is 37 and difference is 11
Let the bigger number be x and smaller number be y.
Then we get the equations
x + y = 37 …..(i)
x – y = 11 ……(ii)
Solution of equation (i) : (19, 18), (20, 17) , (21, 16), (22, 15), (23, 14) (24, 13)….
Solution of equation (ii) : (12, 1), (13, 2)… (24, 13), (25, 14) …
Here (24,13) is the only common solution of both the equations. This solution satisfies both the equations.
Answer is :
Elimination method of solving simultaneous equations :
In this method, we first make the coefficients of any one variable in both the equations numerically equal by multiplying the equations by suitable constants. Then
either by adding or subtracting new equations, we eliminate one variable.
So we get a linear equation in one variable.
Solving it, we get the value of one variable.
Substituting this value in any one of the given equations, we get the value of the other variable.
General form of Linear Equation in Two Variables :
The general form of the linear equation in two variables is ax + by + c = 0, where a, b, c are real numbers and a ≠ 0, b ≠ 0 at the same time.
Q.1. Solve the following equations
3x + y = 5........... (I)
2x + 3y = 1........(II)
Solution :
To eliminate one of the variables, we observe that in both equations, not a single
coefficient is equal or opposite number.
Hence we will make one of them equal.
Multiply both sides of the equation (I) by 3.
∴ 3x × 3 + 3 × y = 5 × 3
∴ 9x + 3y = 15 .......(III)
2x + 3y = 1 .......(II)
Now subtracting eqn (II) from eqn (III)
9x + 3y = 15
+ 2x + 3y = 1
− − −
_____________
7x = 14
x = 2
Substituting x = 2 in one of the equations.
2x + 3y = 1
∴ 2 × 2 + 3y = 1
∴ 4 + 3y = 1
∴ 3y = −3
∴ y = −1
Verify that (2, −1) satisfies the second equation.
Q.2. 3x − 4y −1 5 = 0 and y + x + 2 = 0. Can these equations be solved by eliminating x ? Is the solution same ?
Solution :
Yes. Multiply y + x + 2 = 0 by − 3.
−3y − 3x – 6 = 0 i.e., − 3y − 3x = 6 …..(i)
3x − 4y = 15 …..(i)
− 3x – 3y = 6 …..(ii)
Adding equation (i) & (ii)
−7y = 21
Solving these equations, y = −3 and x = 1.
Substitution method of solving simultaneous equations :
In this method, we find the value of one variable in terms of the other, from any one of the given equations and substitute the value in the other equation.
So we get a linear equation in one variable. As explained in method of elimination by equating the coefficients by substitution, we can solve the equations.
Q.1. Solve 8x + 3y = 11 ; 3x – y = 2
Solution :
8x + 3y = 11.................. (I)
3x – y = 2.......................(II)
In Equation (II), it is easy to express y in terms of x.
3x – y = 2
3x – 2 = y
Substituting y = 3x −2 in equation (I).
8x + 3y = 11
∴ 8x + 3(3x − 2) = 11
∴ 8x + 9x − 6 = 11
∴ 17x – 6 = 11
∴ 17x = 11 + 6 = 17
∴ x = 1
Now, substituting this value of x in the equation y = 3x – 2.
y = 3 × 1 – 2
∴ y = 1
∴ (1, 1) is the solution of the given equations
Word problems based on simultaneous equations :
Solve the problem, applying the following steps :
(1) Read the given word problem carefully and try to understand it.
(2) From the given information, use proper variables for given quantities
(3) Form the mathematical statements from above variables
(4) Use suitable method to solve the equations
(5) Find the solution
(6) Verify your result.
(7) Write the answer.
Word Problems of various types :
- Problems regarding age.
- Problems regarding numbers.
- Problems based on fractions.
- Problems based on money transactions.
- Problems based on geometrical properties
- Problems based on speed, distance, time.
Q.1. Sum of two numbers is 103. If greater number is divided by smaller number then the quotient is 2 and the remainder is 19. Then find the numbers.
Solution :
Step 1 : To understand the given problem.
Step 2 : Use proper variables for given quantities. Also note the rule
dividend = divisor × quotient + remainder.
Let the greater number be x and the smaller number be y
Step 3 : Given information : Sum of the numbers = 103
x + y = 103 is the first equation.
By dividing greater number by smaller numbers quotient is 2 and remainder is 19.
x = 2 × y + 19 ...(dividend = divisor × quotient + remainder)
x – 2y = 19 is the second equation.
Step 4 : Let us find the solution of the equations.
x + y = 103 ................(I)
x – 2y = 19 ................(II)
Subtracting eqn. (II) from eqn. (I)
x + y = 103
x – 2y = 19
– + −
_____________
0 + 3y = 84
∴ y = 28
Step 5 : Substituting value of y in equation x + y = 103.
∴ x + 28 = 103
∴ x = 103 – 28
∴ x = 75
Step 6 : Given numbers are 75 and 28.
Q.2. The population of a certain town was 50,000. In a year, male population was increased by 5% and female population was increased by 3%. Now the population became 52020. Then what was the number of males and females in the previous year?
Solution :
Let the number of males in previous year be x, number of females be y
By first condition x + y = 50000 .......(I)
Male population increased by 5% ∴ number of males = \(\frac{105}{100}\)x
Female population increased by 3% ∴ number of females = \(\frac{103}{100}\)y.
From second condition \(\frac{105}{100}\)x + \(\frac{103}{100}\)y = 52020
105x + 103y = 5202000 .......(II)
Multiplying equation (I) by 103
103x + 103y = 5150000 .......(III)
Subtracting equation (III) from equation (II) .
2x = 5202000 − 5150000
2x = 52000
∴ number of males = x = 26000 ∴ number of females = y = 24000
Q.3. There are instructions written near the arrows in the following diagram. From this information form suitable equations and write in the boxes indicated by arrows. Select any two equations from these boxes and find their solutions. Also verify the solutions. By taking one pair of equations at a time, how many pairs can be formed ? Discuss the solutions for these pairs.
Solution :
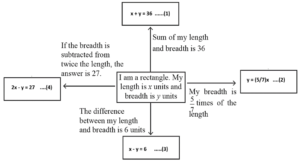
Here, we have following pairs of equations. [All the four equations are for the same rectangle.]
(1) Equations (1) and (2)
(2) Equations (1) and (3)
(3) Equations (1) and (4)
(4) Equations (2) and (3)
(5) Equations (2) and (4)
(6) Equations (3) and (4)
Solution of each pair : length 21 units; breadth 15 units.