Electrostatics
Maharashtra Board-Class-12th-Physics-Chapter-8
Solutions
Q (1) Choose the correct option
(i) A parallel plate capacitor is charged and then isolated. The effect of increasing the plate separation on charge, potential, capacitance respectively are
(A) Constant, decreases, decreases
(B) Increases, decreases, decreases
(C) Constant, decreases, increases
(D) Constant, increases, decreases
(A) Constant, decreases, decreases
(ii) A slab of material of dielectric constant k has the same area A as the plates of a parallel plate capacitor and has thickness (3/4d), where d is the separation of the plates. The change in capacitance when the slab is inserted between the plates is
(A) C = \(\frac{ε_0A}{d}(\frac{k+3}{4k})\)
(B) C = \(\frac{ε_0A}{d}(\frac{2k}{k+3})\)
(C) C = \(\frac{ε_0A}{d}(\frac{k+3}{2k})\)
(D) C = \(\frac{ε_0A}{d}(\frac{4k}{k+3})\)
(D) C = \(\frac{ε_0A}{d}(\frac{4k}{k+3})\)
(iii) Energy stored in a capacitor and dissipated during charging a capacitor bear a ratio.
(A) 1:1
(B) 1:2
(C) 2:1
(D) 1:3
(A) 1:1
(iv) Charge +q and -q are placed at points A and B respectively which are distance 2L apart. C is the mid point of A and B. The work done in moving a charge +Q along the semicircle CRD as shown in the figure below is
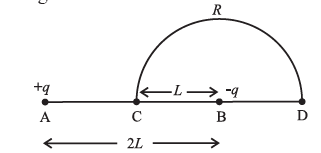
(A) \(-\frac{Qq}{6πε_0L}\)
(B) \(\frac{Qq}{2πε_0L}\)
(C) \(\frac{Qq}{6πε_0L}\)
(D) \(-\frac{Qq}{4πε_0L}\)
(A) \(-\frac{Qq}{6πε_0L}\)
(v) A parallel plate capacitor has circular plates of radius 8 cm and plate separation 1mm. What will be the charge on the plates if a potential difference of 100 V is applied?
(A) 1.78 × 10-8 C
(B) 1.78 × 10-5 C
(C) 4.3 × 104 C
(D) 2 × 10-9 C
(A) 1.78 × 10-8 C
Q2. Answer in brief.
(i) A charge q is moved from a point A above a dipole of dipole moment p to a point B below the dipole in equatorial plane without acceleration. Find the work done in this process.
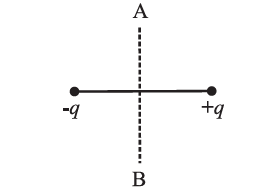
The equatorial plane of an electric dipole is an equipotential with V = 0. Therefore, the no work is done in moving a charge between two points in the equatorial plane of a dipole.
(ii) If the difference between the radii of the two spheres of a spherical capacitor is increased, state whether the capacitance will increase or decrease.
The capacitance of a spherical capacitor is C = 4πε0 \((\frac{ab}{b-a})\) where a and b are the radii of the concentric inner and outer conducting shells
Hence, the capacitance decreases if the difference b—a is increased. '
(iii) A metal plate is introduced between the plates of a charged parallel plate capacitor. What is its effect on the capacitance of the capacitor?
Suppose the parallel-plate capacitor has capacitance C0, plates of area A and separation d. Assume the metal sheet introduced has the same area A.
Case (1) : Finite thickness t. Free electrons in the sheet will migrate towards the positive plate of the capacitor. Then, the metal sheet is attracted towards whichever capacitor plate is closest and gets stuck to it, so that its potential is the same as that of that plate. The gap between the capacitor plates is reduced to d— t, so that the capacitance increases.
Case (2) : Negligible thickness. The thin metal sheet divides the gap into two of thicknesses d1 and d2 of capacitances C1 = ε0A/d1 and C2 = ε0A/d2 in series.
Their effective capacitance is
C = \(\frac{c_1c_2}{c_1+c_2}=\frac{ε_0A}{d_1+d_2}\) = \(\frac{ε_0A}{d}\) = C0
i.e., the capacitance remains unchanged.
(iv) The safest way to protect yourself from lightening is to be inside a car. Justify.
- There is danger of lightning strikes during a thunderstorm. Because trees are taller than people and therefore closer to the clouds above, they are more likely to get hit by lightning.
- Similarly, a person standing in open ground is the tallest object and more likely to get hit by a lightning.
- But car with a metal body is an almost ideal Faraday cage. When a car is struck by lightning, the charge flows on the outside surface of the car to the ground but the electric field inside remains zero. This leaves the passengers inside unharmed.
(v) A spherical shell of radius b with charge Q is expanded to a radius a. Find the work done by the electrical forces in the process.
Consider a spherical conducting shell of radius r placed in a medium of permittivity s. The mechanical force per unit area on the charged conductor is
F= F/dS = σ2/2ε
where σ is the surface charge density on the conductor. Given the charge on the spherical shell is Q,
σ = Q/4πr2. The force acts outward, normal to the surface.
Suppose the force displaces a charged area element σdS through a small distance dx, then the work done by the force is
dW = Fdx = \((\frac{σ^2}{2ε}ds)dx\)
During the displacement, the area element sweeps out a volume dV = dS.dx.
Since V = \(\frac{4}{3}\)πr2 dV = 4πr2dr
∴ dW = \(\frac{σ^2}{2ε}\)dV = \(\frac{1}{2ε}(\frac{Q}{4πr^2})^2(4πr^2dr)\)
= \(\frac{Q}{8πεr^2}dr\)
Therefore, the work done by the force in expanding the shell from radius r = b to r = a is
W = \(\int dw = \frac{Q}{8πε}\int_b^a \frac{1}{r^2}dr = \frac{Q}{8πε}[-\frac{1}{r}]_b^a\) = \(\frac{Q}{8πε}[\frac{1}{b}-\frac{1}{a}]\)
This gives the required expression for the work done.
(3) A dipole with its charges, -q and +q located at the points (0, —b, 0) and (0 +b, 0) is present in a uniform electric field E. The equipotential surfaces of this field are planes parallel to the YZ planes.
(a) What is the direction of the electric field E?
(b) How much torque would the dipole experience in this field?
(a) Given, the equipotentials of the external uniform electric field are planes parallel to the yz plane, the electric field \(\vec{E} = ±E\hat{i}\) , that is, \(\vec{E}\) is parallel to the x-axis.
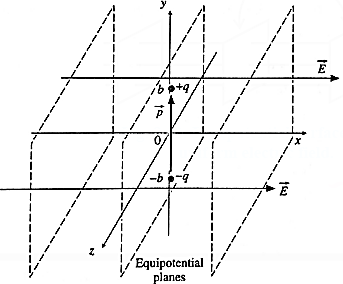
(b) From Fig. the dipole moment, \(\vec{E}\) = q(2b)\(\hat{j}\)
The torque on this dipole,
\(\vec{τ}\) = \(\vec{p}\) x \(\vec{E}\) = 2qb\(\hat{j}\) x (±E\(\hat{i}\) ) = (2qbE)(\(\hat{i}\) x \(\hat{j}\))
Since \(\hat{i}\) x \(\hat{j}\) = \(-\hat{k}\) ,
= (±2qbE)(\(-\hat{k}\)) = (2qbE)(±\(\hat{k}\))
So that the magnitude of the torque is τ = 2qbE.
If \(\vec{E}\) is in the direction of the + x-axis, the torque \(\vec{τ}\) is in the direction of — z-axis, while if \(\vec{E}\) is in the direction of the —x-axis, the torque \(\vec{τ}\) is in the direction of + z-axis.
(4) Three charges -q, +Q and -q are placed at equal distance on straight line. If the potential energy of the system of the three charges is zero, then what is the ratio of Q : q ?
In Fig. the line joining the charges is shown as the x-axis with the origin at the + Q charge.
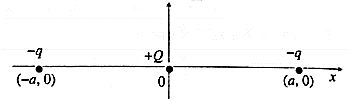
Let q1 = +Q, and q2 = q3 = −q.
Let the two −q charges be at ( −a, 0) and (a, 0), since the charges are given to be equidistant.
r21 = r31 =a and r32 = 2a
The total potential energy of the system of three charges is
U3 = \(\frac{1}{4πε_0}(\frac{q_1q_2}{r_{21}}+\frac{q_1q_3}{r_{31}}+\frac{q_2q_3}{r_{32}})\)
= \(\frac{1}{4πε_0}(\frac{(-q)Q}{a}+\frac{Q(-q)}{a}+\frac{(-q)(-q)}{2a})\)
= \(\frac{1}{4πε_0}(-\frac{2qQ}{a}+\frac{q^2}{2a})\)
Given U3 = 0
∴ \(\frac{2qQ}{a}=\frac{q^2}{2a}\)
∴ Q/q = ¼
This is the required ratio.
(5) A capacitor has some dielectric between its plates and the capacitor is connected to a DC source. The battery is now disconnected and then the dielectric is removed. State whether the capacitance, the energy stored in it, the electric field, charge stored and voltage will increase, decrease or remain constant.
Assume a parallel-plate capacitor, of plate area A and plate separation d is filled with a dielectric of relative permittivity (dielectric constant) k.
Its k capacitance is C = \(\frac{kε_0A}{d}\) …….(1)
If it is charged to a voltage (potential) V, the charge on its plates is Q = CV.
Since the battery is disconnected after it is charged, the charge Q on its plates, and consequently the product CV, remain unchanged.
On removing the dielectric completely, its capacitance becomes from Eq. (1),
C’ = \(\frac{ε_0A}{d}\) = \(\frac{1}{k}C\)
that is, its capacitance decreases by the factor k-
Since C'V’ = CV, its new voltage is
V’ = \(\frac{C}{C'}V\) = kV
so that its voltage increases by the factor k
The stored potential energy, U = \(\frac{1}{2}QV\) so that Q remaining constant, U increases by the factor k.
The electric field, E = V/d, so that E also increases by a factor k.
(6) Find the ratio of the potential differences that must be applied across the parallel and series combination of two capacitors C1 and C2 with their capacitances in the ratio 1:2, so that the energy stored in these two cases becomes the same.
Given : \(\frac{C_1}{C_2}=\frac{1}{2}\) = E, U1 (for parallel) = U2 (for series)
\(\frac{C_1}{C_2}=\frac{1}{2}\) ∴ C2 = 2C1
For the parallel combination of C1 and C2,
CP = C1 + C2 = 3C1
and charged to a potential V1, the energy stored is
U1 = \(\frac{1}{2}\)CPV12 = \(\frac{3}{2}\)C1V12
For the series combination of C1 and C2,
Cs = \(\frac{C_1C_2}{C_1+C_2}\) = \(\frac{2C_1^2}{3C_1^2}\) = \(\frac{2}{3}C_1\)
and charged to a potential V2, the energy stored is
U2 = \(\frac{1}{2}\)CsV22 = \(\frac{1}{3}\)C1V22
∴ for U1 = U2 = \(\frac{3}{2}\)C1V12 = \(\frac{1}{3}\)C1V22
∴ \((\frac{V_1}{V_2})^2=\frac{2}{9}\) ∴ \(\frac{V_1}{V_2}=\frac{\sqrt{2}}{3}=\frac{1.414}{3}\)= 0.471
This gives the required ratio.
(7) Two charges of magnitudes −4Q and +2Q are located at points (2a, 0) and (5a, 0) respectively. What is the electric flux due to these charges through a sphere of radius 4a with its centre at the origin?
The sphere of radius 4a encloses only the negative charge Q1 = −4Q. The positive charge Q2 = + 2Q being located at a distance of 5a from the origin is outside the sphere. Only a part of the electric flux lines originating at Q2 enters the sphere and exits entirely at other points. Hence, the electric flux through the sphere is only due to Q1.
Therefore, the net electric flux through the sphere = Q1/ε0 = −4Q/ε0. The minus sign shows that the flux is directed into the sphere, but not radially since the sphere is not centred on Q1.
(8) A 6 µF capacitor is charged by a 300 V supply. It is then disconnected from the supply and is connected to another uncharged 3µF capacitor. How much electrostatic energy of the first capacitor is lost in the form of heat and electromagnetic radiation ?
Given : C = 6 μF = 6 x 10—6 F = C1, V = 300 V, C2 = 3 μF
The electrostatic energy in the capacitor
= \(\frac{1}{2}\)CV2 = \(\frac{1}{2}\)(6 x 10—6)(300)2
= 3 x 10—6 x 9 x 104 = 0.27 J
The charge on this capacitor,
Q = CV = (6 x 10—6)(300) = 1.8 mC
When two capacitors of capacitances C1 and C2 are connected in parallel, the equivalent capacitance C
=C1 + C2 = 6 + 3 = 9 μF
= 9 x 10—6 F
By conservation of charge, Q = 1.8 C.
∴ The energy of the system = \(\frac{Q^2}{2C}=\frac{(1.8×10^{-3})^2}{2(9×10^{-6})}\) = 0.18 J
The energy lost = 0.27 − 0.18 = 0.09 J = 9 x 10-2 J
(9) One hundred twenty five small liquid drops, each carrying a charge of 0.5 μC and each of diameter 0.1 m form a bigger drop. Calculate the potential at the surface of the bigger drop.
Given: n = 125, q = 0.5 x10−6 C, d=0.1 m
The radius of each small drop, r = d/2 = 0.05 m
The volume of the larger drop being equal to the volume of the n smaller drops, the radius of the larger drop is
R = \(\sqrt[3]{n}r\) = \(\sqrt[3]{125}(0.05)\) = 0.25 m
The charge on the larger drop,
Q = nq = 125 x (0.5 x 10—6)C
The electric potential of the surface of the larger drop,
V = \(\frac{1}{4πε_0}\frac{Q}{R}\) = (9 x 109) x \(\frac{125(0.5×10^{-6})}{0.25}\)
= 9 x 125 x 2 x 103 = 2.25 x 106 V
(10) The dipole moment of a water molecule is 6.3 × 10–30 Cm. A sample of water contains 1021 molecules, whose dipole moments are all oriented in an electric field of strength 2.5 × 105 N /C. Calculate the work to be done to rotate the dipoles from their initial orientation θ1 = 0 to one in which all the dipoles are perpendicular to the field, θ2 = 90°.
Given : p = 6.3 x 10–30 C-m, N = 1021 molecules, E=2.5 x 105 N/C,
θ0 = θ1 = 0°, θ = θ2 = 90°
W= pE(cos θ0 — cos θ)
The total work required to orient N dipoles is
W = NpE(cos θ1 — cos θ2)
= (1021)(6.3 x 10–30)(2.5 x 105)
= 15.75 x 10–4 J = 1.575 mJ
(11) A charge 6 μC is placed at the origin and another charge –5 μC is placed on the y axis at a position A (0, 6.0) m.
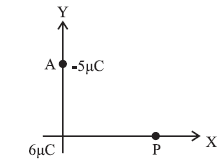
(a) Calculate the total electric potential at the point P whose coordinates are (8.0, 0) m
(b) Calculate the work done to bring a proton from infinity to the point P ? What is the significance of the negative sign ?
Given : q1 = 6 x 10−6 C, q2 = −5 x 10−6 C, A = (0, 6.0 m), P = (8.0m, 0),
r1 = OP = 8 m, q = e = 1.6 x 10−19 C, 1/4πε0 = 9 x 109 N-m2/C2
r2 = AP = \(\sqrt{(8-0)^2+(0-6)^2}\) = \(\sqrt{64+36}\) = 10 m
(a) The net electric potential at P due to the system of two charges is
V = V1 + V2 = \(\frac{1}{4πε_0}[\frac{q_1}{r_1}+\frac{q_2}{r_2}]\)
= (9 x 109)\([\frac{6×10^{-6}}{8}+\frac{-5×10^{-6}}{10}]\)
= (9 x 103)(0.75 − 0.5) = 2.25 x 103 V
= 2.25 kV
(b) The electric potential V at the point P is the negative of the work done per unit charge, by the electric field of the system of the charges q1 and q2, in bringing a test charge from infinity to that point.
V = −W/q0
∴ W = −qV = −(1.6 x 10−19)(2.25 x 103)
= −3.6 x 10−16 J = −2.25 keV
That is, in bringing the positively charged proton from a point of lower potential to a point of higher potential, the work done by the electric field on it is negative, which means that an external agent must bring the proton against the electric field of the system of the two source charges.
(12) In a parallel plate capacitor with air between the plates, each plate has an area of 6 × 10–3 m2 and the separation between the plates is 2 mm.
(a) Calculate the capacitance of the capacitor,
(b) If this capacitor is connected to 100 V supply, what would be the charge on each plate?
(c) How would charge on the plates be affected if a 2 mm thick mica sheet of k = 6 is inserted between the plates while the voltage supply remains connected ?
Given : k =1 (air), A = 6 × 10–3 m2, d = 2 mm = 2 × 10–3 m, V = 100 V,
t = 2 mm =d, k1 = 6, ε0 = 8.85 x 10–12 F/m
(a) The capacitance of the air capacitor,
C0 = \(\frac{ε_0A}{d}\) = \(\frac{(8.85×10^{-12})(6×10^{-3})}{2×10^{-3}}\)
= 26.55 x 10–12 F = 26.55 pF
(b) Q0 = C0V = (26.55 x 10–12)(100)
= 26.55 x 10–10 C = 2.655 nC
(c) The dielectric of relative permittivity k1 completely fills the space between the plates (‘.’ t = d), so that the new capacitance is C =k1C0.
With the supply still connected, V remains the same.
∴ Q = CV = kC0V = kQ0 = 6(2.655 nF) = 15.93 nC
Therefore, the charge on the plates increases.
[Note : C = k1C0= 6 (26.55 pF) = 159.3 pF.]
(13) Find the equivalent capacitance between P and Q. Given, area of each plate = A and separation between plates = d.
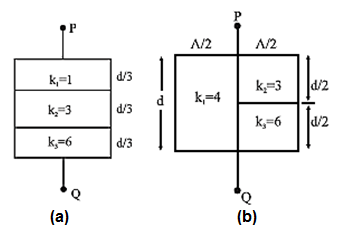
(i) The capacitor in Fig. (a) is a series combination of three capacitors of plate separations d/3 and plate areas A, with C1 filled with air (k1 = 1), C2 filled with dielectric of k2 =3 and C3 filled with dielectric of k3 = 6.
∴ C1 = \(\frac{k_1ε_0A}{d/3}=\frac{3ε_0A}{d}k_1\), C2 = \(\frac{k_2ε_0A}{d/3}=\frac{3ε_0A}{d}k_2\), C3 = \(\frac{k_3ε_0A}{d/3}=\frac{3ε_0A}{d}k_3\)
∴ \(\frac{1}{C'}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}\) = \(\frac{d}{3ε_0A}(\frac{1}{k_1}+\frac{1}{k_2}+\frac{1}{k_3})\)
∴ C’ = \(\frac{d}{3ε_0A}(\frac{k_1k_2k_3}{k_1k_2+k_2k_3+k_3k_1})\) = \(\frac{d}{3ε_0A}(\frac{18}{27}\)
= \(\frac{2ε_0A}{d}\)
(ii) In Fig. (b), a series combination of two capacitors C2(k2 =3) and C3 (k3 =6), of plate areas A/2 and plate separations d/2, is in parallel with a capacitor C1 (k1 =4) of plate area A/2 and plate separation d.
∴ C1 = \(\frac{k_1ε_0(A/2)}{d}=\frac{ε_0A}{2d}k_1\), C2 = \(\frac{k_2ε_0(A/2)}{d/2}=\frac{ε_0A}{d}k_2\), C3 = \(\frac{k_3ε_0(A/2)}{d/2}=\frac{ε_0A}{d}k_3\)
For the series combination of C2 and C3,
\(\frac{1}{C_4}=\frac{1}{C_2}+\frac{1}{C_3}\)
∴ C4 = \(\frac{C_2C_3}{C_2+C_3} = \frac{ε_0A}{d}(\frac{k_2k_3}{k_2+k_3})\)
= \(\frac{ε_0A}{d}(\frac{3×6}{3+6})\) = \(\frac{2ε_0A}{d}\)
Finally, for the parallel combination of C1 and C4,
C” = C1 + C4 = \(\frac{ε_0A}{2d}(4)+\frac{2ε_0A}{d}\) = \(\frac{4ε_0A}{d}\)
Thus, the equivalent capacitances are C’ = \(\frac{2ε_0A}{d}\) and C” = \(\frac{4ε_0A}{d}\).
Main Page : – Maharashtra Board Class 12th-Physics – All chapters notes, solutions, videos, test, pdf. Previous Chapter : Chapter-7-Wave Optics –Online Solution Next Chapter : Chapter-9-Current Electricity – Online Solution
We reply to valid query.