Solutions
Question 1. Choose the most correct option.
(i) The rate law for the reaction aA + bB → P is rate = k[A] [B]. The rate of reaction doubles if
(a) concentrations of A and B are both doubled.
(b) [A] is doubled and [B] is kept constant
(c) [B] is doubled and [A] is halved
(d) [A] is kept constant and [B] is halved.
Answer :
(b) [A] is doubled and [B] is kept constant
(ii) The order of the reaction for which the units of rate constant are mol dm−3 s−1 is …..
(a) 1
(b) 3
(c) 0
(d) 2
Answer :
(c) 0
(iii) The rate constant for the reaction 2 N2O5(g) → 2N2O4(g) + O2(g) is 4.98 × 10−4 s−1. The order of reaction is
(a) 2
(b) 1
(c) 0
(d) 3
Answer :
(b) 1
(iv) Time required for 90 % completion of a certain first order reaction is t. The time required for 99.9 % completion will be
(a) t
(b) 2t
(c) t/2
(d) 3t
Answer :
(d) 3t
(v) Slope of the graph ln[A]t versus t for first order reaction is
(a) −k
(b) k
(c) \(\frac{k}{2.303}\)
(d) \(-\frac{k}{2.303}\)
Answer :
(a) −k
(vi) What is the half life of a first order reaction if time required to decrease concentration of reactant from 0.8 M to 0.2 M is 12 h?
(a) 12 h
(b) 3 h
(c) 1.5 h
(d) 6 h
Answer :
(d) 6 h
(vii) The reaction, 3ClO− → ClO3− + 2Cl− occurs in two steps,
(i) 2 ClO− → ClO2−
(ii) ClO2− + ClO− → ClO3− + Cl−
The reaction intermediate is
(a) Cl−
(b) ClO2−
(c) ClO3−
(d) ClO−
Answer :
(b) ClO2−
(viii) The elementary reaction O3(g) + O(g) → 2O2(g) is
(a) unimolecular and second order
(b) bimolecular and first order
(c) bimolecular and second order
(d) unimolecular and first order
Answer :
(c) bimolecular and second order
(ix) Rate law for the reaction, 2NO + Cl2 → 2NOCl is rate = k[NO2]2[Cl2]. Thus of k would increase with
(a) increase of temperature
(b) increase of concentration of NO
(c) increase of concentration of Cl2
(d) increase of concentrations of both Cl2 and NO
Answer :
(a) increase of temperature
(x) For an endothermic reaction, X Y. If Ef is activation energy of the forward reaction and Er that for reverse reaction, which of the following is correct?
(a) Ef = Er
(b) Ef < Er
(c) Ef > Er
(d) ΔH = Ef − Er is negative
Answer :
(c) Ef > Er
Question 2. Answer the following in one or two sentences.
(i) For the reaction, N2(g) + 3H2(g) → 2NH3(g), what is the relationship among \(\frac{d[N_2]}{dt}\), \(\frac{d[H_2]}{dt}\) and \(\frac{d[NH_3]}{dt}\) ?
Answer :
N2(g) + 3H2(g) → 2NH3(g),
From the above reaction, when 1 mole of N2 reacts, 3 moles of H2 are consumed and 2 moles of NH3 are formed.
If the instantaneous rate R of the reaction is represented in terms of rate of the consumption of N2 then, R = \(-\frac{d[N_2]}{dt}\)
∴ Rate of consumption of H2 = \(-\frac{d[H_2]}{dt}\) = 3\(-\frac{d[N_2]}{dt}\) = 3R
∴ R = \(-\frac{d[N_2]}{dt}\) = \(-\frac{1}{3}\frac{d[H_2]}{dt}\)
Rate of formation of NH3 = \(+\frac{d[NH_3]}{dt}\) = \(2(-\frac{d[N_2]}{dt}\) = 2R
∴ R = \(-\frac{d[N_2]}{dt}\) = \(+\frac{1}{2}(\frac{d[NH_3]}{dt})\)
Hence the rate of reaction in terms of concentration changes in N2, H2 and NH3 may be represented as,
Rate (R) = \(-\frac{d[N_2]}{dt}\) = \(-\frac{1}{3}\frac{d[H_2]}{dt}\) = \(+\frac{1}{2}\frac{d[NH_3]}{dt}\)
(ii) For the reaction,
CH3Br(aq) + OH−(aq)
CH3OH (aq) +Br (aq), rate law is rate = k[CH3Br][OH ]
(a) How does reaction rate changes if [OH ] is decreased by a factor of 5 ?
(b) What is change in rate if concentrations of both reactants are doubled?
Answer :
Given :
(a) Rate = R = k[CH3Br] × [OH−]
If R1 and R2 are initial and final rates of reaction then,
R1 = k[CH3Br] x [OH−]1
R2 = k[CH3Br] x [OH−]2 = k [CH3Br] x \(\frac{1}{5}\) x [OH−]1
∴ \(\frac{R_2}{R_1}\) = \(\frac{k[CH_3BR]×\frac{1}{5}×[OH^-]_1}{k[CH_3BR]×[OH^-]_1}\) = \(\frac{1}{5}\)
∴ R2 = \(\frac{1}{5}\)R1
(b) R1 = k[CH3Br] x [OH−]
R2 = k × 2 × [CH3Br] × 2 x [OH−]
∴ \(\frac{R_2}{R_1}\) = \(\frac{k×2×[CH_3BR]×2×[OH^-]}{k×[CH_3BR]×[OH^-]}\) = 4
∴ R2 = 4R1
Rate will be increased 4 time.
(iii) What is the relationship between coefficients of reactants in a balanced equation for an overall reaction and exponents in rate law. In what case the coefficients are the exponents?
Answer :
Consider the following reaction,
aA + bB → products
If the rate of the reaction depends on the concentrations of the reactants A and B, then, by rate law,
R ∝ [A]a [B]b
∴ R = k [A]a [B]b
where [A] = concentration of A and [B] = concentration of B
The proportionality constant k is called the velocity constant, rate constant or specific rate of the reaction.
‘a’ and ‘b’ are the exponents or the powers of the concentrations of the reactants A and B respectively when observed experimentally.
The exponents or powers may not be necessarily a and b but may be different x and y depending on experimental observations. Then the rate R will be,
R = k [A]x × [B]y
For example, if x = 1 and y = 2, then,
R = k [A] × [B]2
(iv) Why all collisions between reactant molecules do not lead to a chemical reaction?
Answer :
All collisions of reactant molecules do not lead to a chemical reaction because the colliding molecules need to possess certain energy which is greater than the activation energy Ea of the molecule needed for the reaction to occur and proper orientation of molecules is needed for the reaction to occur.
(v) What is the activation energy of a reaction?
Answer :
For the reaction to occur the colliding reactant molecules must possess the minimum kinetic energy. This minimum kinetic energy is the activation energy.
(vi) What are the units for rate constants for zero order and second order reactions if time is expressed in seconds and concentration of reactants in mol/L?
Answer :
For a zero order reaction, the rate constant has units,
mol L−1s−1.
For second order reaction,
Rate = k x [Reactant]2
∴ k = \(\frac{Rate [mol L^{-1}s^{-1}}]{Reactant^2[mol L^{-1}]^2}\) = mol−1L s−1
Units of k are mol−1L s−1
(vii) Write Arrhenius equation and explain the terms involved in it.
Answer :
Arrhenius equation is represented as
k = A X e−Ea/RT
where
k = Rate constant at absolute temperature T
Ea = Energy of activation
R = Gas constant
A = Frequency factor or pre−exponential factor.
(viii) What is the rate determining step?
Answer :
- Many chemical reactions take place in a series of elementary steps.
- Among many steps of the reaction, one of the steps is the slowest step compared to other steps.
- The slowest step in the reaction mechanism which involves many steps is called rate determining step.
(ix) Write the relationships between rate constant and half life of first order and zeroth order reactions.
Answer :
(A) For the first order reaction, half life, t1/2 is given by, t1/2 = \(\frac{0.693}{k}\)
where k is rate constant.
(B) Zero order reaction, , t1/2 = \(\frac{[A]_0}{2k}\)
where k is the rate constant and [A]o is initial concentration of the reactant.
(x) How do half lives of the first order and zero order reactions change with initial concentration of reactants?
Answer :
(A) For the first order reaction, half life, t1/2 is given by, t1/2 = \(\frac{0.693}{k}\)
where k is rate constant. Hence it is independent of initial concentration of the reactant.
(B) Zero order reaction, , t1/2 = \(\frac{[A]_0}{2k}\)
where [A]o is initial concentration of the reactant. Hence, half life period increases with the increase in concentration of the reactant.
Question 3. Answer the following in brief.
(i) How instantaneous rate of reaction is determined?
Answer :
(1) The instantaneous rate is expressed as an infinitesimal change in concentration (−dc) of the reactant with the infinitesimal change in time (dt).
For a reaction, A → B let an infinitesimal change in A be −dc in time dt, then
Rate = \(\frac{d[A]}{dt}\)
Hence, it is represented as,
∴ Instantaneous rate = \(\frac{-d[A]}{dt}\)
Negative sign indicates decrease in the concentration of A.
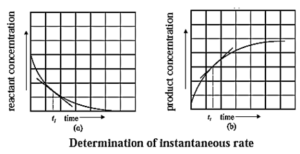
It is obtained by drawing a tangent to the curve obtained by plotting the concentration against the time. Hence, the slope at a given point represents the instantaneous rate of the reaction.
(2) The instantaneous rate can also be expressed as an infinitesimal change (or increase) in the concentration of the product with the infinitesimal change in time (dt).
Let dB be an infinitesimal change in the concentration of product B in time dt, then
Rate = \(\frac{d[B]}{dt}\) = \(\frac{dx}{dt}\)
Hence,
Instantaneous rate = \(\frac{dx}{dt}\)
It is obtained from the slope of the curve obtained by plotting the concentration of the product against time.
The instantaneous rate is more useful in obtaining the rate law integrated equations.
(ii) Distinguish between order and molecularity of a reaction.
Answer :
| order | molecularity |
| It is sum of the concentration terms on which the rate of reaction actually depends or it is the sum of the exponents of the concentrations in the rate law equation. | It is the number of molecules (or atoms or ions) of the reactants taking part in the elementary reaction. |
| It need not be a whole number i.e. it can be fractional as well as zero. | It is always an whole number. |
| It can be determined experimentally only and cannot be calculated. | It is theoretical property and indicates the number of molecules of reactant in
each step of the reaction. |
| Its value depends upon experimental conditions. | Its value does not depend upon experimental conditions. |
| It is the property of elementary and complex reactions. | It is the property of elementary reactions only. |
| Rate law expression describes the order of the reaction. | Rate law does not describe molecularity. |
(iii) A reaction takes place in two steps,
(1) NO(g) + Cl2(g) → NOCl2(g)
(2) NOCl2(g) + NO(g) → 2NOCl(g)
(a) Write the overall reaction.
(b) Identify reaction intermediate.
(c) What is the molecularity of each step?
Answer :
Given :
(1) NO(g) + Cl2(g) → NOCl2(g)
(2) NOCl2(g) + NO(g) → 2NOCl(g)
(a) Overall reaction is obtained by adding both the reactions
2NO(g) + Cl2(g) → 2NOCl2(g)
(b) The reaction intermediate is NOCl2, since it is formed in first step and consumed in the second step.
(c) Since the first step is a slow and rate determining step, the molecularity is two.
Since the second step is a fast step its molecularity is not considered.
(iv) Obtain the relationship between the rate constant and half life of a first order reaction.
Answer :
Consider the following reaction,
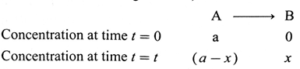
If [A]0 and [A]t are the concentrations of A at start and after time t, then [A]0 = a and [A]t = a − x.
The velocity constant or the specific rate constant k for the first order reaction can be represented as,
k = \(\frac{2.303}{t}log_{10}\frac{[A]_0}{[A]_t}\)
∴ k = \(\frac{2.303}{t}log_{10}\frac{a}{(a-x)}\)
where, a is the initial concentration of the reactant A, x is the concentration of the product B after time
t, so that (a − x) is the concentration of the reactant
A after time t.
Half−life of a reaction : The time required to reduce the concentration of the reactant to half of its initial value is called the half−life period or the half−life of the reaction.
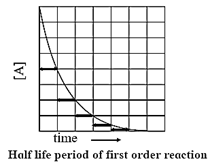
If t1/2 is the half−life of a reaction, then at t = t1/2,
X = a/2, hence a — x = a — a/2 = a/2
Now,
k = \(\frac{2.303}{t}log_{10}\frac{a}{(a-x)}\)
∴ t = \(\frac{2.303}{k}log_{10}\frac{a}{(a-x)}\)
Hence,
t1/2 = \(\frac{2.303}{k}log_{10}\frac{a}{(a-a/2)}\) = \(\frac{2.303}{k}log_{10}\frac{a}{(a/2)}\)
= \(\frac{2.303}{k}log_{10}2\) = \(\frac{2.303×0.3010}{k}\)
∴ t1/2 = 0.693/k
Hence, for a first order reaction, the half-life of the reaction is independent of the initial concentration of the reactant.
(v) How will you represent zeroth order reaction graphically?
Answer :
(a) A graph of concentration against time : In case of a zero order reaction, the rate of reaction is independent of the concentration of the reactant.
The concentration [A]t of the reactant at a time t is given by
[A]t = −kt + [A]0 …(y = −m + c)
where [A]0 is the initial concentration of the reactant and k is a rate constant.
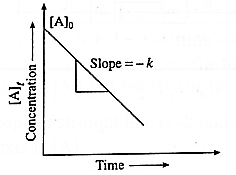
Hence in case of zero order reaction, when the concentration of the reactant is plotted against time, a straight line with the slope equal to −k is obtained. The concentration of the reactants decrease with time. The intercept on the concentration axis gives the initial concentration, [A]0.
A graph of rate of a reaction against the concentration of the reactant :
Rate of a Zero Order reaction is independent of the concentration of the reactant.
Rate, R = k [A]0 = k
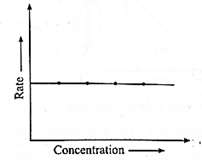
Hence even if the concentration of the reactant decreases, the rate of the reaction remains constant.
Therefore if the rate of a zero order reaction is plotted against concentration, then a straight line with zero slope is obtained indicating, no change in the rate of the reaction with a change in the concentration of the reactants.
A graph of half-life period against concentration :
The half-life period of a zero order reaction is given by, t1/2 = (\frac{[A]_0{2k}\) where [A]0 is initial concentration of the reactant and k is the rate constant. Hence the half-life period is directly proportional to the concentration.
When a graph of t1/2 is plotted against concentration, a straight line passing through origin is obtained, and the slope gives \(\frac{1}{2k}\), where k is the rate constant.
(vi) What are pseudo−first order reactions? Give one example and explain why it is pseudo−first order.
Answer :
Pseudo first order reaction :
A reaction which has higher order true rate law but experimentally found to behave as first order is called pseudo first order reaction.
Explanation : Consider an acid hydrolysis reaction of an ester like methyl acetate.
CH3COOCH3(aq) + H2O(l) \(\underrightarrow{H^+_{(aq)}}\) CH3C00H(aq) + CH3OH(aq)
Since the reaction involves two substances, ester and water, it is a bimolecular reaction and the true rate law should be,
Rate = k’ [CH3COOCH3] x [H2O]
Hence the reaction is expected to follow second order kinetics. However experimentally it is found that the reaction follows first order kinetics.
This is because solvent water being in a large excess, its concentration remains constant. Hence, [H2O] = constant = k”
Rate = k’ [CH3COOCH3] x [H2O]
= k’ [CH3COOCH3] x k”
= k’ x k” x [CH3COOCH3]
If k’ x k” = k, then Rate = k [CH3COOCH3].
This indicates that second order true rate law is forced into first order rate law. Therefore this bimolecular reaction which appears of second order is called pseudo first order reaction.
(vii) What are requirements for the colliding reactant molecules to lead to products?
Answer :
(a) Collision between reactant molecules :
- In order for a reaction to happen, the reacting species (atoms, ions, or molecules) must come into contact with one another and collide. As a result, the rate of the reaction will depend on the frequency and rate of collisions, which rise with temperature and the number of reacting species.
- As opposed to the rate of collisions between reacting species in gaseous or liquid phases, it is seen that the rate of reaction is extremely low. This implies that not every collision will result in a reaction. As a result, in addition to collision frequency, another factor like the energy of the interacting species must be taken into account.
(b) Activation :
- For the reaction to occur the colliding reactant molecules must possess the minimum kinetic energy. This minimum kinetic energy is the activation energy. The reaction would occur only if colliding molecules possess kinetic energies equal to or greater than the activation energy.
(c) Orientation of reactant molecules :
The concept of activation energy is satisfactory in case of simple molecules or ions but not in case of complex or higher polyatomic molecules. It is observed that the rates of reaction are less as compared to the rates of collisions between activated molecules with activation energy.
This suggests that in addition, the colliding molecules must have proper orientations relative to each other during collisions.
For example, consider the reaction,
A — B + C → A + B — C.
For the reaction to occur, C must collide with B while collisions with A will not be fruitful. Since B has to bond with C.
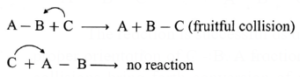
(viii) How catalyst increases the rate of reaction? Explain with the help of potential energy diagram for catalyzed and uncatalyzed reactions.
Answer :
Effect of a catalyst on the rate of reaction :
A catalyst is a substance, when added to the reactants, increases the rate of the reaction without being consumed.
For example, the decomposition of KClO3 in the presence of small amount of MnO2 is very fast but very slow in the absence of MnO2.
2KClO3(s) \(\underrightarrow{MnO_2+Δ}\) 2KCl(s) + 3O2(g)
- The phenomenon of catalysed reaction is called catalysis and depends on nature of the catalyst. In heterogeneous catalysis, the reactant molecules are adsorbed on the solid catalyst surface while in case of homogeneous catalysis, the catalyst reacts with one of the reactants, forms intermediate and decomposes reforming original catalyst and the products.
- The catalyst provides alternative and lower energy path or mechanism for the reaction.
- In the presence of the catalyst, the activation energy of the reaction is lowered. The height of activation energy barrier is less than that in the uncatalysed reaction.
- Due to lowering of energy of activation, (Ea) the number of molecules possessing Ea increases, hence the rate of the reaction increases.
- The rate constant = k = A x e−Ea/RT where A is a frequency factor and hence the rates of the catalyzed reaction are higher than those of uncatalysed reactions.
- The catalyst does not change the extent of the reaction but hastens the reaction.
- The catalyst enters the reaction but does not appear in the balanced equation since it is consumed in one step and regenerated in another.
(ix) Explain with the help of Arrhenius equation, how does the rate of reaction changes with (a) temperature and (b) activation energy.
Answer :
(a) By Arrhenius equation,
Rate constant = k = A x e−Ea/RT
where k is rate constant, A is a frequency factor and Ea is energy of activation at temperature T. As Ea increases, the rate constant and rate of the reaction decreases.
(b) As temperature increases Ea/RT decreases but due to negative sign, k and rate increase with the increase in temperature.
(x) Derive the integrated rate law for first order reaction.
Answer :
Consider the following first order reaction, A → B
The rate of the chemical reaction is given by the rate law expression as,
Rate, R = k [A]
where [A] is the concentration of the reactant A and k is the velocity constant or specific rate of the reaction.
The instantaneous rate is given by,
R = k [A] = \(\frac{-d[A]}{dt}\)
∴ \(\frac{-d[A]}{[A]}\) = k.dt
If [A]0 is the initial concentration of the reactant and [A]t at time t, then by integrating the above equation,
\(\int_{[A]_0}^{[A]_t}\frac{d[A]}{[A]}\) =\(k\int_{0}^{t}dt\)
∴ \(-log_e\frac{[A]_t}{[A]_0}\) = kt …(1)
∴ \(log_e\frac{[A]_0}{[A]_t}\) = kt
∴ k = \(\frac{1}{t}log_e\frac{[A]_0}{[A]_t}\)
∴ k = \(\frac{2.303}{t}log_{10}\frac{[A]_0}{[A]_t}\) ….(2)
This is the integrated rate equation for the first order reaction. This is also called integrated rate law.
(xi) How will you represent first order reactions graphically.
Answer :
(i) A graph of rate of a reaction and concentration :
The differential rate law for first order reaction, A → Products is represented as,
Rate = \(\frac{-d[A]}{dt}\) = k[A]
Rate = k x [A], (y = mx). When the rate of a first order reaction is plotted against concentration, [A]t, a straight line graph is obtained.
With the increase in the concentration [A]t, rate R, increases. The slope of the line gives the value of rate constant k.
(ii) A graph of concentration against time : When the concentration of the reactant is plotted against time t, a curve is obtained. The concentration [A]t, of the reactant decreases exponentially with time. The variation in the concentration can be represented as,
[A]t = [A]0e−kt
where [A]0 and [A]t are initial and final concentrations the reactant and k is the rate constant. The time required to complete the first order reaction is infinity.
(iii) A graph of log10(a — x) against time t :
k = \(\frac{2.303}{t}log_{10}\frac{a}{(a-x)}\)
∴ k = \(\frac{2.303}{t}[log_{10}a-log_{10}(a-x)]\)
∴ \(\frac{kt}{2.303}\) = \(log_{10}a-log_{10}(a-x)\)
∴ log10(a − x) = \(-\frac{kt}{2.303}\) + log10 a ……(y = −mx + c)
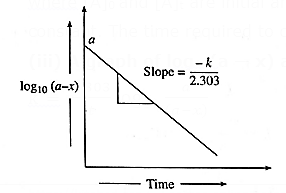
When log10(a — x) is plotted against time t, a straight line with negative slope is obtained, from which the velocity constant k can be calculated.
A graph of half-life period and concentration :
The half-life period, t1/2 of a first order reaction is given by t1/2 = 0.693/k, Where k is the rate constant.
For the given reaction at constant temperature, t1/2 is constant and independent of the concentration of the reactant.
Hence when a graph of t1/2 is plotted against concentration, a straight line parallel to the concentration axis (slope = zero) is obtained.
A graph of \(log_{10}\frac{a}{(a-x)}\) against time :
The rate constant, for a first order reaction is represented as,
k = \(\frac{2.303}{t}log_{10}\frac{a}{(a-x)}\) = \(\frac{2.303}{t}log_{10}\frac{[A]_0}{[A]_t}\)
where [A]0 and [A]t, are the respective initial and final concentrations of the reactant after time t.
∴ \(log_{10}\frac{a}{(a-x)}\) = \(\frac{k}{2.303}×t\) ….(y = mx)
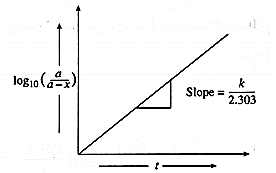
When \(log_{10}(\frac{a}{a-x})\) is plotted against time t, a straight line graph passing through the origin is obtained and the slope gives the value of k/2.303.
From this slope, the rate constant can be calculated.
(xii) Derive the integrated rate law for the first order reaction, A(g) → B(g) + C(g) in terms of pressure.
Answer :
Integrated rate law for gas phase f reactions :
For the gas phase reaction,
A(g) → B(g) + C(g)
Let initial pressure of A be Pi that decreases by x within time t.
Pressure of reactant A at time t
PA = Pi – x ….(1)
The pressures of the products B and C at time t are
PB = PC = x
The total pressure at time t is then
P = Pi – x + x + x = Pi + x
Hence, x = P – Pi …….(2)
Pressure of A at time t is obtained by substitution of Eq. (2) into Eq. (1). Thus
PA = Pi – (P – Pi) = Pi – P + Pi = 2Pi – P
The integrated rate law turns out to be
k = \(\frac{2.303}{t}log_{10}\frac{[A]_0}{[A]_t}\)
The concentration now expressed in terms of pressures.
Thus, [A]0 = Pi and [A]t = PA = 2Pi – P
Substitution gives in above
∴ k = \(\frac{2.303}{t}log_{10}\frac{P_i}{2P_i-P}\)
P is the total pressure of the reaction mixture at time t
(xiii) What is zeroth order reaction? Derive its integrated rate law. What are the units of rate constant?
Answer :
Zero order reaction : A reaction in which the rate of the reaction does not depend on the concentration of any reactant taking part in the reaction is called zero order reaction.
Expression for Integrated rate law for zero order reactions :
Consider a zero order reaction, A → Products
The rate of the reaction is,
Rate = \(\frac{-d[A]}{dt}\)
By rate law,
Rate = k x [A]0 = k
∴ −d[A] = k x dt
If [A]0 is the initial concentration of the reactant A at t = 0 and [A]t is the concentration of A present after time t, then by integrating above equation,
\(\int_{[A]_0}^{[A]_t} -d[A] = \int_{t=0}^{t=t}k \,dt\)
\(-\int_{[A]_0}^{[A]_t} d[A] = k\int_{t=0}^{t=t}dt\)
\([A]_{[A]_0}^{[A]_t} = k[t]_o^t\)
− ( [A]t − [A]0 ) = kt
∴ [A]0 − [A]t = kt
∴ k = \(\frac{[A]_0-[A]_t}{t}\)
This is the integrated rate law expression for rate constant for zero order reaction.
∴ k x t= [A]0 − [A]t
[A]t = −kt + [A]0
Units of rate constant of zero order reactions :
k = \(\frac{[A]_0-[A]_t}{t}=\frac{mol\,L^{-1}}{s}\) = mol L−1 s−1
The units of rate constant of zero order reaction are the same as the rate.
(xiv) How will you determine activation energy: (a) graphically using Arrhenius equation (b) from rate constants at two different temperatures?
Answer :
(a) Graphical determination of activation energy :
ln k = ln A − \(\frac{E_a}{RT}\)
2.303 log10 k = 2.303 log10 A − \(\frac{E_a}{RT}\)
∴ log10 k = log10 A − \(\frac{E_a}{2.303RT}\)
∴ log10 k = − \((\frac{E_a}{RT})×\frac{1}{T}\) + log10 A …( y = −mx + c)
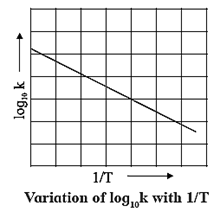
When log10 k is plotted against 1/T a straight line with negative slope is obtained. From the slope of the graph, energy of activation Ea, is obtained as follows :
Slope = \(\frac{E_a}{2.303R}\)
∴ Ea = 2.303 R x Slope
(b) For the given reaction, rate constants k1 and k2 are measured at two different temperatures T1 and T2 respectively. Then,
log10\(\frac{k_2}{k_1}\) = \(\frac{E_a(T_2-T_1)}{2.303RT_1T_2}\)
where Ea is the energy of activation.
Hence by substituting appropriate values of k1 and k2, energy of activation Ea for the reaction is determined.
(xv) Explain graphically the effect of temperature on the rate of reaction.
Answer :
Graphical description of effect of temperature :
- It has been observed that the rates of chemical reactions increase as temperature increases.
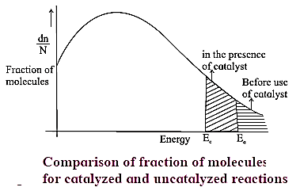
- As the temperature increases, the kinetic energy of the molecules increases as well. The fraction of molecules with the lowest energy barrier, i.e. activation energy Ea, increases as temperature rises.
- As a result, the fraction of colliding molecules with kinetic energy (Ea) increases, and the rate of the reaction increases as temperature increases.
- The figure below shows that the area representing the fraction of molecules with kinetic energy greater than Ea is larger at higher temperatures T2 than at lower temperatures T1. This explains why the rate of the reaction increases as temperature rises.
- The shaded area to the right of activation energy Ea represents fraction of collisions of activated molecules having energy Ea or greater.
(xvi) Explain graphically the effect of catalyst on the rate of reaction.
Answer :
Effect of a catalyst on the rate of reaction :
- The phenomenon of catalysed reaction is called catalysis and depends on nature of the catalyst. In heterogeneous catalysis, the reactant molecules are adsorbed on the solid catalyst surface while in case of homogeneous catalysis, the catalyst reacts with one of the reactants, forms intermediate and decomposes reforming original catalyst and the products.
- The catalyst provides alternative and lower energy path or mechanism for the reaction.
- In the presence of the catalyst, the activation energy of the reaction is lowered. The height of activation energy barrier is less than that in the uncatalysed reaction.
- Due to lowering of energy of activation, (Ea) the number of molecules possessing Ea increases, hence the rate of the reaction increases.
- The rate constant = k = A x e−Ea/RT where A is a frequency factor and hence the rates of the catalyzed reaction are higher than those of uncatalysed reactions.
- The catalyst does not change the extent of the reaction but hastens the reaction.
- The catalyst enters the reaction but does not appear in the balanced equation since it is consumed in one step and regenerated in another.
(xvii) For the reaction 2A + B → products, find the rate law from the following data.
| [A]/M | [B]/M | rate/M s−1 |
| 0.3 | 0.05 | 0.15 |
| 0.6 | 0.05 | 0.3 |
| 0.6 | 0.2 | 1.2 |
Answer :
Given : 2A + B → Products
Rates : R1 = 0.15 M s−1, R2 = 0.3 M s−1
[A]1 = 0.3 M, [A]2 = 0.6 M
[B]1 = 0.05 M, [B]2 = 0.05 M
(i) If order of the reaction in A is x and in B is y then, by rate law,
Rate = R1 = k[A]1x [B]1y and R2 = k[A]2x [B]2y
∴ \(\frac{R_2}{R_1}\) = \(\frac{k[A]^x_2[B]^y_2}{k[A]^x_1[B]^y_1}\)
∴ = \((\frac{[A]_2}{[A]_1})^x×(\frac{[B]_2}{[B]_1})^y\)
∴ \(\frac{0.3}{0.15}\) = \((\frac{0.6}{0.3})^x×(\frac{0.05}{0.05})^y\)
2 = 2x
∴ x = 1. Hence, the reaction has order one in A.
Rates : R1 = 0.3 M s−1, R2 = 1.2 M s−1
[A]1 = 0.6 M, [A]2 = 0.6 M
[B]1 = 0.05 M, [B]2 = 0.2 M
(i) If order of the reaction in A is x and in B is y then, by rate law,
Rate = R1 = k[A]1x [B]1y and R2 = k[A]2x [B]2y
∴ \(\frac{R_2}{R_1}\) = \(\frac{k[A]^x_2[B]^y_2}{k[A]^x_1[B]^y_1}\)
∴ = \((\frac{[A]_2}{[A]_1})^x×(\frac{[B]_2}{[B]_1})^y\)
∴ \(\frac{1.2}{0.3}\) = \((\frac{0.6}{0.6})^x×(\frac{0.2}{0.05})^y\)
4 = 4y
∴ y = 1. Hence the reaction has order one in B.
The order of overall reaction = n = nA + nB = 1 + 1 = 2
Rate = R = k[A] × [B]
Answer is : Rate law : Rate = k [A] × [B];
Question 4. Solve
(i) In a first order reaction, the concentration of reactant decreases from 20 mmol dm−3 to 8 mmol dm−3 in 38 minutes. What is the half life of reaction?
Answer :
Given : [A]0 = 20 mmol dm−3; [A]t = 8 mmol dm−3; t = 38 min; t1/2 = ?
k = \(\frac{2.303}{t}log_{10}\frac{[A]_0}{[A]_t}\) = \(\frac{2.303}{38}log_{10}\frac{20}{8}\)
= \(\frac{2.303}{38}\) x 0.3979 = 0.02411 min−1
t1/2 = \(\frac{0.693}{k}\) = \(\frac{0.693}{0.02411}\) = 28.74 min
Answer is : Half period is 28.7 min.
(ii) The half life of a first order reaction is 1.7 hours. How long will it take for 20% of the reactant to react?
Answer :
Given : t1/2 = 1.7 hr; [A]0 = 100; [A]t = 100 − 20 = 80; t = ?
t1/2 = \(\frac{0.693}{k}\)
∴ k = \(\frac{0.693}{t_{1/2}}\) = \(\frac{0.693}{1.7}\) = 0.4076 hr−1
∴ k = \(\frac{2.303}{t}log_{10}\frac{[A]_0}{[A]_t}\) = \(\frac{2.303}{38}log_{10}\frac{20}{8}\)
∴ t = \(\frac{2.303}{k}log_{10}\frac{100}{80}\)
= \(\frac{2.303}{0.4076}\)log10 1.25 = \(\frac{2.303×0.9691}{0.4076}\)
= 0.5476 hr = 0.5476 × 60 min
= 32.9 min
Answer is : Time required = t = 32.9 min
(iii) The energy of activation for a first order reaction is 104 kJ/mol. The rate constant at 25 0C is 3.7 × 10−5 s−1. What is the rate constant at 300C? (R = 8.314 J/K mol)
Answer :
Given : E = 104 kJ mol−1 = 104 x 103 Jmol−1, k1 = 3.7 × 10−5 s−1;
T = 273 + 25 = 298K, T2 = 273 + 30 = 303 K; k2 = ?
log10 \(\frac{k_2}{k_1}\) = \(\frac{E_a×(T_2-T_1)}{2.303×R×T_1×T_2}\)
∴ log10 k2 − log10 k1 = \(\frac{E_a×(T_2-T_1)}{2.303×R×T_1×T_2}\)
∴ log10 k2 = log10 k1 + \(\frac{E_a×(T_2-T_1)}{2.303×R×T_1×T_2}\)
= log10 (3.7 × 10−5) + \(\frac{104×10^3(303-298)}{2.303×8.314×298×303}\)
= \(\bar{5}.5682 + 0.3\) = −4.4318 + 0.3 = − 4.1318
k2 = Antilog − 4.1318 = Antilog \(\bar{5}.5682\) = 7.382 × 10−5 s−1
Answer is : k2 = 7.382 × 10−5 s−1
(iv) What is the energy of activation of a reaction whose rate constant doubles when the temperature changes from 303 K to 313 K?
Answer :
Given : k2 = 2k1, T1 = 303 K; T2 = 313 K; Ea = ?
log10 \(\frac{k_2}{k_1}\) = \(\frac{E_a×(T_2-T_1)}{2.303×R×T_1×T_2}\)
∴ Ea = \(\frac{2.303×R×T_1×T_2}{T_2-T_1}\) × log10 \(\frac{k_2}{k_1}\)
= \(\frac{2.303×8.314×303×313}{313-303}\) × log10 \(\frac{2k_1}{k_1}\)
= \(\frac{2.303×8.314×303×313}{313-303}\ × 0.3010
= 54660 J = 54.66 kJ
Answer is : Energy of activation = E = 54.66 kJ.
(v) The rate constant of a reaction at 5000C is 1.6 × 103 M−1s−1. What is the frequency factor of the reaction if its activation energy is 56 kJ/mol.
Answer :
Given : k = 1.6 × 103 M−1s−1; T = 273 + 500 = 773 K
Energy of activation = E = 56 kJ mol−1 = 56000 J mol−1 , Frequency factor = A =?
By Arrhenius equation,
k = Axe−Ea/RT
∴ ln k = ln A − \(\frac{E_a}{RT}\)
2.303 log10 k = 2.303 log10 A − \(\frac{E_a}{RT}\)
∴ log10 k = log10 A − \(\frac{E_a}{2.303RT}\)
∴ log10 A = log10 k + \(\frac{E_a}{2.303RT}\) = log10(1.6 × 103) + \(\frac{56000}{2.303×8.314×773}\)
= 3.204 + 3.784 = 6.988
∴ A = Antilog 6.988 = 9.727 x 106 M−1s−1
Answer is : Frequency factor= A = 9.727 x 106 M−1s−1
(vi) Show that time required for 99.9% completion of a first order reaction is three times the time required for 90% completion.
Answer :
Given : For 99.9 % completion, if [A]0 = 100, [A]t = 100 − 99.9 = 0.1
For 90 % completion, if [A]0 = 100, [A]t = 100 – 90 = 10
k = \(\frac{2.303}{t}log_{10}\frac{[A]_0}{[A]_t}\)
∴ t = \(\frac{2.303}{k}log_{10}\frac{[A]_0}{[A]_t}\)
If t1 and t2 are the times required for 99.9 % and 90 % completion of reaction respectively, then
\(\frac{t_1}{t_2}\) = \(\frac{\frac{2.303}{k}log_{10}\frac{100}{0.1}}{\frac{2.303}{k}log_{10}\frac{100}{10}}\)
= \(\frac{log\,1000}{log\,10}\)
= log 103 = 3 log 10 = 3
∴ t1 = 3t2
∴ Time required for 99.9 % completion of a first order reaction is three time the time required for 90 % completion of the reaction.
(vii) A first order reaction takes 40 minutes for 30% decomposition. Calculate its half life.
Answer :
Given : [A]0 = 100 ; [A]t = 100 – 30 = 70; t = 40 min; t1/2 = ?
k = \(\frac{2.303}{t}log_{10}\frac{[A]_0}{[A]_t}\) = \(\frac{2.303}{40}log_{10}\frac{100}{70}\)
= \(\frac{2.303}{40}\)log10 1.4286 = \(\frac{2.303×0.1549}{40}\) = 8.918 x 10−3 min−1
t1/2 = \(\frac{0.693}{k}\) = \(\frac{0.693}{8.918×10^{-3}}\) = 77.70 min
Answer is : Half life period = 77.70 min.
(viii) The rate constant for the first order reaction is given by log10 k = 14.34 − 1.25 × 104/T. Calculate activation energy of the reaction.
Answer :
Given : log10 k = 14.34 – \(\frac{1.25×10^4}{T}\) ….(1)
From Arrhenius equation we can write,
log10 k = log10 A − \(\frac{E_a}{2.303RT}\) ….(2)
By comparing equations (1) and (2),
\(\frac{E_a}{2.303R}\) = 1.25 x 104
∴ Ea = 1.25 x 104 × 2.303 × R
= 1.25 x 104 × 2.303 × 8.314
= 23.93 × 104 J
= 239.3 kJ mol−1
Answer is : Energy of activation = Ea = 239.3 kJ mol−1
(ix) What fraction of molecules in a gas at 300 K collide with an energy equal to activation energy of 50 kJ/mol ?
Answer :
Given : T= 300 K; E2 = 50 kJ mol−1 = 50 × 103 Jmol−1
The fraction of molecules undergoing fruitful collisions is
f = \(e^{-E_a/RT}\) = \(e^{-50×10^3/8.314×300}\) = e−20.0465
∴ log10 f = \(\frac{-20.0465}{2.303}\) = − 8.7045
∴ f = Antilog − 8.7045
= Antilog \(\bar{9}.2955\) = 1.974 × 10−9
≈ 2 x 10−9
Answer is : Fraction of molecules undergoing collision = 2 x 10−9.
We reply to valid query.