Oscillations
Maharashtra Board-Class-12th-Physics-Chapter-5
Solution
Question 1.
Choose the correct option.
i) A particle performs linear S.H.M. starting from the mean position. Its amplitude is A and time period is T. At the instance when its speed is half the maximum speed, its displacement x is
(A) \(\frac{\sqrt{3}}{2}A\)
(B) \(\frac{2}{\sqrt{3}}A\)
(C) A/2
(D) A
(A) \(\frac{\sqrt{3}}{2}A\)
ii) A body of mass 1 kg is performing linear S.H.M. Its displacement x (cm) at t (second) is given by x = 6 sin (100t + p/4). Maximum kinetic energy of the body is
(A) 36 J
(B) 9 J
(C) 27 J
(D) 18 J
(D) 18 J
iii) The length of second's pendulum on the surface of earth is nearly 1 m. Its length on the surface of moon should be [Given: acceleration due to gravity (g) on moon is 1/6 th of that on the earth’s surface]
(A) 1/6 m
(B) 6 m
(C) 1/36 m
(D) \(\frac{1}{\sqrt{6}}m\)
(A) 1/6 m
iv) Two identical springs of constant k are connected, first in series and then in parallel. A metal block of mass m is suspended from their combination. The ratio of their frequencies of vertical oscillations will be in a ratio
(A) 1:4
(B) 1:2
(C) 2:1
(D) 4:1
(B) 1:2
v) The graph shows variation of displacement of a particle performing S.H.M. with time t. Which of the following statements is correct from the graph?
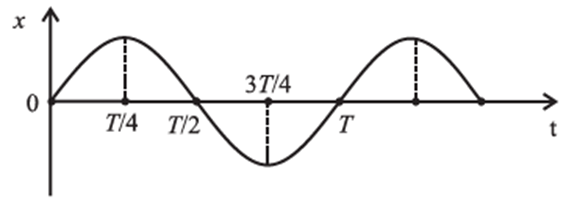
(A) The acceleration is maximum at time T.
(B) The force is maximum at time 3T/4.
(C) The velocity is zero at time T/2.
(D) The kinetic energy is equal to total energy at time T/4.
(B) The force is maximum at time 3T/4.
Question 2.
Answer in brief.
i) Define linear simple harmonic motion.
It is defined as the linear periodic motion of a body, in which the force (or acceleration) is always directed towards the mean position and its magnitude is proportional to the displacement from the mean position. OR A particle is said to execute linear SHM if the particle undergoes oscillations about a point of stable equilibrium, subject to a linear restoring force always directed towards that point and whose magnitude is proportional to the magnitude of the displacement of the particle from that point.
ii) Using differential equation of linear S.H.M, obtain the expression for (a) velocity in S.H.M., (b) acceleration in S.H.M.
The general expression for the displacement of a particle in SHM at time t is x = A sin(ωt + α) ….. (1) where A and ω is a constant in a particular case and α is the initial phase. The velocity of the particle is \(v=\frac{dx}{dt}=\frac{d}{dt}[A sin(ωt + α)]\) = ωA cos(ωt + α) = \(ωA\sqrt{1-sin^2(ωt + α)}\) From Eq. (1), sin(ωt + α) = x/A \(v=ωA\sqrt{1-\frac{x^2}{A^2}}\) ∴ \(v=ω\sqrt{A^2-x^2}\) …… (2) Equation (2) gives the velocity as a function of x The acceleration of the particle is a= \(\frac{dv}{dt}=\frac{d}{dt}\)[Aω cos(ωt + α)] ∴ a = − ω2A sin(ωt + α) But from Eq. (1), A sin(ωt + α) = x ∴ a = − ω2x ……. (3) Equation (3) gives the acceleration as a function of x. The minus sign shows that the direction of the acceleration is opposite to that of the displacement.
iii) Obtain the expression for the period of a simple pendulum performing S.H.M.
Consider a simple pendulum of length L, suspended from a rigid support O. When displaced from its initial position of rest through a small angle q in a vertical plane and released, it performs oscillations between two extremes, B and C, as shown in Fig. At B, the forces on the bob are its weight mg and the tension T’ in the string. Resolve mg into two components : mg cos θ in the direction opposite to that of the tension and mg sin θ perpendicular to the string. mg cos θ is balanced by the tension in the string. mg sin θ restores the bob to the equilibrium position. Restoring force, F = − mg sin θ If θ is small and expressed in radian, sin θ » θ = \(\frac{arc}{radius}=\frac{AB}{OB} =\frac{x}{L}\) ∴ F = − mgθ = − mg\(\frac{x}{L}\) ….(1) Since m, g and L are constant, ∴ F ∝ (−x) …….(2) Thus, the net force on the bob is in the direction opposite to that of displacement x of the bob from its mean position as indicated by the minus sign, and the magnitude of the force is proportional to the magnitude of the displacement. Hence, it follows that the motion of a simple pendulum is linear SHM. Acceleration, a = F/m = \(\frac{g}{L}x\) ......(3) Therefore, acceleration per unit displacement \(\left | \frac{a}{x} \right |=\frac{g}{L} \) Period of SHM, T = \(\frac{2π}{\sqrt{\text{acceleration per unit displacement}}}=\frac{2π}{\sqrt{g/L}}\) ∴ T = \(2π\sqrt{L/g}\) This gives the expression for the period of a simple pendulum.
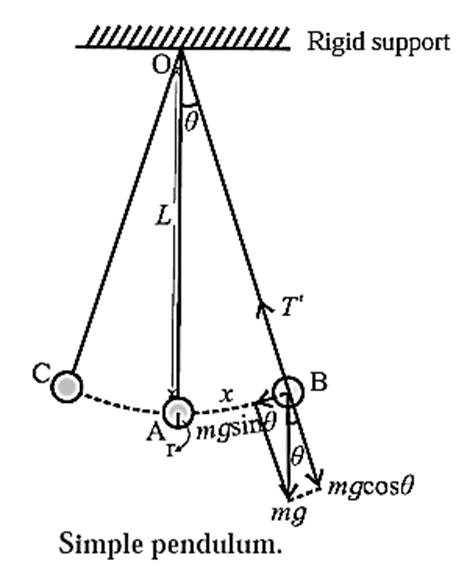
iv) State the laws of simple pendulum.
The period of a simple pendulum at a given place is T = \(2π\sqrt{L/g}\) where L is the length of the simple pendulum and g is the acceleration due to gravity at that place. From the above expression, the laws of simple pendulum are as follows Law of length :The period of a simple pendulum at a given place (g constant) is directly proportional to the square root of its length. T ∝ \(\sqrt{L}\) Law of mass :The period of a simple pendulum does not depend on the mass or material of the bob of the pendulum. Law of acceleration due to gravity : The period of a simple pendulum of a given length (L constant) is inversely proportional to the square root of the acceleration due to gravity. T ∝ \(\sqrt{\frac{1}{g}}\) Law of isochronism :The period of a simple pendulum does not depend on the amplitude of oscillations, provided that the amplitude is small.
v) Prove that under certain conditions a magnet vibrating in uniform magnetic field performs angular S.H.M.
Consider a bar magnet of magnetic moment μ, suspended horizontally by a light twistless fibre in a region where the horizontal component of the Earth's magnetic field is B. The bar magnet is free to rotate in a horizontal plane. It comes to rest in approximately the North—South direction, along B. If it is rotated in the horizontal plane by a small displacement θ from its rest position (θ =0),the suspension fibre is twisted. When the magnet is released, it oscillates about the rest position in angular or torsional oscillation. The bar magnet experiences a torque r due to the field B. Which tends to restore it to its original orientation parallel to B. For small θ, this restoring torque is τ = −μB sin θ = −μBθ ...(1) where the minus sign indicates that the torque is opposite in direction to the angular displacement θ. Equation (1) shows that the torque (and hence the angular acceleration) is directly proportional in magnitude of the angular displacement but opposite in direction. Hence, for small angular displacment, the oscillations of the bar magnet in a uniform magnetic field is simple harmonic.
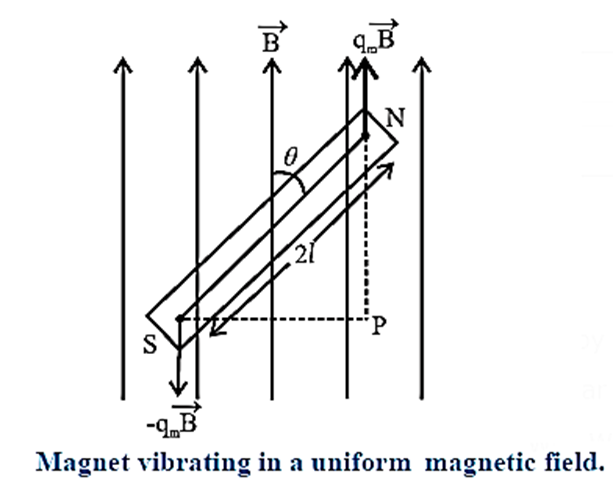
Question 3.
Obtain the expression for the period of a magnet vibrating in a uniform magnetic field and performing S.H.M.
Consider a bar magnet of magnetic moment μ, suspended horizontally by a light twistless fibre in a region where the horizontal component of the Earth's magnetic field is B. The bar magnet is free to rotate in a horizontal plane. It comes to rest in approximately the North—South direction, along B. If it is rotated in the horizontal plane by a small displacement θ from its rest position (θ =0),the suspension fibre is twisted. When the magnet is released, it oscillates about the rest position in angular or torsional oscillation. The bar magnet experiences a torque r due to the field B. Which tends to restore it to its original orientation parallel to B. For small θ, this restoring torque is τ = −μB sin θ = −μBθ ...(1) where the minus sign indicates that the torque is opposite in direction to the angular displacement θ. For clockwise angular displacement θ , the restoring torque is in the anticlockwise direction. ∴ τ = Iα = −μBθ where I is the moment of inertia of the bar magnet and a is its angular acceleration. ∴ α = −μBθ/I --- (1) Since μ, B and I are constants, Eq. (1) shows that angular acceleration is directly proportional to the angular displacement and directed opposite to the angular displacement. Hence the magnet performs angular S.H.M. The period of vibrations of the magnet is given by ∴ T = \(\frac{2π}{\sqrt{α/θ}}=\frac{2π}{\sqrt{\text{angular acceleration per unit angular displacement}}}\) ∴ T = \(\frac{2π}{\sqrt{α/θ}} = 2π\sqrt{\frac{I}{−μB}\)

Question 4.
Show that a linear S.H.M. is the projection of a U.C.M. along any of its diameter.
Consider a particle which moves anticlockwise around a circular path of radius r with a constant angular speed w (Fig). Let the path lie in the x-y plane with the centre at the origin O. The instantaneous position P of the particle is called the reference point and the circle in which the particle moves as the reference circle. The perpendicular projection of P onto the y-axis is Q. Then, as the particle travels around the circle, Q moves to-and-fro along the y-axis. Line OP makes an angle a with the x-axis at t= 0. At time t, this angle becomes θ = ωt + α. The projection Q of the reference point is described by the y-coordinate, y = OQ = OP sin ∠OPQ, Since ∠OPQ = ωt + α. y = r sin(ωt + α.) which is the equation of a linear SHM of amplitude A. The angular frequency w of a linear SHM can thus be understood as the angular velocity of the reference particle. Projection of velocity: The tangential velocity of the reference particle is v = ωr. Its y-component at time t is‘ vy = ωr sin (90°− θ) = ωr cos θ vy = ωr cos (ωt + α) Projection of acceleration: The centripetal acceleration of the reference particle is ar = ω2r , so that its y-component at time t is ax = ar sin ∠OPQ ∴ ax = − ω2r sin (ωt + α) = − ω2y

Question 5.
Draw graphs of displacement, velocity and acceleration against phase angle, for a particle performing linear S.H.M. from (a) the mean position (b) the positive extreme position. Deduce your conclusions from the graph.
(a) Conclusions from the graphs for the mean position: (v) Conclusions for positive extreme position : Graph :

Question 6.
Deduce the expressions for the kinetic energy and potential energy of a particle executing S.H.M. Hence obtain the expression for total energy of a particle performing S.H.M and show that the total energy is conserved. State the factors on which total energy depends.
Consider a particle of mass m performing linear SHM with amplitude A. The restoring force acting on the particle is P = −kx, where k is the force constant and x is the displacement of the particle from its mean position. Kinetic energy : At distance x from the mean position, the velocity is v = \(ω\sqrt{A^2−x^2}\) where ω = \sqrt{\frac{k}{m}}\) . The kinetic energy (KE) of the particle is KE = ½ mv2 = ½ mω2(A2 − x2) = ½ k(A2 − x2) ……..(1) If the phase of the particle at an instant t is 0 = ωt + α, where a is initial phase, its velocity at that instant is v = ωA cos (ωt + α) and its KE at that instant is KE = ½ mv2 = ½ mω2A2 cos2(ωt + α) = ½ kA2 cos2(ωt + α) …..(2) Therefore, the KE varies with time as cos2θ . Potential energy : The potential energy of a particle in linear SHM is defined as the work done by an external agent, against the restoring force, in taking the particle from its mean position to a given point in the path, keeping the particle in equilibrium. Suppose the particle in fig. is displaced from P1 to P2, through an infinitesimal distance dx against the restoring force F as shown. The corresponding work done by the external agent will be dW = (- F )dx = kx dx. This work done is stored in the form of potential energy. The potential energy (PE) of the particle when its displacement from the mean position is x can be found by integrating the above expression from 0 to x. ∴ PE = \(\int dW =\int kx\,dx =\frac{1}{2}dx^2 \) The displacement of the particle at an instant t being P x = A sin (ωt + α) its PE at that instant is PE = ½ kx2 = ½ kA2 sin (ωt + α) …….(4) Therefore, the PE varies with time as sin2θ. Total energy : The total energy of the particle is equal to the sum of its potential energy and kinetic energy. From Eqs. (1) and (2), total energy is E = PE + KE = ½ kx2 + ½ k(A2 – x2) = ½ kx2 + ½ kA2 – ½ k x2 = ½ kA2 = ½ mω2A2 = …….(5) Total energy of SHM in terms of acceleration is E = ½ mω2A2 = ½ mAamax (….amax = ω2A) ∴ E = ½ mAamax is the the expression of total energy in terms of acceleration. As m is constant, and ω and A are constants of the motion, the total energy of the particle remains constant (or its conserved). Factors on which the total energy of a particle executing SHM depends : If η is the frequency in S.H.M. ω = 2πη and for T is the period of the motion w = 2π/T Using this in Eq. (5), we get = 2π2mη2A2 = \(\frac{2π^2mA^2}{T^2}\) Conclusions :The total energy of the particle is
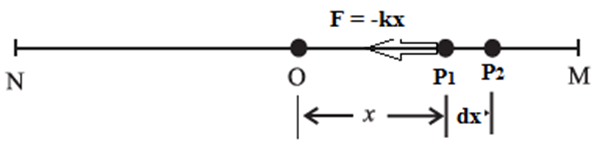
Question 7.
Deduce the expression for period of simple pendulum. Hence state the factors on which its period depends.
Consider a simple pendulum of length L, suspended from a rigid support O. When displaced from its initial position of rest through a small angle q in a vertical plane and released, it performs oscillations between two extremes, B and C, as shown in Fig. At B, the forces on the bob are its weight mg and the tension T’ in the string. Resolve mg into two components : mg cos θ in the direction opposite to that of the tension and mg sin θ perpendicular to the string. mg cos θ is balanced by the tension in the string. mg sin θ restores the bob to the equilibrium position. Restoring force, F = − mg sin θ If θ is small and expressed in radian, sin θ » θ = \(\frac{arc}{radius}=\frac{AB}{OB} =\frac{x}{L}\) ∴ F = − mgθ = − mg\(\frac{x}{L}\) ….(1) Since m, g and L are constant, ∴ F ∝ (−x) …….(2) Thus, the net force on the bob is in the direction opposite to that of displacement x of the bob from its mean position as indicated by the minus sign, and the magnitude of the force is proportional to the magnitude of the displacement. Hence, it follows that the motion of a simple pendulum is linear SHM. Acceleration, a = F/m = \(\frac{g}{L}x\) ......(3) Therefore, acceleration per unit displacement \(\left | \frac{a}{x} \right |=\frac{g}{L} \) Period of SHM, T = \(\frac{2π}{\sqrt{\text{acceleration per unit displacement}}}=\frac{2π}{\sqrt{g/L}}\) ∴ T = \(2π\sqrt{L/g}\) This gives the expression for the period of a simple pendulum. From the above expression, the factors on which its period depends.

Question 8.
At what distance from the mean position is the speed of a particle performing S.H.M. half its maximum speed. Given path length of S.H.M. = 10 cm.
Given : v = \(\frac{1}{2}v_max\) , 2A=10 cm A=5 cm v = \(ω\sqrt{A^2-x^2}\) and vmax = ωA Since v = \(\frac{1}{2}v_max\) \(ω\sqrt{A^2-x^2}=\frac{ωA}{2}\) ∴ \(A^2-x^2=\frac{A^2}{4}\) ∴ \(x^2=A^2-\frac{A^2}{4} = \frac{3A^2}{4} \) ∴ \(x= ±\frac{\sqrt{3}}{2}A\) = 0.866 x 5= ± 4.33 cm This gives the required displacement.
Question 9.
In SI units, the differential equation of an S.H.M. is \(\frac{d^2x}{dt^2}=-36x\) . Find its frequency and period.
Given : \(\frac{d^2x}{dt^2}=-36x\) Comparing this equation with the general equation, We get, ω2 = 36, ∴ ω = 6 rad/s ω = 2πη The frequency, η = ω/2π = 6/(2x3.142) = 0.9548 Hz and the period, T = 1/η = 1/0.9548 = 1.047s
Question 10.
A needle of a sewing machine moves along a path of amplitude 4 cm with frequency 5 Hz. Find its acceleration 1/30 s after it has crossed the mean position.
Given : A=4 cm = 4 x 10-2m, η = 5Hz, t= 1/30 s ω = 2πη = 2π x 5 = 10π rad/s Therefore, the magnitude of the acceleration, |a| = ω2x = ω2A sin ωt = (10π)2 (4 X 10-2) sin 10π/30 = 4π2 sin π/3 = 4 (9.872)(0.866) = 34.20 m/s2
Question 11.
Potential energy of a particle performing linear S.H.M is 0.1 π2 x2 joule. If mass of the particle is 20 g, find the frequency of S.H.M.
Given : PE = 0.1π2x2 J, m = 20 g = 2 X 10-2 kg PE = ½ mw2x2 = ½m(4π2η2)x2 = 0.1π2x2 ∴ 2mη2 = 0.1 ∴ η2 = 0.1/[2(2 X 10-2)]= 2.5 ∴ The frequency of SHM is η = \(\sqrt{2.5}\) = 1.581 Hz
Question 12.
The total energy of a body of mass 2 kg performing S.H.M. is 40 J. Find its speed while crossing the centre of the path.
Given : m = 2 kg, E = 40 J The speed of the body while crossing the centre of the path (mean position) is vmax and the total energy is entirely kinetic energy. \(\frac{1}{2}\)mv2max = E ∴ vmax = \(\sqrt{\frac{2E}{m}}= \sqrt{\frac{2×40}{2}}\) = 6.324 m/s
Question 13.
A simple pendulum performs S.H.M of period 4 seconds. How much time after crossing the mean position, will the displacement of the bob be one third of its amplitude.
Given : T = 4 s, x = A/3 The displacement of a particle starting into SHM from the mean position is x =A sin ωt = A sin(2π/T)t ∴ A sin(2π/T)t = A/3 ∴ (2π/T)t = sin-1 0.3333 = 19.47° = 19.47 x π/180 rad ∴ t = 19.47/90 = 0.2163s ∴ The displacement of the bob will be one-third of its amplitude 0.2163s after crossing the mean position.
Question 14.
A simple pendulum of length 100 cm performs S.H.M. Find the restoring force acting on its bob of mass 50 g when the displacement from the mean position is 3 cm.
Given : L = 100cm, m = 50 g = 5 x 10−2 kg, x = 3 cm, g = 9.8 m/s2 Restoring force, F = mg sin θ = mgθ = (5 x 10−2)(9.8)(3/100) = 1.48 x 10−2N
Question 15.
Find the change in length of a second’s pendulum, if the acceleration due to gravity at the place changes from 9.75 m/s2 to 9.8 m/s2.
Given : g1 =9.75 m/s2, g2 = 9.8 m/s2 Length of a seconds pendulum, L = g/π2 ∴ L1 = g1/π2 = 9.75/9.872 = 0.9876 m and ∴ L2 = g2/π2 = 9.8/9.872 = 0.9927 m The length of the seconds pendulum must be increased from 0.9876 m to 0.9927 m, i.e., (0.9927−0.9876) by 0.0051 m.
Question 16.
At what distance from the mean position is the kinetic energy of a particle performing S.H.M. of amplitude 8 cm, three times its potential energy?
Given : A=8 cm, KE = 3PE KE = \(\frac{1}{2}\)k(A2 —x2) and PE = \(\frac{1}{2}\)kx2 Given, KE = 3PE. ∴ \(\frac{1}{2}\) k(A2 —x2) = 3( \(\frac{1}{2}\) kx2) ∴ A2 —x2 = 3x2 , ∴ 4x2 = A2 the required displacement is x = ± A/2 = ±8/2 = ±4 cm
Question 17.
A particle performing linear S.H.M. of period 2p seconds about the mean position O is observed to have a speed of \(b\sqrt{3}\) m / s , when at a distance b (metre) from O. If the particle is moving away from O at that instant, find the time required by the particle, to travel a further distance b.
Given : T = 2π s, v = \(b\sqrt{3}\) m/s at x=b ω = 2π/T = 2π/2π =1 rad/s v = ω\(\sqrt{A^2-x^2}\) ∴ at x = b, \(b\sqrt{3}\) = (1)\(\sqrt{A^2-x^2}\) ∴ 3b2 = A2 – b2 , ∴ A = 2b ∴ Assuming the particle starts from the mean position, its displacement is given by x = A sin ωt = 2b sint If the particle is at x = b at t = t1, b = 2b sin t1 ∴ t1= sin-1(1/2) = π/6 s Also, with period T = 2π s, on travelling a further distance b the particle will reach the positive extremity at time t2 = π/2 s. The time taken to travel a further distance b from x = b is t2 – t1 = π/2 − π/6 = π/3 s
Question 18.
The period of oscillation of a body of mass m1 suspended from a light spring is T. When a body of mass m2 is tied to the first body and the system is made to oscillate, the period is 2T. Compare the masses m1 and m2
For mass m1, period is T ∴ T = 2π\(\sqrt{\frac{m_1}{k}}\) For mass m2, period is 2T ∴ 2T = 2π\(\sqrt{\frac{m_1+m_2}{k}}\) ∴ 2T/T = 2 = \(\sqrt{\frac{m_1+m_2}{m_1}}\) ∴ \(\frac{m_1+m_2}{m_1}\) = 4 ∴ \(\frac{m_2}{m_1}\) = 3 ∴ \(\frac{m_1}{m_2}\) = \(\frac{1}{3}\)
Question 19.
The displacement of an oscillating particle is given by x= a sin ωt + b cos ωt where a, b and ω are constants. Prove that the particle performs a linear S.H.M. with amplitude A = \(\sqrt{a^2+b^2}\)
x= a sin ωt + b cos ωt Let a = A cos ∅ and b = A sin ∅, so that A2 = a2 + b2 and tan ∅ = b/a x=A cos ∅ sin ωt + A sin ∅ cos ωt x = A sin (ωt+∅) which is the equation of a linear SHM with amplitude A = \(\sqrt{a^2+b^2}\) and phase constant ∅ = tan-1(b/a) as required.
Question 20.
Two parallel S.H.M.s represented by x1 = 5sin (4πt + π/3) cm and x2 = 3sin (4πt + π/4) cm are superposed on a particle. Determine the amplitude and epoch of the resultant S.H.M.
Given : x1 = 5sin (4πt + π/3) = A1 sin(ωt + α), x2 = 3sin (4πt + π/4) = A2 sin(ωt + β), ∴ A1 =5 cm, A2 =3 cm, α = π/3 rad, β = π/4 rad (i) Resultant amplitude, R = \(\sqrt{A_1^2+A_2^2+2A_1A_2cos(α-β)}\) ∴ R = \(\sqrt{5^2+3^2+2(5)(3)cos(π/3-π/4)}\) = \(\sqrt{25+9+30cos(π/3-π/4)} = \sqrt{62.98}\) = 7.936 cm (ii) Epoch of the resultant SHM, δ = \(tan^{-1}(\frac{A_1sinα+A_2sinβ}{A_1cosα+A_2cosβ})\) = \(tan^{-1}(\frac{5sin(π/3)+3sin(π/4)}{5cos(π/3)+3cos(π/4)})\) = \(tan^{-1}(\frac{5(0.866)+3(0.7071)}{5(0.5)+3(0.7071)})\) = \(tan^{-1}(1.396)\) = 54023’
Question 21.
A 20 cm wide thin circular disc of mass 200 g is suspended to a rigid support from a thin metallic string. By holding the rim of the disc, the string is twisted through 60o and released. It now performs angular oscillations of period 1 second. Calculate the maximum restoring torque generated in the string under undamped conditions. (π3 ≈ 31)
Given: R = 10cm = 0.1 m, M = 0.2 kg, θm=600 = p/3 rad, T=1 s, π3 = 31 The MI of the disc about the rotation axis (perpendicular through its centre) is I = ½ MR2 = ½ (0.2)(0.1)2 = 10-3 kg-m2 The period of torsional oscillation, T = 2π\(\sqrt{\frac{I}{c}}\) ∴ The torsion constant, c = 4π2\(\frac{I}{T^2}\) The magnitude of the maximum restoring torque, τmax = cθm = 4π2\(\frac{I}{T^2}(\frac{π}{3})\) = \(\frac{4}{3}π^3\frac{I}{T^2}=\frac{4}{3}(31)(\frac{10^{-3}}{1^2})\) = 41.33 x 10-3 = 0.04133 N-m
Question 22.
Find the number of oscillations performed per minute by a magnet is vibrating in the plane of a uniform field of 1.6 × 10-5 Wb/m2. The magnet has moment of inertia 3 × 10-6 kg/m2 and magnetic moment 3 A-m2.
Given: B =1.6 x 10-5 T, I = 3 x 10-6 Kg/m2, m =3 A-m2 The period of oscillation, T = 2π\(\sqrt{\frac{I}{μB}}\) ∴ The frequency of oscillation is η = \(\frac{1}{2π}\sqrt{\frac{μB}{I}}\) The number of oscillations per minute 60η =\(\frac{60}{2π}\sqrt{\frac{(3)(1.6×10^{-5})}{3×10^{-6}}}\) =\(\frac{60}{2π}\sqrt{16}\) = 38.19 per minute
Question 23.
A wooden block of mass m is kept on a piston that can perform vertical vibrations of adjustable frequency and amplitude. During vibrations, we don’t want the block to leave the contact with the piston. How much maximum frequency is possible if the amplitude of vibrations is restricted to 25 cm? In this case, how much is the energy per unit mass of the block? (g ≈ π2 ≈ 10 m s2)
Given : A = 0.25m, g = π2 = 10 m s2 During vertical oscillations, the acceleration is maximum at the turning points at the top and bottom. The block will just lose contact with the piston when its apparent weight is zero at the top, i.e., when its acceleration is amax = g, downwards. |amax| = ω2A = 4π2 η2max A = g ∴ η2max = \(\sqrt{\frac{g}{4π^2A}}\) = \(\sqrt{\frac{10}{4×10×0.25}}\) = 1 Hz This gives the required frequency of the piston. E = ½ mω2A2 = ½ m(4π2 η2)A2 ∴ E/m = 2p2 h2A2 = 2 x 10 x 12 x (1/4)2 = 1.25 J/kg
Download PDF from store : Class-12-Physics-Chapter-5-Oscillations–Text Book Get PDF from store : Class-12-Physics-Chapter-5-Oscillations–Notes Get PDF from store : Class-12-Physics-Chapter-5-Oscillations–Solution
Main Page : – Maharashtra Board Class 12th-Physics – All chapters notes, solutions, videos, test, pdf. Previous Chapter : Chapter-4-Thermodynamics –Online Solution Next Chapter : Chapter-6-Superposition of Waves – Online Solution
We reply to valid query.