Superposition of Waves
Maharashtra Board-Class-12th-Physics-Chapter-6
Notes-Part-2
Topics to be Learn : Part-2
|
Harmonics and overtones :
- A stationary wave is set up in a bounded medium in which the boundary could be a rigid support (i.e., a fixed end, as for instance a string stretched between two rigid supports) or a free end (as for instance an air column in a cylindrical tube with one or both ends open). The boundary conditions limit the possible stationary waves and only a discrete set of frequencies is allowed.
- The lowest allowed frequency n1 is called the fundamental frequency of vibration. Integral multiples of the fundamental frequency are called the harmonics, the fundamental frequency being called the first harmonic. The second harmonic is twice the fundamental or 2n1, the third harmonic is 3n1, and so on.
- The higher allowed harmonics above the first harmonic or fundamental are called overtones. The first overtone is the higher allowed harmonic immediately above the first harmonic.
- Above the fundamental, the first allowed frequency is called the first overtone, the next higher frequency is the second over-tone, and so on. The relation between overtones and allowed harmonics depends on the system under consideration.
End correction and the cause of end correction. When sound waves are sent down the air column in a narrow closed or open pipe, they are reflected at the ends —without phase reversal at an open end and with a phase reversal at a closed end. Interference between the incident and reflected waves under appropriate conditions sets up stationary waves in the air column. Thus, the stationary waves have an antinode at an open end. However, because air molecules in the plane of an open end are not free to move in all direflection of the longitudinal waves takes place slightly beyond the rim of the pipe at an open end. The distance of the antinode from the open end of the pipe is called end correction. Estimation of end correction: According to Reynolds, the distance of the antinode from the rim is approximately 30% of the inner diameter of a cylindrical pipe. This distance must be taken into account in accurate determination of the wavelength of sound. Hence, this distance is called the end correction. Therefore, if d is the inner diameter of a cylindrical pipe, an end correction e = 0.3d for each open end must be added to the measured length of the pipe. If l is the measured length, the effective length of the air column in the case of a pipe closed at one end is l + 0.3d, while that for a pipe open at both ends is l + 0.6d. ∴ For a pipe closed at one end The corrected length of air column L = l + e And for a pipe open at both ends L = l + 2e
Vibrations of air column in a pipe closed at one end : Consider a narrow cylindrical pipe of length l closed at one end. When sound waves are sent down the air column in a cylindrical pipe closed at one end, they are reflected at the closed end with a phase reversal and at the open end without phase reversal. Interference between the incident and reflected waves under appropriate conditions sets up stationary waves in the air column. The stationary waves in the air column in this case are subject to two boundary conditions that there must be a node at the closed end and an antinode at the open end. Taking into account the end correction e at the open end, the resonating length of the air column is L = l + e. Let v be the speed of sound in air. In the simplest mode of vibration [Fig.(a)] there is a node at the closed end and an antinode at the open end. The distance between a node and a consecutive antinode is λ/4 , where λ is the wavelength of sound. The corresponding wavelength λ and frequency n are Λ = 4L and n = \(\frac{v}{λ} = \frac{v}{4L}=\frac{v}{4(l+e)}\) …..(1) This gives the fundamental frequency of vibration and the mode of vibration is called the fundamental mode or first harmonic. In the next higher mode of vibration, the first overtone, two nodes and two antinodes are formed [Fig.(b) ]. The corresponding wavelength λ1 and frequency n1 are and n1 = v/λ1 = 3v/4L = \(\frac{3v}{4(l+e)}\) = 3n ……(2) Therefore, the frequency in the first overtone is three times the fundamental frequency, i.e., the first overtone is the third harmonic. In the second overtone, three nodes and three antinodes are formed [Fig (c)]. The corresponding wavelength λ2 and frequency n2 are λ2 = \(\frac{4L}{5}\) and n2 = v/λ2 = 5v/4L = \(\frac{5v}{4(l+e)}\) = 5n ….(3) which is the fifth harmonic, Therefore, in general, the frequency of the pth overtone (p = 1, 2, 3, ...) is np= (2P+1)n …..(4) i.e., the pth overtone is the (2p + 1)th harmonic. Equations (1), (2) and (3) show that allowed frequencies in an air column in a pipe closed at one end are n, 3n, 5n, ….. That is, only odd harmonics are present as overtones.
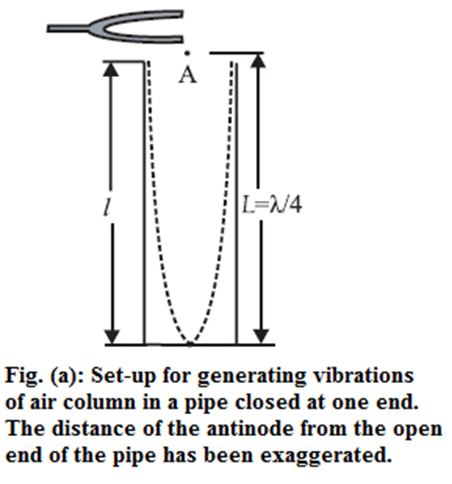

Vibrations of air column in a pipe open at both ends: Consider a cylindrical pipe of length l open at both the ends. When sound waves are sent down the air column in a cylindrical open pipe, they are reflected at the open ends without a change of phase. Interference between the incident and reflected waves under appropriate conditions sets up stationary waves in the air column. The stationary waves in the air column in this case are subject to the two boundary conditions that there must be an antinode at each open end. Taking into account the end correction e at each of the open ends, the resonating length of the air column is L= l +2e. Let v be the speed of sound in air. In the simplest mode of vibration, the fundamental mode or first harmonic, there is a node midway between the two antinodes at the open ends [Fig. (a)]. The distance between two consecutive antinodes is λ/2, where λ is the wavelength of sound. The corresponding wavelength λ and the fundamental frequency n are λ = 2L and n = v/λ = v/2L = \(\frac{v}{2(l+2e)}\) …..(1) In the next higher mode, the first overtone, there are two nodes and three antinodes [Fig.(b)]. The corresponding wavelength λ1 and frequency n1 λ1 = L and n1 = v/λ1 = v/L = \(\frac{v}{l+2e}\) =2n …..(2) i.e., twice the fundamental. Therefore, the first overtone is the second harmonic. In the second overtone, there are three nodes and four antinodes [Fig. (c)]. The corresponding wavelength λ2 and frequency n2 are λ2 = 2L/3 and n2 = v/λ2 = \(\frac{3v}{2L}\) = \(\frac{3v}{2(l+2e)}\) = 3n …..(3) or thrice the fundamental. Therefore, the second overtone is the third harmonic. Therefore, in general, the frequency of the pth overtone (p = 1, 2, 3, ...) is np=(p+1)n ….(4) i.e., the pth overtone is the (p + 1)th harmonic. Equations (1), (2) and (3) show that allowed frequencies in an air column in a pipe open at both ends are n, 2n, 3n. That is, all the harmonics are present as overtones.
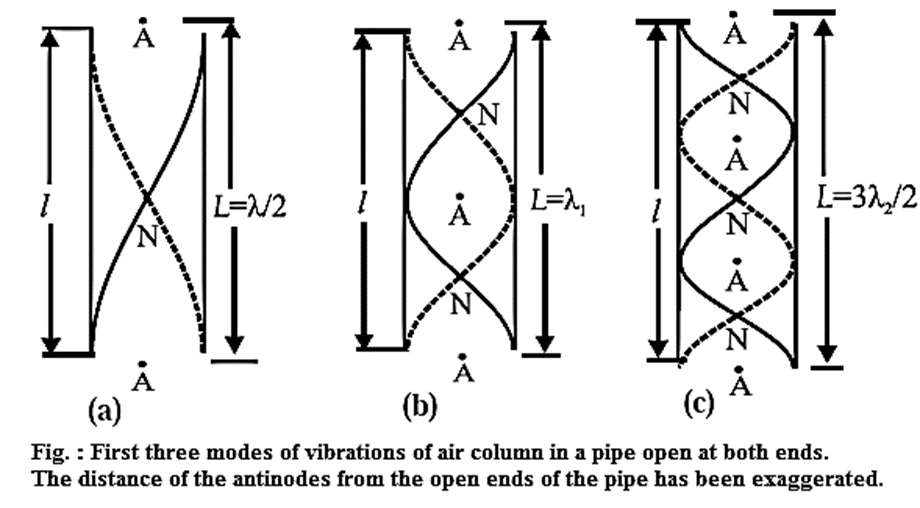
Q. What are the frequencies of the notes produced in an open and closed pipes in terms of the length of pipe L and velocity of waves v?.
The frequencies of all the harmonics present in an open pipe are n = (P+1)\(\frac{v}{4L}\) = (P+1)\(\frac{v}{4(l+2e)}\) where p =0, 1, 2, 3, . The frequencies of the odd harmonics present in a closed pipe are n = (2P+1)\(\frac{v}{4L}\) = (2P+1)\(\frac{v}{4(l+e)}\) where p =0, 1, 2, 3,….
Q. Two organ pipes closed at one end have the same diameters but different lengths. Show that the end correction at each end is e = \(\frac{n_1l_1-n_2l_2}{n_2-n_1}\). where the symbols have their usual meanings.
Suppose two organ pipes, closed at one end and of the same inner diameter d have lengths l1 and l2 Then the effective lengths of the air columns are respectively L1 = l1+e = l1+0.3d and L2 = l2 +e = l2 +0.3d where e=0.3d is the end correction for the open end. The fundamental frequencies of the corresponding air columns are n1 = \(\frac{v}{4L_1}\) = \(\frac{v}{4(l_1+e)}\) and n2 = (\frac{v}{4L_2}\) = \(\frac{v}{4(l_2+e)}\) where v is the speed of sound in air. ∴ v = 4n1(l1+e) = 4n2(l2+e) ∴ n1l1+ n1e = n2l2+ n2e ∴ n1l1 - n2l2 = (n2 – n1)e ∴ e = \(\frac{n_1l_1-n_2l_2}{n_2-n_1}\) which is the required expression.
Q. Two organ pipes open at both ends have the same diameters but different lengths. Show that the end correction at each end is e = \(\frac{n_1l_1-n_2l_2}{2(n_2-n_1)}\) where the symbols have their usual meanings.
Suppose two organ pipes, open at both ends and same inner diameter d, have lengths l1 and l2. Then, the effective lengths of the air columns are respectively L1 = l1+2e = l1+0.6d and L2 = l2 +2e = l2 +0.6d where e=0.3d is the end correction for each open end. The fundamental frequencies of the corresponding air columns are n1 = \(\frac{v}{2L_1}\) = \(\frac{v}{2(l_1+2e)}\) and n2 = \(\frac{v}{2L_2}\) = \(\frac{v}{2(l_2+e)}\) where v is the speed of sound in air. ∴ v = 2n1(l1+2e) = 2n2(l2+2e) ∴ n1l1+ 2n1e = n2l2+ 2n2e ∴ n1l1 - n2l2 = 2(n2 – n1)e ∴ e = \(\frac{n_1l_1-n_2l_2}{2(n_2-n_1)}\) which is the required expression.
| Remember :For correct value of end correction, the inner diameter of pipe must be uniform throughout its length. It may be noted that effect of flow of air and effect of temperature of air outside the tube has been neglected. |
Limitations of end correction :
- Inner diameter of the tube must be uniform.
- Effects of air flow and temperature outside the tube are ignored.
- The prongs of the tuning fork should be perpendicular to the air column in the tube, with their tips at the centre of the tube and a small distance above the rim of the tube.
Remember : A tuning fork is in resonance with a closed pipe, but the same tuning fork cannot be in resonance with an open pipe of the same length. Because for the same length of air column, and the same speed of sound, the fundamental frequency of the air column in a closed pipe is half that in an open pipe. Hence, a tuning fork in unison with the air column in a closed pipe cannot be in unison with the air column of the same length in an open pipe.
Vibrations Produced in a String:
(i) If a string (or a wire) stretched between two rigid supports is plucked at some point, the disturbance produced travels along the string in the form of transverse waves.
If T is the tension applied to the string and m is the mass per unit length (i.e., linear density) of the string, the speed of the transverse waves is
- v = \(\sqrt{\frac{T}{m}}\)
(ii) The transverse waves moving along the string are reflected from the supports. The reflected waves interfere and under certain conditions set up stationary waves in the string. At each support, a node is formed.
(iii) The possible or allowed stationary waves are subject to the two boundary conditions that there must be a node at each fixed end of the string. The different ways in which the string can then vibrate are called its modes of vibration.
In the simplest mode of vibration, there are only two nodes (N), one at each end and an antinode (A) is formed midway between them, as shown in fig.
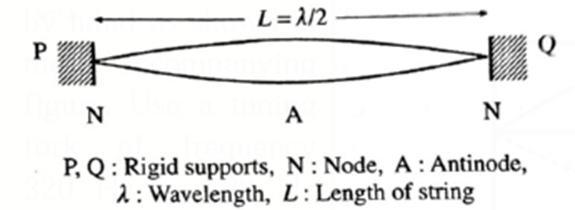
In this case, the distance between successive nodes is equal to the length of the string (L) and is equal to λ/2, where λ is the wavelength.
∴ L= λ/2 or λ = 2L
The frequency of vibrations is n = v/ λ
Substituting v = \(\sqrt{\frac{T}{m}}\) and λ = 2L in this relation,
we get,
n = \(\frac{1}{2L}\sqrt{\frac{T}{m}}\)
This is the lowest frequency of the stationary waves on a stretched string and is called the fundamental frequency.
Three lowest modes of vibration of a string stretched between rigid supports : Consider a string of linear density m stretched between two rigid supports a distance L apart. Let T be the tension in the string. Stationary waves set up on the string are subjected to two boundary conditions, the displacement y = 0 at x = 0 and at x = L at all times. That is, there must be a node at each fixed end. These conditions limit the possible modes of vibration to only a discrete set of frequencies such that there are an integral number of loops p between the two fixed ends. Since, the length of one loop (the distance between consecutive nodes) corresponds to half a wavelength (λ), L/p = λ/2, ∴ λ = 2L/p ….(1) The speed of a transverse wave on a stretched string is v = nλ = \(\sqrt{\frac{T}{m}}\) ……(2) Therefore, from Eqs. (1) and (2), the allowed frequencies are given by n = \(\frac{p}{2L}\sqrt{\frac{T}{m}}\) where p=1, 2,3,…. (3) In the simplest mode of vibration, only one loop (p = 1) is formed [Fig.(a)]. The corresponding lowest allowed frequency, n, given by n = \(\frac{1}{2L}\sqrt{\frac{T}{m}}\) …..(4) is called the fundamental frequency or the first harmonic. The possible modes of vibration with frequencies higher than the fundamental are called the overtones. In the first overtone, two loops are formed (p = 2) [Fig (b)]. Its frequency, n1 = \(\frac{2}{2L}\sqrt{\frac{T}{m}}\) = 2n …..(5) is twice the fundamental and is, therefore, the second harmonic. In the second overtone, three loops are formed (p = 3) [Fig. (c)]. Its frequency, n2 = \(\frac{3}{2L}\sqrt{\frac{T}{m}}\) = 3n …..(6) is the third harmonic. Therefore, in general, the frequency of the pth overtone (p = 1, 2, 3, ...) is np = (p+1)n ……(7) i.e., the pth overtone is the (p + 1)th harmonic. Equation (3) gives the set of discrete frequencies for the normal modes of vibration of a stretched string. Equation (7) shows that for a stretched string all the harmonics are present as overtones.
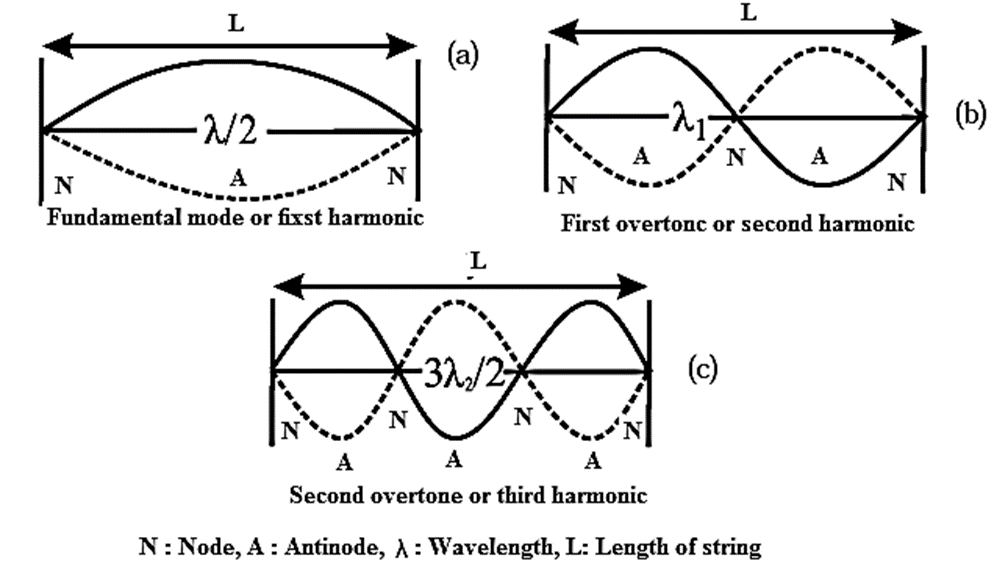
- Nodes are the points where the vibrating string can be touched without disturbing its motion.
- When the string vibrates in its fundamental mode, the string vibrates in one loop. There are no nodes formed between the fixed ends. Hence, there are no point on the string which can be touched without disturbing its motion.
- When the string vibrates in its first overtone (second harmonic), there are two loops of the stationary wave on the string. Apart from the two nodes at the two ends, there is now a third node at its centre. Hence, the string can be touched at its centre without disturbing the stationary wave pattern.
- When the string vibrates in its second overtone (third harmonic), there are three loops of the stationary wave on the string. So, apart from the two end nodes, there are two additional nodes in between, at distances one-third of the string length from each end. Thus, now the string can be touched at these two nodes.
Laws of a Vibrating String : The fundamental frequency of a vibrating string under tension is given as n = \(\frac{1}{2L}\sqrt{\frac{T}{m}}\) From this formula, three laws of vibrating string can be given as follows: 1) Law of length: The fundamental frequency of vibrations of a string is inversely proportional to the length of the vibrating string, if tension and mass per unit length are constant. if T and m are constant n ∝ 1/L 2) Law of tension: The fundamental frequency of vibrations of a string is directly proportional to the square root of tension, if vibrating length and mass per unit length are constant. If L and m are constant. n ∝ \(\sqrt{T}\) 3) Law of linear density: The fundamental frequency of vibrations of a string is inversely proportional to the square root of mass per unit length (linear density), if the tension and vibrating length of the string are constant. If T and L are constant n ∝ \(\sqrt{\frac{1}{m}}\)
Fundamental frequency of a vibrating string depend on the radius of cross section of the string and the mass density of the material of the string :
Explanation : Consider a string stretched between two rigid supports a distance L apart. Let T be the tension in the string, r be its radius of cross section and ρ be the mass density of its material. Then, the mass of the string M = (πr2L)ρ, so that its linear density, i.e., mass per unit length, m = M/L = πr2ρ According to the law of mass of a vibrating string, the fundamental frequency (n) is inversely proportional to the square root of its linear density, when T and L are constant. n ∝ \(\frac{1}{\sqrt{m}}\) ∴ n ∝ \(\frac{1}{\sqrt{πr^2ρ}}\) n ∝ 1/r, when L, T and ρ are constant, and n ∝ \(\frac{1}{\sqrt{ρ}}\) , when L, T and r are constant. Hence fundamental frequency of the string/wire depends on
Sonometer:
A sonometer consists of a uniform wire stretched over a rectangular sounding box, and passes over two movable bridges (or knife edges) and a pulley, see Fig.
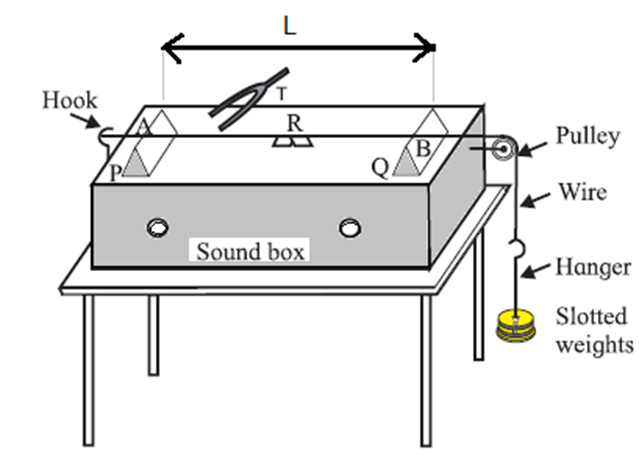
- It works on the phenomenon of resonance.
- The tension in the wire is adjusted by adding weights to the hanger attached to the free end of the wire.
- The length of the wire between the movable bridges, L, is adjusted to vibrate in unison with a given tuning fork either by beats method or by paper—rider method.
- L is called the vibrating length.
- First, the vibrating length is set to minimum and then gradually increased in small steps.
In the beats method,
- The wire and the tuning fork are simultaneously set into vibrations for each vibrating length.
- Beats can be heard when the two frequencies are very close.
- Then, a finer adjustment of the wire is needed so that no beats are heard. This is when the two are in unison.
For the paper-rider method, a small light paper known as the rider R in the form of /\ is placed on the wire at its centre.
- The stem of the vibrating tuning fork is gently pressed on the sonometer box.
- The vibrating length is gradually increased from minimum till the paper rider vibrates and thrown off.
- Because, when the wire resonates with the tuning fork at its lowest fundamental mode, the wire vibrates with maximum amplitude and the centre of the wire is an antinode. Hence, the paper rider is thrown off.
A sonometer is used to determine the frequency of a tuning fork and to verify the laws of vibrating strings.
1) Verification of first law (law of length) of a vibrating string: According to this law, n ∝ 1/L, if T and m are constant. To verify this law, the sonometer wire of given linear density m is kept under constant tension T. The length of the wire is adjusted for the wire to vibrate in unison with tuning forks of different frequencies n1, n2, n3,... . Let L1, L2, L3,….., be the corresponding resonating lengths of the wire. It is found that, within experimental errors, n1L1 = n2L2 =n3L3 = …. . This implies that the product, nL = constant, which verifies the law of length. 2) Verification of second law (Law of tension) of a vibrating string: According to this law, n ∝ , if L and m are constant. To verify this law, the vibrating length L of the sonometer wire of given linear density m is kept constant. A set of tuning forks of different frequencies is used. The tension in the wire is adjusted for the wire to vibrate in unison with tuning forks of different frequencies n1, n2, n3,... ., T1, T2, T3,… be the corresponding tensions. It is found that, within experimental errors, \(\frac{n_1}{\sqrt{T_1}}=\frac{n_2}{\sqrt{T_2}}=\frac{n_3}{\sqrt{T_3}}\)=...... This implies constant which verifies the law of tension. 3) Verification of third law (Law of linear density) of a vibrating string: According to this law, n ∝ \(\sqrt{\frac{1}{m}}\) , if T and L are constant. To verify this law, two wires having different linear densities m1 and m2 are kept under constant tension T. A tuning fork of frequency n is used. The lengths of the wires are adjusted for the wires to vibrate in unison with the tuning fork. Let L1 and L2 be the corresponding resonating lengths of the wires. It is found that, within experimental errors, \(L_1\sqrt{m_1}=L_2\sqrt{m_2}\) This implies \(L\sqrt{m}=\) constant. According to the law of length of a vibrating string, n ∝ 1/L. ∴ n ∝ \(\sqrt{\frac{1}{m}}\) which verifies the law of linear density.
Beats:
This is phenomenon based on the principle of superposition of waves.
When there is superposition of two sound waves, having same amplitude but slightly different frequencies, travelling in the same direction, the intensity of sound varies periodically with time. This phenomenon is known as production of beats.
- If two notes of slightly different frequencies n1 and n2 are played simultaneously, the resulting note from their interference has a frequency of (n1 + n2)/2.
- However, the amplitude of this resulting note varies from the sum to the difference of the amplitudes of the two notes n1 and n2.
- An intensity maximum and an intensity minimum are respectively called waxing and waning.
- Thus, the resulting note will be heard as one of periodic loud (waxing) and faint (waning) sound.
- One waxing and one waning form one beat.
- Formation of beats is an example of interference in time.
The time interval between successive maxima or minima of sound at a given place is called the period of beats.
The number of beats produced per unit time is culled the beat frequency.
Analytical method to determine beat frequency: Consider two sound waves of equal amplitude (A) and slightly different frequencies n1 and n2 (with n1 > n2) propagating through the medium in the same direction and along the same line. These waves can be represented by the equations y1 = A sin 2πn1t and y2 = A sin 2πn2t at x = 0, where y denotes the displacement of the particle of the medium from its mean position. By the principle of superposition of waves, the resultant displacement of the particle of the medium at the point at which the two waves arrive simultaneously is the algebraic sum y = y1 + y2 = A sin 2πn1t + A sin 2πn2t [By using formula, sin C + sin D = 2 sin \((\frac{C+D}{2})\) cos \((\frac{C-D}{2})\) ] ∴ y = 2A sin \([2π(\frac{n_1+n_2}{2})t]\) × cos \([2π(\frac{n_1-n_2}{2})t]\) = 2A cos \([2π(\frac{n_1-n_2}{2})t]\) × sin \([2π(\frac{n_1+n_2}{2})t]\) Let R = 2A cos \([2π(\frac{n_1-n_2}{2})t]\) and n = \(\frac{n_1+n_2}{2}\) ∴ y = R sin 2πnt The above equation shows that the resultant motion has amplitude |R| which changes periodically with time. The period of beats is the period of waxing (maximum intensity of sound) or the period of waning (minimum intensity of sound). The intensity of sound is directly proportional to the square of the amplitude of the wave. It is maximum (waxing) when R becomes maximum. R = ± 2A. ∴ cos \([2π(\frac{n_1-n_2}{2})t]\) = ±1 ∴ \(2π(\frac{n_1-n_2}{2})t\) = 0, p, 2p, 3p …. ∴ t = 0, \(\frac{1}{n_1-n_2}\), \(\frac{2}{n_1-n_2}\), \(\frac{3}{n_1-n_2}\) …. (1) Period of beats = period of waxing = \(\frac{1}{n_1-n_2}\) ∴ Beat frequency = 1/(period of beats) = n1−n2 The intensity of sound is minimum (waning) when R = 0. ∴ cos \([2π(\frac{n_1-n_2}{2})t]\) = 0 ∴ \(2π(\frac{n_1-n_2}{2})t\) = \(\frac{π}{2}\), \(\frac{3π}{2}\), \(\frac{5π}{2}\),…. ∴ t = \(\frac{1}{2(n_1-n_2)}\), \(\frac{3}{2(n_1-n_2)}\), \(\frac{5}{2(n_1-n_2)}\) …. (2) Period of beats = period of waning = \(\frac{1}{n_1-n_2}\) ∴ Beat frequency = 1/(period of beats) = n1−n2 From Eqs. (1) and (2), it can be seen that the waxing and waning occur alternately and with the same period.
Conditions for hearing beats :
For two sound waves to interfere and give rise to beats,
- they should travel in the same medium and arrive at the listener at the same time their frequencies should not differ by more than about 7 Hz for distinct beats
- their amplitudes should be equal or nearly so.
Applications of beats : 1] The phenomenon of beats is used for matching the frequencies of different musical instruments by artists. 2] The speed of an airplane can be determined by using Doppler RADAR. 3] Unknown frequency of a sound note can be determined by using the phenomenon of beats.
Characteristics of Sound : Loudness :The loudness of a note is the magnitude of the sensation produced by the sound waves on the ear. Pitch : By pitch we mean whether the note is high or low. Quality : By quality or timbre is meant that characteristic of a sound by which it is possible to distinguish it from all other sounds of the same pitch and loudness.
Remember : A pure note, consisting of only one frequency, is different from a musical note, which may be a combination of many different frequencies. A musical note has a fundamental, or lowest frequency, and superimposed on it are higher frequencies, called overtones or partials. The number and relative strengths of the partials present determines the timbre of the note. The ear always recognizes the fundamental as determining the pitch of the note.
Intensity of sound : The intensity of sound at a point is the time rate of flow of sound energy passing normally through a unit area at that point.
- SI unit : the joule per second square metre (j/s-m2) or watt per square metre (W/m2).
Factors affecting the loudness of sound : Intensity and loudness are related, but not the same. Intensity is a measurable quantity whereas loudness is a sensation which is not measurable. Loudness depends on the intensity of sound as well as the sensitivity of the ear of the listener.
Decibel : The intensity level of a sound wave, by definition, is
β = log10\((\frac{I}{I_0})\) bels = 10log10\((\frac{I}{I_0})\) decibels as one decibel is 0.1 bel.
- Here, Io (reference intensity) is taken as 10 −12 W/m2.
- Intensity level is expressed in decibel (dB). There is no direct relation between loudness and intensity.
The decibel is not a unit of loudness.
Difference between a musical sound and a noise : Note : If the vibrations are regular the sound is musical, is not always true. For example, a ticking clock does not produce a musical note, or the definite note produced by a card held against the teeth of a rotating toothed wheel is far from being pleasant to hear.
Musical sound
Noise
A musical sound is pleasing to the listener.
Noise is not pleasing to the listener.
The pleasure derived from a musical note is because it strikes the ear as a perfectly undisturbed, uniform sound which remains unaltered as long as it exists.
Noise is accompanied by a rapid, irregular but distinct, alternations of various kinds of sounds.
A musical sound thus has a regularity or smoothness because the vibrations that cause the sound are periodic.
Noise results from discontinuous sudden and sharp sounds with no marked periodicity.
Musical scale (diatonic scale) :
A sequence of frequencies which have a specific relationship with each other is called a musical scale.
A musical scale is constructed on the basis of certain groups of notes with simple intervals.
- A major chord or triad is a group of three notes with frequencies in the ratio 4 : 5 : 6 that produce a very pleasing effect when sounded together.
- The diatonic musical scale is composed of three sets of triads making eight notes.
- Some note called the tonic, is chosen as the basis of the scale, and a triad is constructed using this note as the one of lowest frequency.
- Calling the tonic as the 1st, the major chords are 1st, 3rd and 5th, 4th, 6th and 8th, and 5th, 7th and 9th; 8th and 9th are respectively the octaves of the 1st and 2nd.
- In addition to the eight notes of an octave, that form the major scale, five additional notes are also used. These are derived either by raising or lowering the pitch by the interval 25 / 24. If the pitch is raised the note is sharp, and when lowered, it is flat.
Indian musical scale : Indian music is chiefly based on melody, i.e., consonant notes in suitable succession. Besides this 7 physiological sensation, there is a deep psychological involvement. However, the whole structure of Indian music is based on ragas, which are well-established melody types with a wide variety of emotional content. They can be courageous, amorous, melancholy, cheerful, soothing, or ecstatic. Ragas are capable of conveying these emotions to the listener and different ragas are assigned to different seasons and different parts of the day.
Musical instruments : Musical instruments have been classified in various ways. One ancient system that was based on the primary vibrating medium distinguished three main types of instruments : stringed, wind and percussion.
Stringed instruments (stretched strings) : Wind instruments : Percussion instruments :
Q. The notes of a sitar and a guitar sound different even if they have the same loudness and the pitch. Give reasons.
The quality or timbre of the sound of a sitar is different from that of a guitar. The number of overtones or partials present and their relative intensities determine the quality or timbre of the sound of a musical instrument. Therefore, even if the pitch and the loudness are the same, the notes of a sitar and a guitar sound different.
Download PDF from store : Class-12-Physics-Chapter-6-Superposition of Waves–Text Book Get PDF from store : Class-12-Physics-Chapter-6-Superposition of Waves–Notes Get PDF from store : Class-12-Physics-Chapter-6-Superposition of Waves–Solution
Main Page : – Maharashtra Board Class 12th-Physics – All chapters notes, solutions, videos, test, pdf. Previous Chapter : Chapter-5-Oscillations –Online Solution Next Chapter : Chapter-7- Wave Optics – Online Solution
We reply to valid query.