Notes-Part-2
Topics to be Learn : Part-2
|
Atomic Nucleus:
Constituents of a Nucleus:
- A proton, a positively charged particle, and a neutron, a neutral (uncharged) particle, are the constituents of an atomic nucleus.
- The term nucleon (nuclear constituent) refers to a proton as well as a neutron.
Atomic number : The number of protons in the nucleus of an atom of an element is called the atomic number of the element. It is also known as the proton number.
It is denoted by Z.
Mass number : The number of nucleons (protons and neutrons) in the nucleus of an atom is called the mass number or the atomic mass number. It is denoted by A.
- The number of neutrons in the nucleus of an atom is known as the neutron number, denoted by N. It is usually greater than Z, with die exceptions of helium (2 protons, 2 neutrons) and hydrogen (1 proton, no neutron)
- A = Z + N.
Atomic symbol for an element :
An atom is represented as \(_{Z}^{A}X\) where X is the chemical symbol for the element, Z is the atomic number and A is the mass number.
Examples: Hydrogen \(_{1}^{1}H\), carbon \(_{6}^{12}C\) and oxygen \(_{8}^{16}O\)
Characteristic of the element : The atomic number of an element, which is the number of protons in the nucleus of an atom of the element, is characteristic of the element. The element's chemical properties and position in the current periodic table are determined by its atomic number, which is equal to the number of electrons in an atom.
Isotopes : Atoms of an element having the same atomic number (Z) but different mass numbers (A) are called the isotopes of that element.
Isotopes of an element have different neutron numbers but the same chemical properties.
- Example : Hydrogen nucleus can have zero, one or two neutrons. These varieties of hydrogen are referred as hydrogen (\(_{1}^{1}H\) ), deuterium (\(_{1}^{2}H\) ) and tritium (\(_{1}^{3}H\) ). Deuterium and tritium have one and two neutrons in their nuclei, respectively, in addition to the single proton (Z = 1). I
Isobars : Atoms of different elements that have the same mass number (A) but different atomic numbers (Z) are called isobars.
Although isobars have the same mass number, they are different elements because the chemical nature of an element is determined by its atomic number. Isobars have different neutron numbers.
- Example : \(_{6}^{13}C\) and \(_{7}^{13}N\) are isobars. They have the same mass number, A (viz., 13), but their different proton numbers, Z (6 and 7) make them different elements.
Isotones : Atoms of different elements that have the same neutron number (N) but different atomic numbers (Z) are called isotones.
Although isotones have the same neutron number, they are different elements because the chemical nature of an element is determined by its atomic number.
- Example : \(_{14}^{31}Si\) and \(_{15}^{32}P\) are isotones. The neutron number of is N = 31 − 14 = 17, the same as that of (N = 32 − 15 = 17). But their different proton numbers, Z (14 and 15, respectively) make them different elements.
Units for measuring masses of atoms and subatomic particles :
Masses of atoms and subatomic particles are measured in three different units. First unit is the usual unit kg. But kg is not a convenient unit to measure masses of atoms or subatomic particles which are extremely small compared to one kg. Therefore, another unit called the unified atomic mass unit (u) is used for the purpose.
Unified atomic mass unit (u) :
The unified atomic mass unit is an accepted but non-SI unit of mass. It is defined to be equal to 1/12 of the mass of a free atom of the isotope of carbon with mass number 12 which is at rest and in its ground state. It is denoted by u.
Its value in SI unit is obtained experimentally.
1 u= 1.660538782 (83) x 10−27 kg, with the standard uncertainty in the last two digits given in parenthesis.
Example : The masses of electron, proton and neutron, me, mp and mn respectively, in kg unit are:
me = 9.109383 × 10−31 kg
mp = 1.672623 × 10−27 kg
mn = 1.674927 × 10−27 kg
Taking, 1 u = 1.660538782 x 10−27 kg
In this unit, the masses of the above three particles are
me = 0.00055 u
mp = 1.007825 u
mn = 1.008665 u.
The third unit for measuring masses of atoms and subatomic particles is in terms of the amount of energy that their masses are equivalent to.
Einstein’s mass-energy relation : A particle having mass m is equivalent to an amount of energy E = mc2.
The unit used to measure masses in terms of their energy equivalent is the eV/c2.
One atomic mass unit is equal to 931.5 MeV/c2.
The masses of the three particles in this unit are
me = 0.511 MeV/c2
mp = 938.28 MeV/c2
mn = 939.57 MeV/c2
| Einstein's mass-energy relation :
On the basis of his theory of relativity, Einstein showed that mass is a form of energy. Mass and energy are interconvertible. When a mass m is converted into energy, the resulting energy is E = mc2, where c is the speed of light in free space. This expression is called Einstein's mass-energy relation. It shows that a very large quantity of energy is obtained even when a very small amount of mass is converted into it. |
Sizes of Nuclei:
The size of an atom is decided by the sizes of the orbits of the electrons in the atom. Larger the number of electrons in an atom, higher are the orbits occupied by them and larger is the size of the atom.
Similarly, all nuclei do not have the same size, the size of a nucleus depends on the number of nucleons present in it, i.e., on its atomic number A.
From experimental observations it has been found that the radius R of a nucleus is related to A.
Nucleus of radius R has a volume \(\frac{4}{3}\)πR3
∴ R3 ∝ A or R ∝ A1/3
∴ R = R0A1/3
where R0 ≈ 1.2 x 10−15m = 1.2 fm
∴ R ≈ 1.2 A1/3 fm
Nuclear density :
Also, it is experimentally found that the volume of a nucleus is directly proportional to the mass number A. As both nuclear mass and volume are proportional to the mass number, nuclear density is essentially the same for all nuclei.
Nuclear volume = \(\frac{4}{3}\)πR03A
∴ Nuclear density, ρ = \(\frac{nuclear\,\,mass}{nuclear\,\,volume}\) = \(\frac{mA}{\frac{4}{3}πR_{0}^{3}A}\) … (1)
Thus, the density of a nucleus does not depend on the atomic number of the nucleus and is the same for all nuclei.
Substituting the value of m (1.660538782 x 10−27 kg), π(3.14) and R0 (1.2 x 10−15m) in Eq. (1), the value of the density is obtained as 2.3 x 1017 kg/m3 which is extremely large.
The order of nuclear density is 1017 kg/m3
Nuclear Forces: Force that determines the structure of the nucleus is called the nuclear force. It is a strong force. This force acts between protons and neutrons and is mostly attractive.
It is different from the electrostatic and gravitational force in terms of its strength and range,
Properties of nuclear force : It can be summarized as follows.
- It is the strongest force among subatomic particles. Its strength is about 50-60 times larger than that of the electrostatic force.
- Unlike the electromagnetic and gravitational forces which act over large distances (their range is infinity), the nuclear force has a range of about a few fm and the force is negligible when two nucleons are separated by larger distances.
- The nuclear force is independent of the charge of the nucleons, i.e., the nuclear force between two neutrons with a given separation is the same as that between two protons or between a neutron and a proton at the same separation.
Stable nuclei : Those nuclei which for certain combinations of neutrons and protons do not spontaneously disintegrate are called stable nuclei.
There are two aspects that decide the stability of a nucleus.
- The existence of nuclear energy levels implies certain configurations to achieve potential energy minimum.
- Balance of forces.
Just like energy levels in atoms, nuclear energy levels are filled in sequence obeying the exclusion principle. Thus, there is a tendency for N to equal Z, or to have both even Z and even N.
Mass defect : The difference between the sum of the masses of all the individual nucleons in a nucleus and the mass of the nucleus is known as the mass defect.
Mass defect, Δm = (Zmp + Nmn) − M
where mp = proton mass, mn = neutron mass, M = mass of the nucleus, Z = atomic number and N = A − Z is the neutron number.
Nuclear Binding Energy:
In the atomic nucleus, the protons and the neutrons are bound together by a strong, short range and charge independent, attractive force called the nuclear force. It is necessary to supply energy to break the nucleus. The minimum energy required to separate a nucleus into its free constituents, i.e protons and neutrons, is known as the nuclear binding energy. It is the mass energy of the nucleons minus the mass energy of the nucleus.
From Einstein's mass-energy relation,
Nuclear binding energy = Δmc2
= [(Zmp + Nmn) – M]c2 (in joule)
= [(Zmp + Nmn) – M]\(\frac{c^2}{e}\) (in eV)
where c is the speed of light in free space and e is the elementary charge. In calculations using the above equations, mp is replaced by mH (mass of hydrogen atom). M is taken to be the atomic mass and not nuclear mass because the electron masses cancel out and the difference in electronic binding energies can be ignored as these are 106 times smaller than the nuclear binding energy.
∴ Nuclear binding energy = [(ZmH + Nmn) – Matom]c2 (in joule)
The minimum energy required on the average to separate a nucleon from a given nucleus is called the binding energy per nucleon for that nucleus. It is the nuclear binding energy for a nucleus divided by its mass number.
∴ Binding energy per nucleon = Δmc2/A = [(Zmp + Nmn) – M]\(\frac{c^2}{e}\)
Significance of binding energy per nucleon :
The greater the binding energy per nucleon in a nucleus, the greater is the minimum energy needed to remove a nucleon from the nucleus. Thus, binding energy per nucleon indicates the stability of a nucleus.
| Know This : The binding energy per nucleon is high when both Z and N are even numbers, and such nuclei are most common. Nuclei with both Z and N odd are very rare. |
Binding energy per nucleon as a function of mass number :
Figure shows the plot of the binding energy per nucleon (BE/A, in MeV per nucleon) against mass number A.
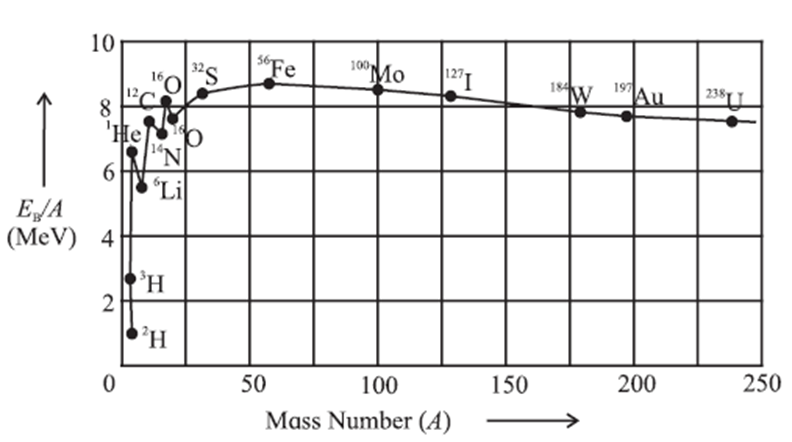
From above Fig. we can draw the following inferences :
(i) The greater the binding energy per nucleon the more Stable is the nucleus because greater is the minimum energy needed to remove a nucleon. Thus, the nuclei appearing high on the plot are more tightly bound.
(ii) BE/ A has a maximum value of about 8.8 MeV per nucleon at A = 56 (56Fe nuclide) and then decreases to 7.6 MeV per nucleon at A = 238 (238U nuclide).
Thus, the iron nuclide 56Fe has the maximum binding energy per nucleon and is the most stable nuclide. Also, the peak at A = 4 shows that the 4Henucleus (α-particle) has higher binding energy per nucleon compared to its neighbours in the periodic table and is exceptionally stable.
(iii) The increase in BE/A as A decreases from 240 to 60 shows that if a heavy nucleus splits into two medium-sized fragments, each of the new nuclei will have more BE/A than the original nucleus. The binding energy difference, which can be very large, will then be released. The process of splitting a heavy nucleus is called nuclear fission. The energy released in a fission of 235U nucleus is about 200 MeV.
(iv) Joining together, or fusing, two very light nuclei to form a single nucleus will also lead to larger BE/A in the new heavier nucleus. Again, the binding energy difference will be released. This process, which is called nuclear fusion, is also a very effective way of obtaining energy.
Radioactive Decays:
Radioactivity is the phenomenon in which unstable nuclei of an element spontaneously distintegrate into nuclei of another element by emitting α or
β particles accompanied by y-rays (gamma rays). Such transformation is known as radioactive transformation or radioactive decay.
Discovery of radioactivity :
Antoine Henri Becquerel (1852-1908), French physicist, discovered radioactivity in 1896. He had kept photographic plates wrapped in a thick black paper in a drawer of his desk. Later, he also kept uranium salts near the photographic plates. After some days he developed the photographic plates and was surprised to find that they were fogged although he had protected them from light. Becquerel concluded that uranium salts must be emitting some invisible rays which affected the photographic plates. In this way, radioactivity was discovered by Becquerel.
Radioactive element : The element which exhibits the property of radioactivity, i.e., spontaneous disintegration of unstable nuclei of the element by emission of α or β particles accompanied by γ-rays (gamma rays) is called a radioactive element.
Examples :Uranium, thorium, polonium, radium, actinium.
Radioactive decay processes :
Radioactive decays occur because the parent nuclei are unstable and get converted to more stable daughter nuclei by the emission of some particles.
The processes by which a radioactive element can decay are :
- α -decay, by emission of an α -particle ( \(_{2}^{4}He\) nucleus),
- β —decay, by emission of an electron ( \(_{-1}^{\,0}e\) ) or a positron (\(_{1}^{\,0}e\)), and
- γ-decay by emitting electromagnetic radiations (γ -rays) of very short wavelength of about 10−12 m to 10−14 m.
Q factor of the decay : In a radioactive decay, the difference in the energy equivalent of the mass of the parent atom and that of the sum of the masses of the products is called the Q value or Q factor of the decay. It is also called disintegration energy.
(i) α -decay : A radioactive transformation in which an α –particle is emitted is called α-decay. In an α—decay, the atomic number of the nucleus decreases by 2 and the mass number decreases by 4.
Formula for the energies generated :
\(_{Z}^{A}X→_{2}^{4}α+_{Z-2}^{A-4}Y\) + energy released
Example :
Q = [mU − mTh − mα]c2
(ii) β-decay : A radioactive transformation in which a β –particle is emitted is called β-decay. In a β-decay, the atomic number of the nucleus increases by 1 and the mass number remains unchanged.
Formula for the energies generated :
\(_{Z}^{A}X→_{-1}^{\,0}β+_{Z+1}^{A}Y\) + energy released
Example :
where is the antineutrino emitted to conserve the momentum, energy and spin.
Q = [mTh − mPa − me]c2
In a β+—decay, the atomic number of the nucleus decreases by 1 and the mass number remains unchanged.
Example :
where ve is the neutrino emitted to conserve the momentum, energy and spin.
Q = [mP − mSi − me]c2
(iii) γ-decay :
A given nucleus does not emit α- and β –particles simultaneously. However, on emission of α or β -particles, most nuclei are left in an excited state.
A nucleus in an excited state emits a γ-ray photon in a transition to the lower energy state. Hence, α- and β —particle emissions are often accompanied by γ -rays.
Formula for the energies generated in γ-decay :
\(_{Z}^{A}X^*→_{0}^{0}γ+_{Z}^{A}X\)(energy released is carried by the γ –ray photon)
Radioactivity is a nuclear phenomenon :
The rate of disintegration of a radioactive material is not affected by changes in physical and chemical conditions such as
- Temperature and pressure
- Action of electric and magnetic fields
- Chemical composition of the material.
The above changes affect the orbital electrons, but not the nucleus.
Therefore, we conclude that radioactivity is a nuclear phenomenon.
Nature and properties of α-particles :
Nature of α -particles :
- An alpha particle is a helium nucleus, i.e., a doubly ionized helium atom. It consists of two protons and two neutrons.
- Mass of the α-particle ≈ 4 u. Charge on the α —particle = 2 x charge on the proton
Properties of α -particles :
- Of the three types of radioactive radiations, α-particles have the maximum ionizing power. It is about 100 times that of β-particles and 104 times that of γ-rays.
- They have the least penetrating power, about 100 times less than that of β -particles and 104 times less than that of γ—rays. They can pass through very thin sheets of paper but are scattered by metal foils and mica. Since α -particles produce intense ionization in a medium, they lose their kinetic energy quickly. As a result, they do not penetrate more than a few centimetres (about 2.7 cm to 8.6 cm) in air under normal conditions.
- They are deflected by electric and magnetic fields since they are charged particles. Their deflection is less than that of β -particles in the same field.
- They affect photographic plates.
- They cause fluorescence in fluorescent materials such as zinc sulphide.
- They emerge from the nuclei with tremendous speeds in the range of \(\frac{1}{100}\)th to \(\frac{1}{10}\)th of the speed of light in free space.
- They destroy living cells.
Nature and properties of β-particles :
Nature of β-particles : A β—particle is an electron or a positron.
Properties of β -particles :
- β -particles have a moderate ionizing power. It is about 100 times less than that of alpha-particles, but 100 times more than that of γ-rays.
- They have a moderate penetrating power. It is about 100 times more than that of alpha -particles, but 100 times less than that of γ -rays.
- They are deflected by electric and magnetic fields.
- Their deflection is more than the deflection of alpha-particles in the same field but in the opposite direction.
- They affect photographic plates.
- They cause fluorescence in a fluorescent material such as zinc sulphide.
- Their energies and speeds are very high. Their speed is of the order of 108 m/s. Some β –particles have speeds of the order of 0.99 c, where c is the speed of light in free space.
- They cause more biological damage than α-particles, because they have more penetrating power.
Nature and properties of γ-particles :
Nature of γ-particles :
- γ—rays are electromagnetic waves of very short wavelength (about 10−12 m to 10−14 m).
- They are uncharged.
Properties of γ-rays :
- γ-rays produce feeble ionization. Their ionizing power is 104 times less than that of at-particles and 100 times less than that of β —particles.
- They have the maximum penetrating power. It is about 100 times that of β-particles and 104 times that of α —particles.
- They are not deflected by electric and magnetic fields as they are uncharged.
- They affect photographic plates.
- They cause fluorescence in a fluorescent material such as zinc sulphide.
- Their speed in free space is 3 x 108 m/s (the same as that of light waves and X-rays in free space).
- γ -rays can be diffracted by crystals. In recent times, γ-ray diffraction has emerged as a powerful tool in structural and defect studies of crystals.
- They destroy living cells and tissues and are used for destroying cancer cells.
Law of Radioactive Decay:
Law of radioactive decay : At any instant, the rate of radioactive disintegration is directly proportional to the number of nuclei of the radioactive element present at that instant.
Derivation : Let N0 be the number of nuclei present at time t = 0, and N the number of nuclei present at time t.
From the law of radioactive decay, dN/dt ∝ N
∴ dN/dt = −λN …(1)
which is the differential form of the law.
∴ dN/N = −λdt …(2)
where λ is a constant of proportionality called the radioactive decay constant or the disintegration constant. It is a constant for a particular radioactive element. The minus sign indicates that N decreases as t increases.
Integrating Eq. (1),
\(\int_{N_0}^{N}\frac{dN}{N}=-\int_{0}^{t}λdt=-λ\int_{0}^{t}dt\)
∴ loge N – loge N0 = −λt
∴ loge (N/N0) = −λt …(3)
∴ N/N0 = e−λt
∴ N = N0 e−λt ..( This equation is also written in the form N(t) = N0 e−λt )
This is the exponential form of the law of radioactive decay. It shows that the number of nuclei present decreases exponentially with time.
Activity of a sample of radioactive element :
The rate of disintegration of a sample of a radioactive element is called its activity. Let A denote the activity at time t and A0 the initial activity. Then,
A = |dN/dt| = λN
Now, A0 = λN0 and N = N0 e−λt
∴ A = λN = λN0 e−λt = A0 e−λt …..(1) [..This is also written in the form A(t) = A0e−λt]
∴ e−λt = A/A0
∴ λt = loge (A/A0) =2.303 log10 (A/A0)
∴ λ = \(\frac{2.303}{t}\)log10 (A/A0) ….(2)
The SI unit of activity is called the becquerel (Bq) in honour of Henri Becquerel.
1 Bq = 1 disintegration per second.
The earlier unit, the curie (Ci) was based on the activity of 1 gram of 226Ra.
1 Ci = 3.7 x 1010 Bq. It was named after Marie Curie, Polish-born French chemist.
Half-life of Radioactive Material:
Half-life a radioactive element : The half-life of a radioactive element is defined as the average time interval during which half of the initial number of nuclei of the element disintegrate.
Relation between half-life and decay constant :
Let N0 be the number of nuclei of a radioactive element present at time t= 0 and N, the number of nuclei present at time t. From the law of radioactive decay,
N = N0 e−λt
where λ is the decay constant of the element.
If T is the half-life of the element, then, N = N0/2
when t = T.
∴ N0/2 = N0 e−λT
∴ 1/2 = e−λT
∴ 2 = eλT
∴ loge 2 = λT
∴ T = loge 2/λ = \(\frac{2.303log_{10}2}{λ}\) = \(\frac{2.303×0.3010}{λ}\)
∴ T = 0.693/λ
This is the relation between the half-life and the decay constant of a radioactive element.
Remember : Radioactive decay law is statistical in nature and applicable only when the number of nuclei in the sample under consideration is very large. λ gives the probability that a nucleus of the element will decay in one second. We cannot know the exact number of nuclei that would decay in a given time interval. Hence, the use of the term average in the definition of half-time.
Average Life of a Radioactive Species:
Let N0 = number of nuclei present at time t = 0 and λ = decay constant of a radioactive species.
|dN| = | λNdt l.
∴ The number of nuclei decaying between time t and t + dt is λ N0 e−λt dt.
The life time of these nuclei is t. The average life or mean life of a radioactive species is denoted by τ and is, by definition,
τ = \(\frac{1}{N_0}\int_{0}^{∞}tλN_0e^{-λt}dt\)=\(λ\int_{0}^{∞}te^{-λt}dt\)=\(\frac{1}{λ}\)
Now T1/2 = 0.693/λ
∴ τ = T1/2/0.693
Nuclear Energy:
Nuclear energy is the energy released during a nuclear reaction, such as nuclear fusion, nuclear fission, or the interaction of two nuclei.
- Nuclear reactions release energy on the scale of a few MeV, while chemical reactions produce energy on the order of a few eV per reaction. Therefore, the nuclear energy released is around a million times greater than the chemical energy released for the same weight of fuel.
Nuclear reaction : A reaction between the nucleus of an atom and a bombarding particle leading to the production of a new nucleus and, in general, the ejection of one or more particles is known as a nuclear reaction.
Example : \(_{2}^{4}α+_{13}^{27}Al→_{15}^{30}P+_{0}^{1}n\)+ Q
Here, is the bombarding particle, is the target nucleus, is the product nucleus and and is the ejected particle. Q is the energy released in the reaction. It is carried (usually) by the ejected particle.
The total momentum, energy, spin, charge and number of nucleons are conserved in a nuclear reaction.
Nuclear fission : It is a nuclear reaction in which a heavy nucleus of an atom, such as that of uranium, splits into two or more fragments of comparable size, either spontaneously or as a result of bombardment of a neutron on the nucleus (induced fission).
It is followed by emission of two or three neutrons.
The mass of the original nucleus is more than the sum of the masses of the fragments. This mass difference is released as energy, which can be enormous as in the fission of 235U.
Nuclear fission was discovered by Lise Meitner, Otto Frisch, Otto Hahn and Fritz Strassmann in 1938.
Fission of uranium-235 :
The products of the fission of 235U by thermal neutrons are not unique. A variety of fission fragments are produced with mass number A ranging from about 72 to about 138, subject to the conservation of mass-energy, momentum, number of protons (Z) and number of neutrons (N).
A few typical fission equations are :
(1) \(_{92}^{235}U+_{0}^{1}n→_{92}^{236}U→_{54}^{140}Xe+_{38}^{94}Sr+2_{0}^{1}n\) + 200 MeV
(235 + 1 = 236 = 140 + 94 + 2)
(2) \(_{92}^{235}U+_{0}^{1}n→_{92}^{236}U→_{56}^{144}Ba+_{36}^{90}Kr+2_{0}^{1}n\) +200 MeV
(235 + 1 = 236 = 144 + 90 + 2)
(3) \(_{92}^{235}U+_{0}^{1}n→_{92}^{236}U→_{57}^{148}La+_{35}^{85}Br+3_{0}^{1}n\) +200 MeV
(235 + 1 = 236 = 148 + 85 + 3) .
Application of Nuclear fission :
Nuclear fission is used in (1) a nuclear reactor as very efficient and the least polluting source of energy to generate electricity (2) atomic bombs.
Uranium Nuclear Reactor:
A nuclear reactor is a device in which a nuclear fission chain reaction is used in a controlled manner
- To produce energy in form of heat which is then converted into electricity or
- To produce radioisotopes or
- To produce new nuclides using a suitable fissionable material such as uranium or plutonium.
In a uranium reactor is bombarded by slow neutrons to produce which undergoes fission.
Principles of a nuclear reactor : In a nuclear reactor fuel rods are used to provide a suitable fissionable material such as . Control rods are used to start or stop the reactor. Moderators are used to slow down the fast neutrons ejected in a nuclear fission to the appropriate lower speeds. Material used as a coolant removes the energy released in the nuclear reaction by converting it into thermal energy for production of electricity.
A chain reaction is a self-multiplying process in which neutrons ejected in a nuclear fission strike neighbouring nuclei of fissionable material and cause more fissions.
A fission of nucleus by a thermal neutron leads to ejection of two or three neutrons (2.7 neutrons on an average) having high kinetic energy of about 2 MeV. The kinetic energy of at least one of these neutrons is lowered to about 0.025 eV by a suitable moderator and the neutron is used to cause further fission. The process continues and hence it is called a chain reaction.
Difference between a nuclear reactor and a nuclear bomb :
In a nuclear reactor, a nuclear fission chain reaction is used in a controlled manner, while in a nuclear bomb, the nuclear fission chain reaction is not controlled, releasing tremendous energy in a very short time interval.
Nuclear fusion : A type of nuclear reaction in which lighter atomic nuclei (of low atomic number) fuse to form a heavier nucleus (of higher atomic number) with the release of enormous amount of energy is called nuclear fusion.
Very high temperatures, of about 107 K to 108 K, are required to carry out nuclear fusion. Hence, such a reaction is also called a thermonuclear reaction.
Example ;The D-T reaction, being used in experimental fusion reactors, fuses a deuteron and a triton nuclei at temperatures of about 108 K.
\(_{1}^{2}D+_{1}^{3}T→_{2}^{4}He+_{0}^{1}n\)+ 17.6 MeV
(deuteron + triton → Helium nucleus + neutron)
Application of Nuclear fusion :
- Nuclear fusion is used in (experimental) fusion reactors to generate electricity without the hazards of radioactive radiations and radioactive pollution which happens with fission reactors.
- Nuclear fusion reactions in the interior of stars are the source of their energy output and the means of synthesis of higher elements like carbon, nitrogen and silicon from hydrogen and helium.
Nuclear fusion in stars :
Nuclear fusion is taking place all the time in the universe. It mostly takes place at the centres of stars where the temperatures are high enough for nuclear reactions to take place.
Basic exothermic reaction in stars :
The fusion of hydrogen nuclei into helium nuclei results in release of energy. It is the basic exothermic reaction in stars.
(1) The proton—proton cycle :
\(_{1}^{1}H+_{1}^{1}H→_{1}^{2}H+e^+v\) …. (1)
\(_{1}^{1}H+_{1}^{2}H→_{2}^{3}He+γ\) …. (2)
\(_{2}^{3}He+_{2}^{3}He→_{2}^{4}He+_{1}^{1}H+_{1}^{1}H\)
The total energy released (Δmc2) is 24,7 MeV_
(2) The carbon cycle :
\(_{1}^{1}H+_{6}^{12}C→_{7}^{13}N\)
\(_{7}^{13}N→_{6}^{13}C+e^++v\)
\(_{1}^{1}H+_{6}^{13}C→_{7}^{14}N+γ\)
\(_{1}^{1}H+_{7}^{14}N→_{8}^{15}O+γ\)
\(_{8}^{15}O→_{7}^{15}N+e^++v\)
\(_{1}^{1}H+_{7}^{15}N→_{6}^{12}C+_{2}^{4}He\)
The total energy released is 24.7 MeV
| Know This :
The fusion inside stars can only take place between nuclei having mass number smaller than that of iron, i.e., 56. The reason for this is that iron has the highest EB/A value among all elements. If an iron nucleus fuses into another nucleus, the atomic number of the resulting nucleus will be higher than that of iron and hence it will have smaller EB/A. The mass of the resultant nucleus will hence be larger than the sum of masses of the reactants and energy will have to be supplied to the reactants for the reaction to take place. The elements heavier than iron which are present in the universe are produced via other type of nuclear reaction which take place during stellar explosions. |
We reply to valid query.