Electrochemistry
Maharashtra Board-Class-12-Chemistry-Chapter-5
Notes-Part-2
Topics to be Learn : Part-2
|
Electrochemical cells :
Electrochemical cell : It is made up of two electronic conductors, such as metal plates, that are immersed in an electrolytic or ionic conductor, such as an aqueous electrolytic solution or a pure liquid of a molten electrolyte.
Electrochemical reactions :
- The Chemical reactions occurring in electrochemical cells which involve transfer of electrons from one species to other are called electrochemical reactions. They are redox reactions.
- These reactions are made of two half reactions namely oxidation at one electrode (anode) and reduction at another electrode (cathode) of the electrochemical cell.
- The net cell reaction is the sum of these half reactions.
Electrodes : Electrodes are the surfaces on which oxidation and reduction half reactions take place.
- The electrodes which take part in the reactions are called active electrodes while those which do not take part in the reactions are called inert electrodes.
- Cathode : It is an electrode at which the reduction takes place. At this electrode the species undergoing reduction gains electrons.
- Anode : It is an electrode at which oxidation takes place. At this electrode, the species undergoing oxidation loses electrons.
Types of electrochemical cells : There are two types of electrochemical cells.
(i) Electrolytic cell : An electrolytic cell is an electrochemical cell in which a non-spontaneous chemical reaction is forced to occur by passing direct electric current into the solution from an external source and electrical energy is converted into chemical energy.
- E.g. voltameter, electrolytic cell for deposition of a metal.
(ii) Voltaic or galvanic cell : A voltaic cell or galvanic cell is an electrochemical cell in which a spontaneous chemical reaction produces electricity and chemical energy is converted into electrical energy.
- E.g. Daniell cell, dry cell, lead storage battery, fuel cells, etc.
Construction of Electrolytic cell :
- Electrolytic cell consists of a container in which electrolyte is placed. Two electrodes are immersed in the electrolyte and connected to a source of direct current.
- At anode (+) a species oxidises with the removal of electrons. These electrons are pulled from anode and pushed to cathode through an external circuit. The electrons are supplied to species at cathode which are reduced.
Electrolysis : Electrolysis is the process of converting electrical energy into chemical energy through the non-spontaneous chemical decomposition of an electrolyte by the passage of an electric current through its aqueous solution or fused mass. E. g. Electrolysis of fused NaCl.
Electrolysis of molten NaCl :
(1) Construction of cell : The electrolytic cell consists of a container in which fused NaCl is placed. Two graphite electrodes are immersed in it. They are connected by metallic wires to a source of direct current that is battery. This is shown in fig.
The carbon electrode connected to terminal electrode of the battery is anode and that connected to negative terminal of the battery is cathode.
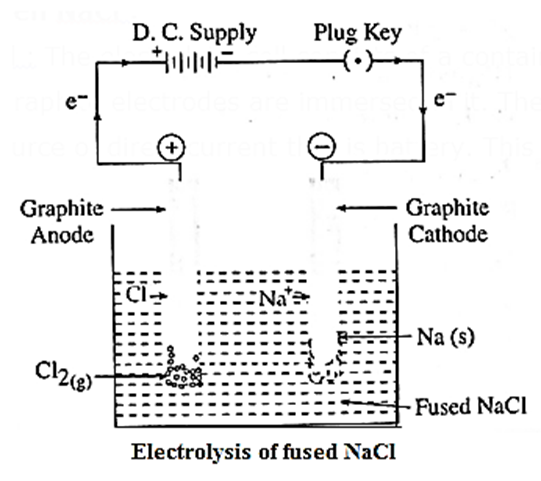
(2) Working of the cell :
(A) In the external circuit, the electrons flow through the wires from anode to cathode of the cell.
(B) The fused NaCl dissociates to form cations (Na+) nd anions (Cl“).
NaCl(fused) → Na+(l) + Cl−(l)
Na+ migrate towards cathode and Cl− migrate towards anode.
(3) Reactions in electrolytic cell :
Reduction half reaction at cathode : The Na+ ions get reduced by accepting electrons from a cathode supplied by a battery and form metallic sodium.
Na+(l) + e− → Na(s) (reduction)
Oxidation half reaction at anode : The Cl− ions gel oxidised by giving up electrons to the anode forming neutral Cl atoms in the primary process, and these Cl atoms combine forming Cl2 gas in the secondary process.
2Cl− → Cl(g) + Cl(g) + 2e− ..(Primary oxidation half reaction)
2Cl(g) → Cl2(g) …..(Secondary process)
---------------------------
2Cl → Cl2(g) + 2e− …..(Overall oxidation at anode)
The released electrons in the anodic oxidation half reaction return to battery through the metallic wires.
Net cell reaction : In order to maintain the electrical neutrality, the number of electrons gained at cathode must be equal to the number of electrons released at anode. Hence the reduction half reaction is multiplied by 2 and both reactions, oxidation half reaction and reduction half reaction are added to obtain a net cell reaction.
2Na+(l) + 2e− → 2Na(s) (Reduction half reaction)
2Cl (l) → Cl2(g) + 2e− (Oxidation half reaction)
---------------------------
2Na+(l) + 2Cl−(l) → 2Na(s) + Cl2(g) (Overall reaction)
(4) Results of electrolysis :
- A molten silvery white Na is formed at cathode which floats on the surface of molten NaCl.
- A pale green Cl2 gas is liberated at anode.
Decomposition of NaCl into metallic sodium and Cl2(g) is nonspontaneous. The electrical energy supplied by the battery forces the reaction to occur.
Electrolysis of aqueous NaCl :
(1) Construction of an electrolytic cell : It consists of a vessel containing a NaCl aqueous solution. Two inert electrodes (graphite electrodes) are immersed in it and connected to an external power source, such as a battery. The electrode connected to the negative terminal is referred to as a cathode, while the electrode connected to the positive terminal is referred to as an anode.

(2) Working of the cell :
NaCl(aq) and H2O(l) dissociate as follows
NaCl(aq) → Na+(aq) + Cl−(aq)
H2O(l) → H+(aq) + OH−(aq) (Partially)
(3) Reactions in electrolytic cell :
Reduction half reaction at cathode : There are Na+ and H+ ions but since H+ are more reducible than Na+ they undergo reduction liberating hydrogen and Na+ are left in the solution.
2H2O(l) + 2e− → H2(g) + 2OH−(aq) (reduction) E0 = − 0.83 V
Oxidation half reaction at anode : At anode there are Cl− and OH−. But Cl− ions are preferably oxidised due to less decomposition potential.
2Cl−(aq) → 2Cl(g) + 2e−
2Cl(g) → Cl2(g)
-----------------------------------
2Cl−(g) → Cl2(g) + 2e− (overall reaction) E0 = − 1.36 V
Net cell reaction : Since two electrons are gained at cathode and two electrons are released at anode for each redox step, the electrical neutrality is maintained. Hence we can write,
H2O(l) + 2e− → H2(g) + 2OH−(aq) (cathodic reduction)
2Cl−(g) → Cl2(g) + 2e− (anodic oxidation)
--------------------------------------------
2H2O(l) + 2Cl−(aq) → H2(g) + 2OH−(aq) + Cl2(g) (overall reaction)
Since Na+ and OH− are left in the solution, they form NaOH(aq).
(4) Results of electrolysis :
- H2 gas is liberated at cathode.
- Cl2 gas is liberated at anode.
- NaOH is formed in the solution and it reacts basic.
Know This :
|
Quantitative aspects of electrolysis :
Knowing the stoichiometry of the half reaction at the electrode allows you to calculate the mass of reactant consumed or the mass of product formed at an electrode during electrolysis.
(i) Calculation of quantity of electricity : If an electric current of strength I(A) is passed through the cell for t seconds, then quantity of electricity (Q) obtained is given by,
Q = I x t C(Coulomb)
(ii) Calculation of moles of electrons passed : The charge carried by one mole of electrons is referred to as one faraday (F). If total charge passed is Q(C), then
Moles of electrons passed = \(\frac{Q(C)}{F(C/mol)}\)
The charge of one mole electrons is 96500 coulombs (C). It is referred to as one faraday (1F). Hence,
Moles of electrons actually passed = \(\frac{Q(C)}{96500(C/mol)}\)
(iii) Calculation of moles of product formed : Consider one mole of ions, Mn+(aq) which will require n moles of electrons for reduction.
Mn+(aq) + ne− → M (Reduction half reaction)
∴ Mole ratio = \(\frac{\text{moles of product formed in the half reaction}}{\text{moles of electrons required in the half reaction}}\)
∴ Moles of product formed = moles of electrons passed x mole ratio
= \(\frac{Q}{96500}\) x mole ratio
= \(\frac{l×t}{96500}\) x mole ratio
(iv) Calculation of mass of product : Mass, W of product formed is given by.
W = moles of product x molar mass of product (M)
= \(\frac{Q}{96500}\) x mole ratio x M
= \(\frac{l×t}{96500}\) x mole ratio x M
When two electrolytic cells containing different electrolytes are connected in series so that same quantity of electricity is passed through them, then the masses W1 and W2 of products produced are given by,
W1 = \(\frac{Q}{96500}\) x (mole ratio)1 x M1
W2 = \(\frac{Q}{96500}\) x (mole ratio)2 x M2
∴ W2/W1 = \(\frac{(\text{mole ratio})_2×M_2}{(\text{mole ratio})_1×M_1}\)
∴ \(\frac{(\text{mole ratio})_2}{(\text{mole ratio})_1}\) = \(\frac{W_2}{W_1}×\frac{M_1}{M_2}\) = \(\frac{W_2/M_2}{W_1/M_1}\)
= \(\frac{n_2}{n_1}\)
Galvanic or voltaic cell :
Galvanic or voltaic cell : Galvanic or voltaic cells (electrochemical cell), is a device that generates electrical energy through a spontaneous chemical reaction inside it. Chemical energy is converted into electrical energy in this process.
- A galvanic (or voltaic) cell is made of two half cells.
- Example : Daniell cell.
Half cell or Electrode : It is a metal electrode dipped in the electrolytic solution and-capable of establishing oxidation reduction equilibrium with one of the ions of electrolyte solution and develop electrode potential. E.g. Zn in ZnSO4 solution.
Salt bridge :
A salt bridge is a U-shaped glass tube containing a saturated solution of a strong electrolyte, like KCl, NH4NO3, Na2SO4 in a solidified agar-agar gel.
A hot saturated solution of these electrolytes in 5 % agar solution is filled in the U-shaped tube and allowed it to cool and solidify forming a gel.
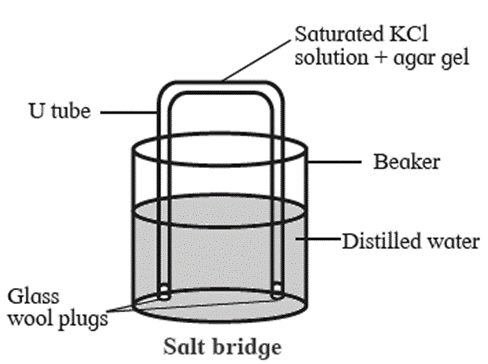
It is used to connect two half cells or electrodes forming a galvanic or voltaic cell.
Functions of salt bridge
The salt bridge serves the following functions :
- It provides an electrical contact between two solutions and thereby completes the electrical circuit.
- It prevents mixing of two solutions.
- It maintains electrical neutrality in both the solutions by transfer of ions.
- It eliminates the liquid junction potential
Formulation or short notation of galvanic cells : A galvanic cell is represented by a formula or short notation that includes electrodes, aqueous solutions of ions and other species which may or may not be involved in the cell reaction.
The following conventions are used to write the cell notation :
- The metal electrodes or the inert electrodes like platinum are placed at the ends of the cell formula.
- The galvanic cell consists of two half cells or electrodes. The electrode on the extreme left hand side is anode where oxidation takes place and it carries negative (-) charge while extreme right hand electrode is cathode where reduction takes place and it carries positive (+) charge.
- The gases or insoluble substances are placed in the interior positions adjacent to the metal electrode.
- A single vertical line (|) is written between two phases like solid electrode and aqueous solution containing ions.
- A double vertical line (||) is drawn between two solutions of two electrodes which indicates a salt bridge connecting them electrically.
- The concentration of solutions or ions or pressures of gases are written in brackets along with the substances in the cell.
- Different ions in the same solution are separated by a comma.
Examples Fe3+(aq), Fe2+(aq) |Pt; Ag+(aq) | Ag(s)
Examples of electrochemical cells :
(i) Daniel cell is represented as,
Zn(S) |Zn2+||Cu2+| Cu(s)
(1M) (1M)
(ii) Pt |H2(g)(1 atm)|H+||Ag+|Ag(s)
(1M) (1M)
Writing of cell reaction : The cell reaction corresponding to the cell notation is written on the assumption that the right hand side electrode is cathode (+) and left hand side electrode is anode (-).
The following steps are followed to write the cell reaction.
- A galvanic cell consists of two half cells or electrodes.
- Write oxidation half reaction for left hand electrode which is an anode and reduction half reaction for right hand electrode which is a cathode.
- Balance the number of electrons in the oxidation and reduction reactions.
- By adding both the reactions, overall cell reaction is obtained.
For example, consider following cell :

Oxidation half reaction at anode :
Pb(s) → Pb2+(aq) + 2e−
Reduction half reaction at cathode :
[Ag2+(aq) + e− → Ag(s)] x 2
(1M)
Overall Reaction :
Pb(s) + Ag2+(aq) → Pb2+(aq) + Ag(s)
(1M) (1M)
Q. Why is anode in a galvanic cell considered to be negative ?
According to IUPAC conventions, the electrodes of a galvanic cell where de-electronation or oxidation takes place releasing electrons is called anode.
Zn(s) → Zn2+(aq) + 2e−
The electrons released due to oxidation reaction are accumulated on the metal electrode surface charging it negatively.
Hence anode in the galvanic cell is considered to be negative.
Q. Why is cathode in a galvanic cell considered to be positive electrode ?
According to IUPAC conventions, the electrode of the galvanic cell where electronation or reduction takes place is called cathode. In this, the electrons from the metal electrode are removed by cations required for their reduction.
Cu2+(aq) + 2e− → Cu(s)
Since the electrons are lost, the metal electrode acquires a positive charge.
Hence cathode in the galvanic cell is considered to be positive.
Electrode potential and cell potential
Electrode potential : It is defined as the difference in electrical potential established by the electrode half reaction between the metal electrode surface and the solution surrounding it at constant temperature equilibrium.
Explanation : When a metal is immersed in a solution containing its ions, an oxidation (or reduction) reaction occurs, resulting in the release of electrons (or gain of electrons). As a result, an electrical double layer is formed, consisting of a charged metal surface and an ionic layer. An electrode potential is the potential that exists between the metal and the solution across this double layer.
Oxidation Potential : It is defined as the difference of electrical potential between metal electrode surface and the solution around it at equilibrium developed due to oxidation reaction at anode and at constant temperature.
Reduction Potential :It is defined as the difference of electrical potential between metal electrode surface and the solution around it at equilibrium developed due to reduction reaction at cathode and at constant temperature.
Standard potentials :
Standard state of a substance : The standard state of a substance is that state in which the substance has unit activity or concentration at 25 °C. i.e., For solution having concentration 1 molar, gas at 1 atm, pure liquids or solids arc said to be in their standard states.
Standard electrode potential : It is defined as the difference of electrical potential between metal electrode surface and the solution around it equilibrium when all the substances involved in the electrode reaction are in their standard states of unit activity or concentration at constant temperature.
Standard oxidation potential : It is defined as the difference of electrical potential between metal electrode surface and the solution around it at equilibrium due to oxidation reaction, when all the substances involved in the oxidation reaction are in their standard states of unit activity or concentration at constant temperature.
Standard reduction potential : It is defined as the difference of electrical potential between metal electrode surface and the solution around it at equilibrium due to reduction reaction, when all the substances involved in the reduction reaction are in their standard states of unit activity or concentration at constant temperature.
- According to IUPAC convention, the standard potential of an electrode due to reduction reaction at 298 K is taken as the standard reduction potential. In this active mass of the substance has unit value.
Cell potential or emf of a cell : It is defined as the potential difference between two electrodes, responsible for an external flow of electrons from the left hand electrode at higher potential (anode), to the right hand electrode at lower potential (cathode), when connected to form an electrochemical or galvanic cell.
Since there is oxidation reaction at left hand electrode (LHE) or anode and reduction reaction at right hand electrode (RHE) or cathode, emf of the galvanic Ecell is given by,
Ecell = (Eoxi)anode + (Ered)cathode
Since by IUPAC conventions, generally reduction potentials are used, hence, for the given cell,
(‘.’ Eoxi = − Ered)
∴ Ecell = (Ered)cathode − (Ered)anode
Similarly, standard emf of the cell, E0cell is given by
E0cell = (E0red)cathode − (E0red)anode
| Remember. :
• While constructing a galvanic cell from two electrodes, the electrode with higher standard potential is cathode (+) and that with lower standard potential is anode (-). • The difference in electrical potential between anode and cathode is cell voltage. |
Dependence of cell potential on concentration (Nernst equation) :
To predict the spontaneity of reactions under conditions other than standard concentration, we must first understand how the voltage of a galvanic cell varies with concentration.
The Nernst equation describes the relationship between cell voltage and concentration.
Consider following general reaction taking place in the galvanic cell.
aA + bB → cC + dD
The cell voltage is given by,
Ecell = \(E^0_{cell}-\frac{RT}{nf}ln\frac{[C]^c×[D]^d}{[A]^a×[B]^b}\)
Ecell = \(E^0_{cell}-\frac{2.303RT}{nf}log_{10}\frac{[C]^c×[D]^d}{[A]^a×[B]^b}\)
Where,
T —> temperature
R —> Gas constant
F —> Faraday
n—> Number of electrons in the redox cell reaction.
At 25 0C \(\frac{2.303RT}{F}= \frac{2.303×8.314×298}{96500} = 0.0592\)
∴ Ecell = \(E^0_{cell}-\frac{0.0592}{n}log_{10}\frac{[C]^c×[D]^d}{[A]^a×[B]^b}\)
This is Nernst equation for cell potential. It is used to calculate cell potential and electrode potentials.
Standard cell potential or standard emf of the cell :
It is defined as the difference between the standard reduction potential of cathode Eocathode (right hand electrode) and the standard potential of anode, Eoanode (left hand electrode) at the constant temperature.
E0cell = (E0oxi)anode + (E0red)cathode
OR
E0cell = E0anode − E0cathode = (E0red)RHE − (E0red)LHE
In the standard cell, the active masses of the substances taking part in the electrochemical reaction have unit value, i.e., 1 M solution or ions and 1 atm gas.
Nernst equation for the electrode potential :
The Nernst equation for the single electrode reduction potential for a given ionic concentration in the solution in the case, Mn+(aq) + ne— —> M(s) is given by
EM = \(E^0_{M}-\frac{2.303RT}{nF}log_{10}\frac{[M]}{[M^{n+}]}\)
OR
EM = \(E^0_{M}-\frac{2.303RT}{nF}log_{10}\frac{[1]}{[M^{n+}]}\)
where EM is the single electrode reduction potential.
E0M is the standard reduction electrode potential,
R is the gas constant = 8.314 JK—1 mol—1
T is the absolute temperature, _
n is the number of electrons involved in the reaction,
F is Faraday (96500 C) l
[Mn+] is the molar concentration of ions.
Calculation of cell potential and electrode potential by using Nernst equation :
(i) Calculation of cell potential :
Consider the cell
Cd(s) |Cd2+(aq)||Cu2+(aq)|Cu.
Let us first write the cell reaction
Cd(s) → Cd2+(aq)+ 2e− (oxidation at anode)
Cu2+(aq) + 2e− → Cu(s) (reduction at cathode)
Cd(s) + Cu2+(aq) → Cd2+(aq)+ Cu(s) (overall cell reaction)
Here n = 2
The potential of cell is given by Nernst equation,
Ecell = \(E^0_{cell}-\frac{RT}{nF}ln\frac{[Cd^{2+}]}{[Cu^{2+}]}\)
∴ Ecell = \(E^0_{cell}-\frac{0.0592}{2}log_{10}\frac{[Cd^{2+}]}{[Cu^{2+}]}\) at 25 0C.
(Concentration of solids and pure liquids are taken to be unity.)
(ii) Calculation of electrode potential :
Consider Zn2+(aq)|Zn(s)
The reduction reaction for the electrode is
Zn2+(aq)+ 2e− → Zn(s) Here n = 2
Applying Nernst equation, electrode potential is given by
∴ EZn = \(E^0_{Zn}-\frac{0.0592}{2}log_{10}\frac{[1]}{[Zn^{2+}]}\)
= \(E^0_{Zn}+\frac{0.0592}{2}log_{10}[Zn^{2+}]\) at 25 0C.
Where E0Zn is the standard electrode potential of zinc electrode.
Thermodynamics of galvanic cells :
Gibbs energy of cell reactions and cell potential :
Consider a galvanic cell which involves n number of electrons in the overall cell reaction. Since one mole of electrons involve the electric charge equal to one Faraday (F) which is equal to 96500 C, the total charge involved in the reaction is,
Electric charge = n x F
If Ecell is the cell potential, then Electrical work = n x F x Ecell
According to thermodynamics, electric work is equal to decrease in Gibbs energy, −ΔG, we can write,
Electric work = n x F x Ecell = −ΔG
ΔG = − nFEcell
Under standard conditions, we can write
ΔG0 = − nFE0cell
where E0cell is the standard cell potential and ΔG0 is the standard Gibbs free energy change.
E0cell is an intensive property :
Explanation :
ΔG0 is an extensive property since its value depends on the amount of substance.
If the stoichiometric equation of redox reaction is multiplied by 2 that is the amounts of substances oxidized and reduced are doubled, ΔG0 doubles. The moles of electrons transferred also doubles.
The ratio,
E0cell = \(-\frac{ΔG^0}{nF}\) becomes \(-\frac{2ΔG^0}{2nF}\) = \(-\frac{ΔG^0}{nF}\)
Therefore E0cell is independent of the amount of substance and it represents the intensive property.
Remember : For chemical reaction to be spontaneous, ΔG must be negative.
Because ΔG = −nFEcell, Ecell must be positive for a cell reaction if it is spontaneous
Standard cell potential and equilibrium constant :
For any galvanic cell, the overall cell reaction at equilibrium can be represented as,
Reactants ⇌ Products.
[For example, for Daniell cell, Zn(S) + Cu2+(aq) → Zn2+(aq) + Cu(s)]
The equilibrium constant, K for the reversible reaction will be,
K = [Products]/[Reactants]
(For example, for Daniell cell K = [Zn++]/[Cu++] )
The equilibrium constant is related to the standard free energy change ΔG0 as follows,
ΔG0 = −RT ln K
If E0cell is the standard cell potential (or emf) of the galvanic cell, then
ΔG0 = − nFE0cell
By comparing above equations,
ΔG0 = − nFE0cell = −RT ln K
∴ nFE0cell = RT ln K
∴ E0cell = \(\frac{RT}{nf}ln\,K\) OR
E0cell = \(\frac{2.303RT}{nf}log_{10}K\)
At 25°C,
\(\frac{2.303RT}{F}= \frac{2.303×8.314×298}{96500} = 0.0592\)
∴ E0cell = \(\frac{0.0592}{n}log_{10}K\)
This is a relation between equilibrium constant and E0cell
| Expressions to calculate equilibrium constant from
(i) From concentration data : Consider following a reversible cell reaction. aA + bB ⇌ cC + dD If [A], [B], [C] and [D] represent concentrations of reactants and products then the equilibrium constant K is, K = \(\frac{[C]^c×[D]^d}{[A]^a×[B]^b}\) (ii) From Thermochemical data : If ΔG0 is the standard Gibbs free energy change at temperature T then, ΔG0 = − RT ln K = − 2.303 RTlog10K (iii) From electrochemical data : if E0cell is the standard cell potential and K is the equilibrium constant for the cell reaction at a temperature T, then, E0cell = \(\frac{0.0592}{n}log_{10}K\) |
Main Page : – Maharashtra Board Class 12th-Chemistry – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter-4- Chemical Thermodynamics – Online Notes
Next Chapter : Chapter-6-Chemical Kinetics – Online Notes
We reply to valid query.