Notes-Part-2-Class-12-Chemistry-Chapter-4-Chemical Thermodynamics-Maharashtra Board

Change in enthalpy- ΔH :

Change in enthalpy, ΔH, is also state function given by

ΔH = H₂ - H₁ …(1)

where H₁ and H₂ are the enthalpies of initial and final states, respectively.

Consider a process in which a state of a system changes from an initial state A to a final state B.

Let H₁, U₁, P₁, V₁ and H₂, U₂, P₂, V₂ be the state functions of the system in initial and final states .

Then,

H₁ = U₁ + P₁V₁ and H₂ = U₂ + P₂V₂

From eq.(1)

ΔH = (U₂ + P₂V₂) — (U₁ + P₁V₁)

= (U₂ — U₁) + (P₂V₂ — P₁V₁)

= ΔU + ΔPV

where ΔU = U₂ — U₁

At constant pressure, P₁ = P₂ = P

P₂V₂ — P₁V₁= PV₂ — PV₁

= P (V₂ — V₁)

= P x ΔV

Hence, ΔH = ΔU+ PΔV

This is a relation for enthalpy change

Relationship between ΔH and ΔU for chemical reactions :

• For any thermodynamic process or a chemical reaction at constant volume, ΔV = 0.
• Since ΔH = ΔU + PΔV, at constant volume ΔH = Δ U.
• In the reactions, involving only solids and liquids, ΔV is negligibly small, hence ΔH = ΔU.
• In a chemical reaction, in which number of moles of gaseous reactants and gaseous products are equal, then change in number of moles, Δn = n₂ − n₁= 0
• Since ΔH = ΔU + ΔnRT, as Δn = 0, ΔH = ΔU.

Relationship between ΔH and ΔU for gas phase reactions :

Consider a reaction in which n₁ moles of gaseous reactant in initial state change to n₂ moles of gaseous product in the final state.

Let H₁, U₁, P₁, V₁ and H₂, U₂, P₂, V₂ represent enthalpies, internal energies, pressures and volumes in the initial and final states respectively then,

n₁A(g) → n₂B(g)

The heat of reaction is given by enthalpy change ΔH as,

ΔH = H₂ — H₁

By definition, H = U + PV

∴ H₁ = U₁ + P₁V₁ and H₂ = U₂ + P₂V₂

∴ ΔH = (U₂ + P₂V₂) — (U₁ + P₁V₁)

= (U₂ — U₁) + (P₂V₂ — P₁V₁)

Now, ΔU= U₂ — U₁

Since PV= nRT,

For initial state, P₁V₁= n₁RT

For final state, P₂V₂= n₂RT

∴ P₂V₂ — P₁V₁= n₂RT— n₁RT

= (n₂ — n₁) RT = ΔnRT

Where Δn = [Number of moles of gaseous products] — [Number of moles of gaseous reactants]

ΔH = ΔU + ΔnRT

If Q_P, and Q_V, are the heats involved in the reaction at constant pressure and constant volume respectively, then since Q_P = ΔH and Q_V = ΔU.

∴ Q_P = Q_V + ΔnRT

Expression for work done in a chemical reaction :

Consider n₁ moles of gaseous reactants A of volume V₁ change to n₂ moles of gaseous products B of volume V₂ at temperature T and pressure P.

In the initial state, PV₁ = n₁RT

In the final state, PV₂ = n₂RT

PV₂ — PV₁ = n₂RT— n₁RT = (n₂ — n₁)RT = ΔnRT

where Δn is the change in number of moles of gaseous products and gaseous reactants.

Due to net changes in gaseous moles, there arises change in volume against constant pressure resulting in mechanical work, — PΔV.

W = —PΔV= —P (V₂— V₁) = —ΔnRT

Meaning of each term :

• If n₁ = n₂, Δn = 0, W = 0. No work is performed.
• If n₂ > n₁, Δn > 0, there is a work of expansion by the system and W is negative.
• If n2 < n₁, Δn< O, there is a work of compression, hence work is done on the system and W is positive.

Different types of phase transitions :

The following are the types of phase changes :

Fusion : This involves the change of a matter from solid state to liquid state. In this heat is absorbed, hence it is endothermic (ΔH > 0).

H₂O(g) → H₂O(l)

Vaporisation or evaporation : This involves the change of a matter from liquid state to gaseous state.

In this heat is absorbed, hence it is endothermic (ΔH > 0).

H₂O(l) → H₂O(g)

Sublimation : This involves the change of matter from solid state directly into gaseous state. In this heat is absorbed, hence it is endothermic (ΔH > 0).

Camphor(s) → Camphor(g)

Process of sublimation :

The sublimation involves the conversion of a solid into vapour at constant temperature and pressure

For example,

H₂O(s) → H₂O(g),  Δ_subH = 51.08 kJ mol⁻¹ at 0 ⁰C

This conversion takes place in two steps, first melting of solid into liquid and second vaporization of the liquid.

H₂O(s)\(\underrightarrow{0^0C}\) H₂O(l),  Δ_fusH = 6.01 kJ mol⁻¹

H₂O(l) \(\underrightarrow{0^0C}\) H₂O(v),  Δ_vapH = 45.07 kJ mol⁻¹

---------------------------------------------------

H₂O(s) \(\underrightarrow{0^0C}\)  H₂O(g),  Δ_subH = 51.08 kJ mol⁻¹

It follows that

Δ_subH = Δ_fusH + Δ_vapH (See Fig.)

The increasing order of enthalpy of the given substance will be,

(s) < (l)  < (g) '

This is because the conversion of H₂O(s) to H₂O(l) and further to H₂O(g) involves absorption of heat.

Enthalpy of solution of an ionic compound :

An ionic compound dissolves in a polar solvent like water in two steps as follows :

Step-I : The ions are separated from the molecule involving crystal lattice enthalpy Δ_LH.

MX(s) → M⁺(g) + X⁻(g)

Δ_LH is always positive.

Step-II : The gaseous ions are hydrated with water molecules involving hydration energy, Δ_hydH.

M⁺(g) + xH₂O(l) → [M(H₂O)_x] ⁺

X(g) +yH₂O(l) → [X(H₂O)_y] ⁻

Δ_hydH is always negative.

The enthalpy change Δ_solH of solution is given by,

Δ_solH = Δ_LH + Δ_hydH

For example, consider enthalpy of solution of NaCl(s).

Δ_LH_NaCl = 790 kJ mol⁻¹ .

Δ_hydH_NaCl = −786 kJ mol⁻¹ .

Hence enthalpy change for solution of NaCl(S) is,

Δ_solH = Δ_LH_NaCl + Δ_hydH_NaCl

        = 790 + (− 786)

        = + 4 kJ mol⁻¹ .

Therefore dissolution of NaCl in water is an endothermic process.

Explanation: Consider the following general reaction,

aA + bB —> cC + dD

The heat of the reaction Δ_rH is the difference in sum of enthalpies of products and sum of enthalpies of reactants.

∴ Δ_rH = ∑ H_products  − ∑ H_reactants

= [cH_C + dH_D] − [aH_A + bH_B]

= ∑_PH − ∑_RH

where H represents enthalpy of the substance.

For endothermic reaction, Δ_rH is positive, (Δ_rH > 0)

For exothermic reaction, Δ_rH is negative. (Δ_rH < 0)

For example,

• N₂(g) + O₂(g) → 2NO₂(g),
• Δ_rH = 66.4 kJ (endothermic)
• 2KClO₃(s) → 2KCl(s) + 3O₂(g),
• Δ_rH = −78 kJ (exothermic)

Sign convention used for Δ_rH :

The change in enthalpy or heat of reaction Δ_rH is given by

Sum of enthalpies

Δ_rH =  [Sum of enthalpies of products ] − [Sum of enthalpies of reactants ]

       = ∑ H_products  − ∑ H_reactants

(i) If the sum of enthalpies of products, ∑_PH and reactants, ∑_RH are equal then Δ_rH for the reaction is zero, (Δ_rH  = 0).

i.e. ∑_PH = ∑_RH

∴ Δ_rH = ∑_PH − ∑_RH =0

(ii) If the sum of enthalpies of products ∑_PH is greater than the sum of enthalpies of reactants ∑_RH, then Δ_rH is positive, (Δ_rH > 0). Since such reactions take place with the absorption of heat from surroundings, given by, they are called endothermic reactions.

∴ ∑_PH > ∑ H_reactants

 Δ_rH > 0

 (iii) If the sum of enthalpies of products ∑_PH is less than the sum of enthalpies of reactants, ∑_RH then Δ_rH is negative, (Δ_rH < 0). Since in such reactions heat is given out to the surroundings, they are called exothermic reactions.

∴ ∑_PH < ∑ H_reactants

 Δ_rH < 0

Guidelines for writing thermochemical equations :

(i) Reaction is represented by balanced chemical equation for the number of moles of the reactants and the products. E. g. CH₄(g) + 2O₂(g) = CO₂(g) + 2H₂O(l)

Δ_rH⁰ = − 890 kJ mol⁻¹

(ii) The physical states of all the substances in the reaction must be mentioned. E.g. (s) for solid, (L) for liquid and (g) for gas.

(iii) Heat or enthalpy changes are measured at 298 K and 1 atmosphere (or 1 bar).

(iv) ΔH⁰ is written at right hand side of thermochemical equation.

(v) Proper sign must be indicated for ΔH⁰. For endothermic reaction ΔH⁰ is positive, ( + ΔH⁰) and for exothermic reaction ΔH⁰ is negative, (− ΔH⁰).

(vi) The enthalpy of the elements in their standard states is taken as zero. (H⁰_element = 0; H°_C(s) = 0, _(g) = 0

(vii) When all the substances taking part in the reaction are in their standard states, the enthalpy change is written as ΔH⁰.

(viii) The enthalpy of any compound is equal to its heat of formation.

(ix) In case of elements, the allotropic form must be mentioned. E.g. C_(graphite), S_(rhombic), Sn_(white).

(x) For the reverse reaction, ΔH⁰ value has equal magnitude but opposite sign.

Standard enthalpy of reaction from standard enthalpies of formation :

The standard enthalpies of formation, Δ_fH° of the compounds can be used to determine the standard enthalpy of reaction (Δ_rH°).

Δ_rH° of a reaction can be obtained by subtracting the sum of Δ_fH° values of all the reactants from the sum of Δ_fH° values of all the products with each Δ_fH° value multiplied by the appropriate coefficient of that substance in the balanced thermo-chemical equation.

Consider following reaction :

aA + bB ——> cC + dD

The standard enthalpy of the reaction is given by,

ΔH°= [ Sum Δ_fH° of the products] − [ Sum Δ_fH° of the reactants]

= ∑ Δ_fH°_products — ∑ Δ_fH°_reactants

= [cΔ_fH°_(C) + dΔ_fH°_(D)] — [a Δ_fH°_(A) + b Δ_fH°_(B)]

where a, b, c and d are the coefficients (moles) of the substances A, B, C and D respectively.

Bond enthalpy of diatomic molecules :

In case of diatomic molecules, since there is only one bond, the bond enthalpy is equal to heat of atomisation.

For example, heat of atomisation of HCl(g) is 431.9 kJ mol⁻¹.

HCl(g) —> H(g) + Cl(g), Δ_atmH° = 431.9 kJ mol⁻¹.

∴ Bond enthalpy of HCl,

Δ_atmH° = \(\frac{Δ_{atm}H}{\text{number of bonds broken}}\)

D_H—Cl = 431.9/1 = 431.9 kJ mol⁻¹. … (Bond enthalpy is generally denoted by D).

Bond enthalpy in polyatomic molecules :

• Each covalent bond in polyatomic molecules is associated with its own specific bond enthalpy.
• For polyatomic molecules the average bond enthalpy of a particular bond would be considered.

Consider bond enthalpy in H₂O. The thermochemical equation for dissociation of H₂O(g) is,

H₂O(g) —> 2H(g) + O(g), Δ_rH° = 927 kJ mol⁻¹

In this, two O — H bonds are broken. It can be represented in stepwise as follows :

H₂O(g) —> OH(g) + H(g) ΔH⁰_HO-H = 499 kJ

OH(g)  —> O(g) + H(g)   ΔH⁰_HO-H = 428 kJ

_____________________________________________________

H₂O(g) —> O(g) + 2H(g) Δ_rH° = 927 kJ

In above, even if two identical O — H bonds are broken, the energies required to break each bond are different.

The average bond enthalpy of O — H bond is,

Δ_rH° = 927/2 = 463.5 kJ mol⁻¹

Reaction and bond enthalpies :

• In a chemical reaction bonds are broken and formed.
• The enthalpies of reactions involving substances having covalent bonds are calculated by knowing the bond enthalpies of reactants and those in products.
• The calculations assume all the bonds of a given type are identical.
• Energy is always required to break a chemical bond while energy is always released in the formation of the bond.

The enthalpy change of a gaseous reactions (Δ_rH°) involving substances with covalent bonds can be calculated with the help of bond enthalpies of reactants and products. (In case of solids we need lattice energy or heat of sublimation while in case of liquids we need heat of evaporation.)

ΔH°_(reaction) = [Sum of bond enthalpies of bonds broken of reactants] — [Sum of bond enthalpies of bonds formed of products]

= ∑ ΔH°_{(bonds broken)} − ∑ ΔH°_{(bonds formes)}

For example for a following reaction,

H₂(g) + Cl₂(g) → 2HCl(g) OR

H—H(g) + Cl—Cl(g) → 2H—Cl(g)

ΔH°_(reaction) = [ΔH°_H-H + ΔH°_Cl-Cl] − 2[ΔH°_H-Cl]

If the energy required to break the bonds of reacting molecules is more than the energy released in the bond formation of the products, then the reaction will be endothermic and ΔH° reaction will be positive.

On the other hand if the energy released in the bond formation of the products is more than the energy required to break the bonds of reacting molecules then the reaction will be exothermic and ΔH° reaction will be negative.

Explanation :

Consider the formation of CO₂(g). .

In one step : C(g) + O₂(g) → CO₂(g) ΔH = − 394 kJ

In two steps : C(s) + 1/2 O₂(g) → CO(g) ΔH₁ = −83 kJ

CO(g)  + 1/2 O₂(g) → CO₂(g) ΔH₂ = −311 kJ

 ΔH = ΔH₁+ ΔH₂

− 394 kJ = − 83kJ + (−311)kJ

Hess’s law treats thermochemical equations mathematically i.e., they can be added, subtracted or multiplied by numerical factors like algebraic equations.

Applications of Hess’s law :

The Hess's law has been useful to calculate the enthalpy changes for the reactions with their enthalpies being not known experimentally.

It is used,

• To calculate heat of formation, combustion, neutralisation, ionization, etc.
• To calculate the heat of reactions which may not take place normally or directly.
• To calculate heats of extremely slow or fast reactions.
• To calculate enthalpies of reactants and products.

Characteristics :

• It occurs on its own and doesn’t require external agency.
• It proceeds in one direction and can’t be completely reversed by external stimulant.
• These processes may be fast or slow.
• These processes proceed until an equilibrium is reached.

The examples of the spontaneous processes are as follows :

• Expansion of a gas or flow of a gas from higher pressure to low pressure or a flow of heat from higher temperature to lower temperature.
• All natural processes are spontaneous.
• Flow of heat from hotter body to colder body.
• Acid-base neutralisation is a spontaneous reaction.
• Ice melts spontaneously above 0 °C.

Order in a system :

• When the atoms, molecules or ions constituting the system are arranged in a perfect order then the system is said to be in order. For example, in the solid state, the constituent atoms, molecules orions are tightly placed at lattice points in the crystal lattice.
• When solid melts forming a liquid or when a liquid vaporises, the constituents are separated and are in random motion imparting maximum disorder.
• As energy of the system decreases order increases.

Disorder in a system :

Increase in entropy is a measure of disorder in the system.

Consider following process :

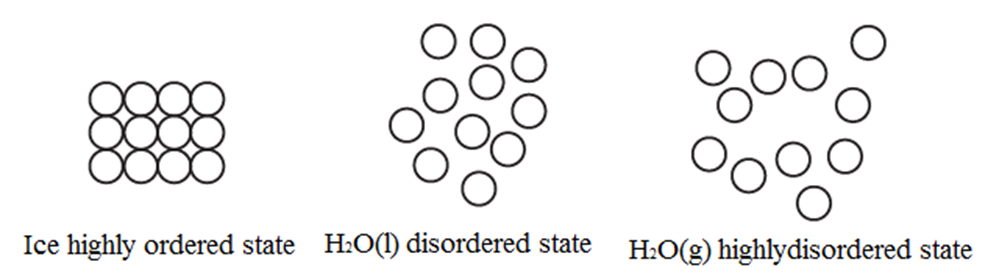
Change in order and entropy :

• The disorder or randomness is measured by entropy, denoted by S.
• Greater the disorder of a system larger is its entropy.
• Entropy of substance increases as it passes from solid to liquid to gas.
• The melting of ice and vaporisation of liquid water, in both processes entropy change ΔS > 0.

Look at the following processes :

(i) Dissolution of solid I₂ in water :

For dissolution of solid I₂,

I2(s) + aq → I₂ (aq)     …..  (ΔS > 0)

Ordered state          disordered state

In the solid I₂, there is ordered arrangement which collapses in solution increasing disorder and entropy, hence ΔS is positive.

(ii) In the dissociation of H₂(g)

H₂(g) → 2H(g) (ΔS > 0)

In the molecular state, two H atoms in every molecule are together but in atomic state the disorder is increased with the increase in entropy and hence ΔS  > 0.

Gibbs free energy and spontaneity of the process :

The total entropy change for a system and its surroundings accompanying a process is given by,

ΔS_total = ΔS_system  + ΔS_surr  

By second law, for a spontaneous process, ΔS_total > O. lf + ΔH is the enthalpy change (or enthalpy increase) for the process, or a reaction at constant temperature (T) and pressure, then enthalpy change (or enthalpy decrease) for the surroundings will be −ΔH.

∴ ΔS_surr = −ΔH/T

∴ ΔS_total = ΔS_system  + ΔS_surr  

∴ ΔS_total = ΔS_system  + (−ΔH/T)

∴ TΔS_total = TΔS_system  − ΔH

∴ TΔS_total = TΔS_system  − ΔH

∴ − TΔS_total = ΔH − TΔS_system

By Gibbs equation,

ΔG = ΔH — T ΔS

By comparing above two equations,

 ΔG = — TΔS_total

As ΔS_total increases, ΔG decreases.

For a spontaneous process, ΔS_total > 0

which is according to second law of themiodynamics.

 ∴ ΔG < 0.

Hence in a spontaneous process, Gibbs free energy decreases (ΔG < O) while entropy increases (ΔS > 0).

Therefore for a non-spontaneous process Gibbs free energy increases (ΔG > 0).

It can be concluded that for a process at equilibrium, ΔG = 0.

∴ The second law explains the conditions of spontaneity as below :

• ΔS_total > o and ΔG < 0, the process is spontaneous.
• ΔS_total < 0 and ΔG > 0, the process is non spontaneous.
• ΔS_total = 0 and ΔG = 0, the process is at equilibrium.

Temperature condition for equilibrium :

For a system at equilibrium, free energy change ΔG is,

ΔG = ΔH — T ΔS

where ΔH is enthalpy change, ΔS is entropy change at temperature, T. Since ΔG = 0 at equilibrium,

0 = ΔH — T ΔS

 TΔS = ΔH OR T = ΔH/ΔS

Hence at temperature T, changeover between forward spontaneous step and backward nonspontaneous step occurs and the system attains an equilibrium.

Here ΔH and ΔS are assumed to be independent of temperature.

Relationship between Gibb’s standard free energy change of the reaction and equilibrium constant K:

Consider following reversible reaction,

aA + bB ⇌ cC + dD

The reaction quotient Q is,

Q = \(\frac{[C]^c×[D]^d}{[A]^a×[B]^b}\)

The free energy change ΔG for the reaction is

ΔG = ΔG° + RT ln Q

Where ΔG° is the standard free energy change.

At equilibrium

Q = \(\frac{[C]^e_c×[D]^e_d}{[A]^e_a×[B]^e_b}\) =K

ΔG = ΔG° + RT ln K

 at equilibrium ΔG = 0

 0 = ΔG° + RT ln K

 ΔG° = − RT ln K

 ΔG° = − 2.303 RT log₁₀K.