Structure of Atoms and Nuclei
Maharashtra Board-Class-12th-Physics-Chapter-15
Notes-Part-1
|
Topics to be Learn : Part-1
|
Introduction :
- Greek philosophers Leucippus (-370 BC) and Democritus (460 – 370 BC) propose, that matter is made of indivisible parts called atoms.
- According to Dalton (1766-1844) to his atomic theory (i) matter is made up of indestructible particles, (ii) atoms of a given element are identical and (iii) atoms can combine with other atoms to form new substances.
- In 1887, J. J. Thomson discovered electrons and developed his atomic model.
- In 1911, Ernest Rutherford proposed the nuclear atom model.
- In 1913, Niels Bohr proposed the quantum theory of the electronic structure of the atom.
- In 1924, Wolfgang Pauli discovered the exclusion principle.
- In 1932, Sir James Chadwick discovered the neutron.Bohr proposed the liquid drop model of nucleus in 1936.
- In 1942, Enrico Fermi constructed the first atomic reactor (nuclear reactor) and achieved the first controlled self-sustaining nuclear reaction.
- The first atomic bombs, based on nuclear fission, were detonated in 1945.
- In 1952, Edward Teller and others studied the idea of a fusion bomb (the hydrogen bomb), and the H-bomb was detonated.
- In 1951, the first nuclear reactor [Experimental Breeder Reactor 1 (EBR 1)] was developed. It produced electrical energy. Walter Zinn (1906-2000) was the lead scientist on this project.
- Various types of nuclear reactors are currently in use for generating electrical energy, producing radioisotopes, and conducting research.
Thomson’s Atomic Model:
- Sir J. J. Thomson (1856-1940), a British physicist, proposed the first model of an atom with a substructure in 1898.
- An atom, according to this model, is a sphere with a uniform distribution of positive charge and electrons embedded in it, resulting in an electrically neutral and stable atom.
Drawbacks : This model, known as the plum-pudding model, failed to account for the observed scattering of α-particles and spectra of various elements. It can be shown that the Thomson atom cannot be stable.
Geiger-Marsden Experiment:
α -particle scattering experiment :
- Following his pioneering work on radioactivity and the characteristics of α-particles, Sir Ernest Rutherford (1871 — 1937), a New Zealand British scientist, observed that a narrow stream of α-particles gets somewhat broadened or scattered on passing through a thin metal foil or mica sheet.
- Since most of the α -particles remained undeviated, this suggested that atoms could not be solid spheres as proposed in Thomson's model and kinetic theory of gases.
- To probe into the effects of the distribution of an atom’s mass and charge on the α-particles, he suggested his collaborator Geiger and the latter’s student Marsden to see if any α -particles are scattered through a large angle.
The Geiger-Marsden α-scattering (or gold foil) experiment (1908) : Geiger and Marsden made a stream of α-particles strike a very thin gold foil about 40 pm thick. Their apparatus is shown schematically in Fig.
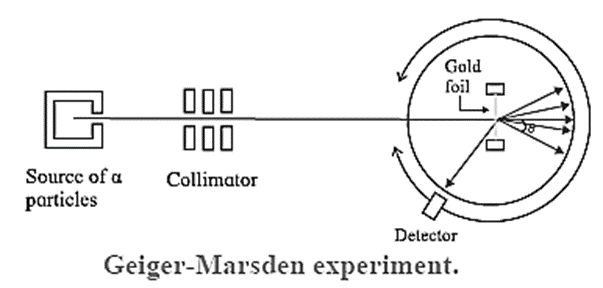
Apparatus : A radium compound, an intense source of α -particles, was placed in the lead enclosure, provided with a small hole. The stream of α-particles was collimated by lead bricks. The number of particles scattered through each angle θ were counted by a rotatable detector. The detector consisted of a small zinc sulphide screen at the focus of a low power microscope. Each incidence produced a scintillation—a momentary pinpoint of fluorescence. These scintillations were observed and counted using the microscope.
Observations : Most of the alpha particles passed straight through the foil while a few were deflected (scattered) through various scattering angles.
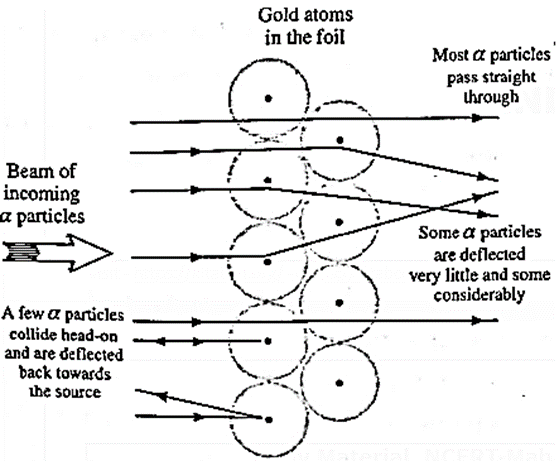
A typical scattering angle is shown by θ in the figure. Only about 0.14% of the incident alpha particles were scattered through angles larger than 0.1o. Even out of these, most were deflected through very small angles. About one alpha particle in 8000 was deflected through angle larger than 90o and a fewer still were deflected through angles as large as 180o.
Rutherford’s Atomic Model:
Rutherford’s model of the nuclear atom (1911) :
- An atom has a very small nucleus which contains ‘all the positive charge and almost all the mass of the atom.
- The nuclear size (radius about 10−44 m) is very small compared to the atomic size (radius about 10−10 m), about 10000 times smaller.
- Electrons revolve in circular orbits around the nucleus. The electrostatic force (Coulomb force) of attraction between the positively charged nucleus and the negatively charged electron is the centripetal force required for the orbital motion of the electron.
- Since an atom as a whole is electrically neutral, the positive charge on the nucleus must be equal to the total negative charge of all the orbiting electrons.
- As this model resembles the solar system, it is known as the planetary atom model.
Difficulties with Rutherford’s Model:
- Rutherford proposed that electrons revolve in circular orbits around the atomic nucleus. The circular motion is an accelerated motion. An accelerating charge constantly emits energy, according to classical electromagnetic theory. Therefore, an electron during its orbital motion, should go on radiating energy. Due to the loss of energy, the radius of its orbit should go on decreasing. Therefore, the electron should move along a spiral Path and finally fall into the nucleus in a very short time, of the order of 10-16 s in the case of a hydrogen atom. Thus, the atom should be unstable. We exist because atoms are stable.
- As the electron proceeds along its spiral path, the radius of its orbit gradually decreases. As a result, the electron's speed and frequency of revolution would continue to increase. As a result, the electron would emit radiation with a constantly shifting frequency, giving rise to a continuous spectrum. The atomic spectrum, on the other hand, is a line spectrum.
Atomic Spectra:
Emission spectrum of a substance :
- The distribution of electromagnetic radiations emitted by a substance when heated or attacked by electrons, ions, or photons is referred to as its emission spectrum.
- Unless the temperature of the substance is very high and the distribution is continuous, the distribution is sorted in order of rising (or decreasing) frequency (or wavelength).
- The spectrum could be either a line spectrum or a band spectrum. The intensities associated with certain frequencies differ.
- The absorption spectrum is formed by absorption of electromagnetic radiation when the substance is exposed to radiation of all frequencies.
Wavelengths of lines in the hydrogen spectrum :
- Hydrogen atom also emits radiation at some other values of wavelengths in the ultraviolet (UV), the infrared (IR) and at longer wavelengths.

- The spectral lines can be divided into groups known as series with names of the scientists who studied them.
- The series, starting from shorter wavelengths and going to larger wavelengths are called Lyman series, Balmer series, Paschen series, Brackett series, Pfund series, etc.
- In each series, the separation between successive lines decreases as we go towards shorter wavelength and they reach a limiting value.
- Fig. shows the first three series. The limiting value of the wavelength for each series is shown by dotted lines.
Formula: 1/λ = \(R[\frac{1}{n^2}-\frac{1}{m^2}]\) where λ is the wavelength of a line in the hydrogen spectrum, R is a constant, now called the Rydberg constant, and n and m are integers with n = 1,2,3,...and m = n+ 1, n+2, n+3,
For a fixed value of n, λ decreases as m increases and has minimum value as m → ∞. λ = n2/R as m → ∞.
Bohr’s Atomic Model:
He made three postulates which defined his atomic model. These are given below.
- (i) The electron revolves with a constant speed in a circular orbit around the nucleus. The centripetal forcenecessary for the circular motion is providedby the electrostatic force of attraction betweenthe electron and the nucleus.
- (ii) The electron can revolve without radiating energy only in certain orbits, called allowed or stable orbits, in which the angular momentum of the electron is equal to an integral multiple of h/2π where h is Planck's constant.
- (iii) An electron can make a transition from one of its orbit to another orbit having lower energy. In doing so, it emits a photon of energy equal to the difference in its energies in the two orbits.
Radii of the Orbits:
Consider an electron revolving in the nth orbit around the nucleus of an atom with the atomic number Z. Let m and —e be the mass and charge of the electron, r the radius of the orbit and v the linear speed of the electron.
According to Bohr’s first postulate, centripetal force on the electron = electrostatic force of attraction exerted on the electron by the nucleus.
∴ \(\frac{mv^2}{r}=\frac{Ze^2}{4πε_0r^2}\) ...(1)
where ε0 is the permittivity of free space.
∴ v2 = \(\frac{Ze^2}{4πε_0mr}\) ……(2)
According to Bohr’s second postulate, the orbital angular momentum of the electron,
mvr = \(\frac{nh}{2π}\)
where h is Planck's constant and n is the principal quantum number which takes integral values 1, 2, 3, ..., etc.
∴ v = \(\frac{nh}{2πmr}\)
∴ v2 = \(\frac{n^2h^2}{4π^2m^2r^2}\) ….(4)
Equating the right hand sides of Eqs. (2) and (4),
\(\frac{Ze^2}{4πε_0mr}\) = \(\frac{n^2h^2}{4π^2m^2r^2}\)
∴ r = \((\frac{ε_0h^2}{πmZe^2})n^2\) ….(5)
Since, ε0, h, Z, m and e are constants, it follows that r ∝ n2, i.e., the radius of a Bohr orbit of the electron in an atom is directly proportional to the square of the principal quantum number.
Centripetal acceleration of an electron in a Bohr orbit of a hydrogen atom :
Centripetal acceleration a = v2/r =
Substituting v2 From eq. (2)
∴ a = \(\frac{Ze^2}{4πε_0mr}.\frac{1}{r}\) = \(\frac{Ze^2}{4πε_0mr^2}\)
Hence substituting for r from eq. (5)
a = \(\frac{Ze^2π^2m^2Z^2e^4}{4πε_0mε_0^2n^4h^4}\) = \((\frac{πmZ^3e^6}{4ε_0^3h^4}).\frac{1}{n^4}\)
Since all the quantities within the bracket are constants,
a ∝ 1/n4
Hence the centripetal acceleration of an electron in a Bohr orbit of a hydrogen atom is inversely proportional to the fourth power of the principal quantum number.
Q. Derive an expression for the linear speed of an electron in a Bohr orbit. Hence, show that it is inversely proportional to the principal quantum number.
Ans. Consider an electron revolving in the nth Bohr orbit around the nucleus of an atom with the atomic number Z. Let m and − e be the mass and charge of the electron, r the radius of the orbit and v the linear speed of the electron.
According to Bohr's first postulate, centripetal force on the electron = electrostatic force of attraction exerted on the electron by the nucleus.
∴ \(\frac{mv^2}{r}=\frac{Ze^2}{4πε_0r^2}\) …..(1)
where ε0 is the permittivity of free space.
∴ mv2 = \(\frac{Ze^2}{4πε_0r}\) …..(2)
According to Bohr's second postulate, the orbital angular momentum of the electron is quantized :
mvr = \(\frac{nh}{2π}\) ….(3)
where h is Planck's constant and n is the principal quantum number which takes integral values 1, 2, 3, ..., etc.
∴ r = \(\frac{nh}{2πmv}\)
Substituting this expression for r in Eq. (2), we get,
mv2 = \(\frac{Ze^2}{4πε_0}.\frac{2πmv}{nh}\) ….(4)
∴ v = \(\frac{Ze^2}{2ε_0nh}\) ….(5)
∴ v ∝ 1/n … (as Z, e, ε0 and h are constants)
[Note : In this topic, unless stated otherwise, m ≡ me, r ≡ rn and v ≡ vn]
Stationary orbit : In the Bohr model of the hydrogen atom, a stationary orbit refers to any of the discrete allowed orbits such that the electron does not radiate energy while it is in such orbits.
Energy of the Electrons:
Expression for the energy of an electron in the atom :
Consider the electron revolving in the nth orbit around the nucleus of an atom with the atomic number Z.
Let m and -e be the mass and the charge of the electron, r the radius of the orbit and v the linear speed of the electron.
According to Bohr’s first postulate, centripetal force on the electron = electrostatic force of attraction exerted on the electron by the nucleus
∴ \(\frac{mv^2}{r}=\frac{Ze^2}{4πε_0r^2}\) …..(1)
where ε0 is the permittivity of free space.
∴ Kinetic energy (KE) of the electron = \(\frac{1}{2}mv^2=\frac{Ze^2}{8πε_0r}\) …..(2)
The electric potential due to the nucleus of charge +Ze at a point at a distance r from it is
V = \(\frac{1}{4πε_0}.\frac{Ze}{r}\)
∴ Potential energy (PE) of the electron = charge on the electron x electric potential
= \(-e×\frac{1}{4πε_0}.\frac{Ze}{r}\) = \(-\frac{Ze^2}{4πε_0r}\) ……(3)
Hence, the total energy of the electron in the nth orbit is
E = KE + PE = \(-\frac{Ze^2}{4πε_0r}\) + \(\frac{Ze^2}{8πε_0r}\)
∴ E = \(-\frac{Ze^2}{8πε_0r}\) …..(4)
This shows that the total energy of the electron in the nth orbit of the atom is inversely proportional to the radius of the orbit as Z, ε0 and e are constants.
The radius of the nth orbit of the electron is
r = \(\frac{ε_0h^2n^2}{πmZe^2}\) ….(5)
where h is Planck's constant.
From Eqs. (4) and (5), we get,
En = \(-\frac{Ze^2}{8πε_0}(\frac{πmZe^2}{ε_0h^2n^2})\) = \(-\frac{mZ^2e^4}{8ε_0^2h^2n^2}\) ….(6)
This gives the expression for the energy of the electron in the nth Bohr orbit. The minus sign in the expression shows that the electron is bound to the nucleus by the electrostatic force of attraction.
As m, Z, e, ε0 and h are constant, we get
En ∝ 1/n2
i.e., the energy of the electron in a stationary energy state is discrete and is inversely proportional to the square of the principal quantum number.
Substituting the values of the constants m, e, h_and ε0 in the above equation, we get
En = \(−13.6\frac{Z^2}{n^2}\) (in eV)
- The first orbit ( n = 1) which has minimum energy, is called the ground state of the atom.
- Orbits with higher values of n and therefore, higher values of energy are called the excited states of the atom.
- If the electron is in the nth orbit, it is said to be in the nth energy state.
For hydrogen Z = 1
En = \(-\frac{13.6}{n^2}\)(in eV)
Binding energy : Binding energy of an electron in an atom is defined as the minimum energy that should be provided to an orbital electron to remove it from the atom such that its total energy is zero.
If we provide the energy \(\frac{mZ^2e^4}{8ε_0^2h^2n^2}\) [ref. eq no (6) from above] to the electron, its total energy will become zero, i.e., it will become just free from the influence of the host atom.
Therefore, the binding energy of the electron,
BE = −En = \(\frac{mZ^2e^4}{8ε_0^2h^2n^2}\) ….(7)
Excitation energy of an electron in an atom : The energy required to transfer an electron from the ground state to an excited state (a state of higher energy) is called the excitation energy of the electron in that state.
Ionization energy : Ionization energy of an electron in an atom is defined as the minimum energy required to remove the least strongly bound electron from a neutral atom such that its total energy is zero.
Remeber : Since a hydrogen atom has only one electron, the ionization energy is also the binding energy of the electron in the first orbit.
Ground state of an atom : Ground state of an atom is defined as the lowest stable energy state of the atom.
Different series of spectral lines for hydrogen :
According to Bohr’s model of the hydrogen atom,an atom exists most of the time in one of a number of stable and discrete energy states. The various states arranged in order of increasing energy constitute the energy level diagram of the atom, as shown in below Fig. for the hydrogen atom. Here, the higher (less negative) energies are at the top while the lower (more negative) energies are toward the bottom.
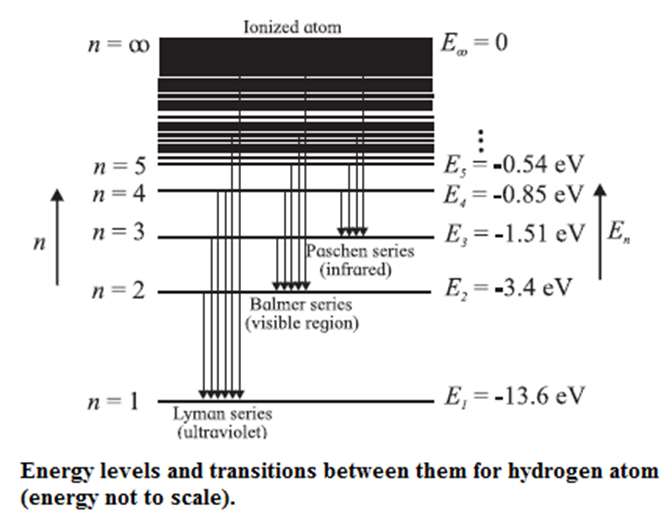
According to Bohr’s theory, electromagnetic radiation of a particular wavelength is emitted when there is a transition of the electron from a higher energy state to a lower energy state. Let the quantum number n = m represent a higher energy state and n = n represent a lower energy state (m > n).
The formation of the different series of spectral lines is explained from the energy level diagram.
Lyman series : This series in the far UV region of the spectrum arises due to the transitions of the electron to n = 1 from m = 2, 3, 4, ..., etc. The wavelengths (λ) of the spectral lines in this series are given by
1/λ = \(R(\frac{1}{1^2}-\frac{1}{m^2})\) ….(m=2,3,4,..., ∞)
where R is the Rydberg constant.
Balmer series : This series in the visible region of the spectrum arises due to the transitions to n = 2 from m = 3, 4, 5, ..., etc. The wavelengths (λ) of the spectral lines in this series are given by
1/λ = \(R(\frac{1}{2^2}-\frac{1}{m^2})\) ….(m=3,4,5, ..., ∞)
Paschen, Brackett and Pfund series : These three series in the infrared region of the spectrum arise due to the transitions to n = 3, 4 and 5, respectively from m = n + 1, n + 2, etc. The wavelengths (λ) of the lines are given by
(Paschen) 1/λ = \(R(\frac{1}{3^2}-\frac{1}{m^2})\) …(m=4, 5, 6, ..., ∞)
(Brackett) 1/λ = \(R(\frac{1}{4^2}-\frac{1}{m^2})\) …(m=5, 6, 7, ..., ∞)
(Pfund) 1/λ = \(R(\frac{1}{5^2}-\frac{1}{m^2})\) …(m=6, 7, 8, ..., ∞)
In each series, the smallest quantum of radiation (smallest frequency, longest wavelength) arises from the transition from m =n + 1 to n, and the largest quantum (highest frequency, shortest wavelength— short wavelength limit or series limit) is for the transition from m = ∞ to n.
Bohr's formula for a hydrogen spectral line (expression for the wave number) :
According to Bohr’s third postulate for the model of the hydrogen atom, an atom radiates energy only when an electron jumps from a higher energy state to a lower energy state and the energy of the quantum of electromagnetic radiation emitted in this process is equal to the energy difference between the two states of the electron. This emission of radiation gives rise to a spectral line.
The energy of the electron in a hydrogen atom, when it is in an orbit with the principal quantum number n, is
En = \(-\frac{me^4}{8ε_0^2h^2n^2}\)
where m =mass of electron, e = electronic charge, h = Planck's constant and ε0 = permittivity of free space.
Let Em be the energy of the electron in a hydrogen atom when it is in an orbit with the principal quantum number m and En, its energy in an orbit with the principal quantum number n, n < m. Then
Em = \(-\frac{me^4}{8ε_0^2h^2m^2}\) and En = \(-\frac{me^4}{8ε_0^2h^2n^2}\)
Therefore, the energy radiated when the electron jumps from the higher energy state to the lower energy state is
Em − En = \(-\frac{me^4}{8ε_0^2h^2m^2}-(-\frac{me^4}{8ε_0^2h^2n^2})\)
= \(\frac{me^4}{8ε_0^2h^2}(\frac{1}{n^2}-\frac{1}{m^2})\)
This energy is emitted in the form of a quantum of radiation (photon) with energy hv, where v is the frequency of the radiation.
∴ Em − En = hv
∴ v = \(\frac{E_m-E_n}{h}\) = \(\frac{me^4}{8ε_0^2h^3}(\frac{1}{n^2}-\frac{1}{m^2})\)
The wavelength of the radiation is λ = c/v, where c is the speed of radiation in free space.
The wave number, \(\bar{v}\) = 1/λ = v/c
∴ \(\bar{v}\) = 1/λ = \(\frac{me^4}{8ε_0^2h^3c}(\frac{1}{n^2}-\frac{1}{m^2})\)= \(R(\frac{1}{n^2}-\frac{1}{m^2})\)
where R = \(\frac{me^4}{8ε_0^2h^3c}\) is a constant called the Rydberg constant.
This expression gives the wave number of the radiation emitted and hence that of a line in hydrogen spectrum.
[Note : Z =1 for hydrogen atom]
For the Laymen series : n= 1, m =2,3,4,..., ∞
1/λL = \(R(\frac{1}{1^2}-\frac{1}{m^2})\)
and for the shortest wavelength line in this series,
1/λLs = \(R(\frac{1}{1^2})\) as m = ∞
For the Balmer series : n= 2, m = 3,4,5, ..., ∞
1/λB = \(R(\frac{1}{2^2}-\frac{1}{m^2})\)
and for the shortest wavelength line in this series,
1/λBs = \(R(\frac{1}{4})\) as m = ∞
Q. Show that the energy of the electron in the nth stationary orbit in the hydrogen atom is En = —Rch/n2.
Ans. The energy of the electron in the nth stationary orbit in the hydrogen atom is
En = \(-\frac{me^4}{8ε_0^2h^2n^2}\)
and the Rydberg constant is
R = \(\frac{me^4}{8ε_0^2h^3c}\)
where m = mass of electron, e =electr0nic charge, h = Planck's constant, c = speed of light in free space and ε0 = permittivity of free space.
∴ En/R = \(-\frac{me^4}{8ε_0^2h^2n^2}×\frac{8ε_0^2h^3c}{me^4}\) = \(-\frac{ch}{n^2}\)
∴ En = \(-\frac{Rch}{n^2}\)
Limitations of Bohr’s Model:
- It could not explain the line spectra of atoms other than hydrogen. Even for hydrogen, more accurate study of the observed spectra showed multiple components in some lines which could not be explained on the basis of this model.
- The intensities of the emission lines seemed to differ from line to line and Bohr’s model had no explanation for that.
- On the theoretical side, the model was similarly unsatisfactory because it arbitrarily assumed orbits obeying a specific criteria to be stable. That assumption has no theoretical support. The model cannot account for the Zeeman effect and Stark effect
De Broglie provided some explanation for the third shortcoming (i.e., the theoretical basis for the second postulate in Bohr's atomic model).
De Broglie’s Explanation:
By the de Broglie equation, the wavelength associated with an electron having momentum p = mv is
λ = h/p = h/mv …...(1)
In a hydrogen atom in its ground state, the de Broglie wavelength associated with the electron is the same as the circumference of the first Bohr orbit.
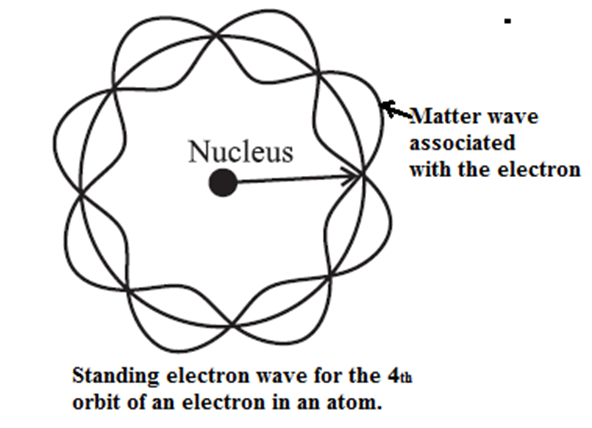
Therefore, the electron orbit in a hydrogen atom in its ground state corresponds to one complete electron wave joined on itself.
Thus, a stationary orbit can be interpreted as one which can accommodate an integral number of de Broglie wavelength so that the associated matter wave will be in phase with itself and constructive interference will allow a standing wave along the orbit.
Therefore, for a stationary Bohr orbit of circumference 2πr,
2πr = nλ
where n is a positive integer.
∴ 2πr = \(\frac{nh}{mv}\) …….[From Eq. (1)]
∴ Angular momentum, L = mvr = \(n(\frac{h}{2π})\)
which is just the Bohr condition of angular momentum quantization for stable or allowed orbits.
Class-12-Physics-Chapter-15-Structure of Atoms and Nuclei-Text Book Class-12-Physics-Chapter-15-Structure of Atoms and Nuclei-Notes Class-12-Physics-Chapter-15-Structure of Atoms and Nuclei-Solution Class-12-Physics-All 16 Chapters Notes (16-PDF) Class -12 -Physics -All 16 Chapters Solutions (16-PDF) Class 12-Physics-All Notes and Solutions-Class-12-Physics-16 Chapters-Maharashtra Board
Main Page : – Maharashtra Board Class 12th-Physics – All chapters notes, solutions, videos, test, pdf. Previous Chapter : Chapter-14-Dual Nature of Radiation and Matter –Online Notes Next Chapter : Chapter-16-Semiconductor Devices – Online Notes
We reply to valid query.