Notes-Part-1
|
Topics to be Learn : Part-1
|
Introduction :
Chemical kinetics :
Chemical kinetics is a subfield of physical chemistry that studies the mechanisms and rates of chemical reactions as well as how different variables like temperature, pressure, catalyst, etc. affect these rates.
Importance of chemical kinetics :
- It deals with the study of the rates and mechanism of reactions.
- The effect of temperature on the reaction rates can be studied.
- The influence of catalysts can be studied.
- The conditions for altering the rates and mechanisms of chemical reactions can be predicted.
- Thermodynamic parameters like energy, enthalpy changes, ΔS, ΔG of the reactions can be calculated.
Classification of reactions based on rates of the reactions :
According to the rates of the reactions, they can be classified as :
(i) Fast reactions : In this, reactants react almost instantaneously, e.g., neutralisation reaction between H+ and OH−, forming water.
H+(aq) + OH−(aq) → H2O(l).
(ii) Very slow reactions : In this, the reactants react extremely slow, so that there is no appreciable change in the concentrations of the reactants over a long period of time. E.g., reaction of silica with mineral acids, rusting of iron, etc.
(iii) Moderately slow reactions : In this, the reactants react moderately slow with a measurable velocity, e.g., the hydrolysis of the esters.
CH3COOC2H5 + H2O \(\underrightarrow{H^+}\) CH3COOH + C2H5OH
Factors affecting the rate of a chemical reaction :
- Nature of the reactants.
- The concentration of the reactants. In case of a gaseous reaction the rate depends on the pressures of the reactants.
- Temperature of the reaction.
- The presence of a catalyst and its nature.
Rate of reactions :
Rate of reactions : The rate of reaction describes how rapidly the reactants are consumed or the products are formed.
Rate of a reaction = \(\frac{\text{Change in concentration of the reactants or products}}{\text{Time required for the change}}\)
It is often expressed in mol dm−3s−1
Rate of the reaction in terms of the concentration of the reactants :
If c1 and c2 are the concentrations of the reactant A at time t1 and t2 respectively, then, the change in concentration, Δc = c2 − c1
Since c2 < c1the term Δc is negative often written as — Δc.
The time interval is, Δt = t2 − t1
If Δ [A] is the change in concentration of A, then
Δ [A] = c2 − c1
∴ Rate of consumption of A = \(\frac{-[ΔA]}{Δt}\)
∴ Rate of the reaction = \(\frac{-Δc}{Δt}\)
Rate of the reaction in terms of the concentration of the products :
If x1 and x2 are the concentrations of the product B at time t1 and t2 respectively, then the change in concentration, Δx = x2 − x1
‘.’ x2 > x1, the term Δx is positive.
The time interval is, Δt = t2 − t1
If ΔB is the change in concentration of product B, then
Δ [B] = x2 − x1 = Δx
∴ Rate of formation of B = \(+\frac{Δ[B]}{Δt}\)
∴ Rate of the reaction = \(\frac{Δx}{Δt}\)
Average rate of chemical reaction : It is expressed as a finite change in concentration (−Δc) of the reactant divided by the time interval (Δt) for the change in concentration.
∴ Average rate R = \(\frac{-Δc}{Δt}\)
Explanation :
Consider a reaction, A → B
The rate of a reaction,
R = \(\frac{-Δ[A]}{Δt}\)=\(\frac{-Δc}{Δt}\)=\(\frac{c_2 - C_1}{t_2-t_1}\)
∴ Average rate = \(\frac{-Δc}{Δt}\) (in mol dm−3s−1)
Δc is negative, since the concentration of the reactant decreases with the time.
The rate of a reaction is also measured in terms of a finite change in the concentration (Δx) of the product divided by the time interval (Δt), for the change.
For the reaction, Δ[B] = Δx
Rate = \(\frac{Δ[B]}{Δt}\)=\(\frac{x_2 - x_1}{t_2-t_1}\)
∴ Average rate = \(\frac{Δx}{Δt}\) (in mol dm−3s−1)
Instantaneous rate of a reaction : It is defined as a rate of a reaction at a specific instant during a course of the reaction.
If the average reaction rate is calculated over shorter and shorter intervals (making Δt very small) then instantaneous rate is obtained.
In case of reactant A, the instantaneous rate is represented as, R =
and in case of product B, it is represented as R =
Determining Instantaneous rate of a reaction :
(1) The instantaneous rate is expressed as an infinitesimal change in concentration (−dc) of the reactant with the infinitesimal change in time (dt).
For a reaction, A → B let an infinitesimal change in A be −dc in time dt, then
Rate = \(\frac{d[A]}{dt}\)
Hence, it is represented as,
∴ Instantaneous rate = \(\frac{-d[A]}{dt}\)
Negative sign indicates decrease in the concentration of A.
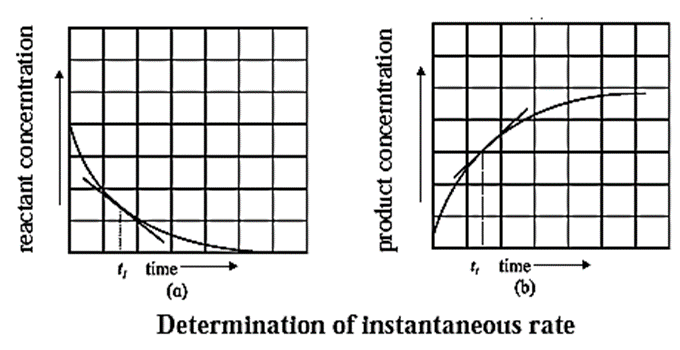
It is obtained by drawing a tangent to the curve obtained by plotting the concentration against the time. Hence, the slope at a given point represents the instantaneous rate of the reaction.
(2) The instantaneous rate can also be expressed as an infinitesimal change (or increase) in the concentration of the product with the infinitesimal change in time (dt).
Let dB be an infinitesimal change in the concentration of product B in time dt, then
Rate = \(\frac{d[B]}{dt}\) = \(\frac{dx}{dt}\)
Hence,
Instantaneous rate = \(\frac{dx}{dt}\)
It is obtained from the slope of the curve obtained by plotting the concentration of the product against time.
The instantaneous rate is more useful in obtaining the rate law integrated equations.
Rate of a reaction in terms of change in concentration of each constituent in the reaction : aA + bB → cC + dD :
The rate of a reaction may be expressed in terms of decrease in concentration of the reactants or increase in concentration of the product per unit time,
For the given reaction,
aA + bB → cC + dD
Rate of a reaction = \(-\frac{1}{a}\frac{Δ[A]}{Δt}\) = \(-\frac{1}{b}\frac{Δ[B]}{Δt}\)
= \(+\frac{1}{c}\frac{Δ[c]}{Δt}\) = \(+\frac{1}{d}\frac{Δ[D]}{Δt}\)
Or
Rate of a reaction = \(-\frac{1}{a}\frac{d[A]}{dt}\) = \(-\frac{1}{b}\frac{d[B]}{dt}\)
= \(+\frac{1}{c}\frac{d[c]}{dt}\) = \(+\frac{1}{d}\frac{d[D]}{dt}\)
| Expression for rates of reaction for : 2N2O(g) → 4NO2(g) + O2(g)
For the given reaction, Rate of a reaction R = \(-\frac{1}{2}\frac{d[N_2O_5]}{dt}\) = \(+\frac{1}{4}\frac{d[NO_2]}{dt}\) = \(+\frac{d[O_2]}{dt}\) |
Rate of reaction and reactant concentration :
The rate of a reaction at a given temperature for a given time instant depends on the concentration of reactant. Such rate-concentration relation is the rate law.
Rate law (or differential rate law) :It is defined as an experimentally determined mathematical equation which expresses the rate of a chemical reaction in terms of molar concentrations of the reactants which influence the rate of the reaction.
For example, for a reaction, A + B → Products
By rate law, Rate = R = k [A] x [B]
where k is a rate constant and [A] and [B] are molar concentrations of the reactants A and B respectively.
Relationship between coefficients of reactants in a balanced equation for an overall reaction and exponents in rate law :
Consider the following reaction,
aA + bB → products
If the rate of the reaction depends on the concentrations of the reactants A and B, then, by rate law,
R ∝ [A]a [B]b
∴ R = k [A]a [B]b
where [A] = concentration of A and [B] = concentration of B
The proportionality constant k is called the velocity constant, rate constant or specific rate of the reaction.
a and b are the exponents or the powers of the concentrations of the reactants A and B respectively when observed experimentally.
The exponents or powers may not be necessarily a and b but may be different x and y depending on experimental observations. Then the rate R will be,
R = k [A]x × [B]y
For example, if x = 1 and y = 2, then,
R = k [A] × [B]2
Examples of rate law with illustrations:
Consider following examples :
(i) H2(g) + I2(g) → 2HI(g)
R = k [H2] [I2]
(ii) 2H2O2(g) → 2H2O(l) + O2(g)
Experimentally it is observed that the rate of the reaction is proportional to the concentration of H2O
∴ R = k [H2O2]
(iii) NO2(g) + CO(g) → NO(g) + CO2(g)
Experimentally it is observed that rate of the reaction does not depend on the concentration of CO but it is proportional to [NO2]2.
∴ R = k [NO2]2
Applications of the rate law :
- Knowing the rate law and the rate constant allows you to calculate the rate of any reaction at a given concentration.
- The rate law and rate constant can be used to estimate the concentration of reactants or products at any point during the course of a reaction.
- Simple or complex chemical reactions' mechanisms can be predicted and studied.
Rate constant : The rate constant of a chemical reaction is defined as the rate of the chemical reaction when the concentration (or active masses) of each reactant has unit value, i.e., 1 mol dm−3 in the case of solution and the pressure is 1 atm in case of gases, e.g., for a reaction, A → products, Rate R = k[A].
If [A] = 1 mol dm−3, then k = R.
The rate constant of a reaction depends on the following factors :
- Nature of the reactants.
- Temperature of the reaction. As the temperature increases, the velocity constant (rate constant) increases.
- The conditions of the reactions like the presence of the catalyst, solvent, pH, etc.
- It does not depend on the concentration of the reactants. But if one or more substances are in excess concentration, then the order of the reaction is independent of them.
Characteristics of rate constant :
- The rate constant depends upon the nature of the reaction.
- Higher the value of the rate constant, faster is the reaction.
- Lower the value of the rate constant, slower is the reaction.
- By increasing the temperature, the magnitude of the rate constant increases.
- For the given reaction, the rate constant has higher value in the presence of a catalyst than in the absence of the catalyst.
- The reactions having lower activation energy have higher values for rate constants.
Q. For the reaction 2A + 2B → 2C +D, if concentration of A is doubled at constant [B] the rate increases by a factor of 4. If the concentration of B is doubled with [A] being constant the rate is doubled. Write the rate law of the reaction.
Rate = R1 = k [A]x [B]y When concentration of A = [2A] and [B] = constant, R2 = 4R1 = k [2A]x [B]y When [A] = constant and concentration of B = [2B], R3 = 2R1 = k [A]x [2B]y \(\frac{R_2}{R_1}=\frac{k[2A]^x[B]^y}{k[A]^x[B]^y}\) = 4 ∴ 2x = 4 ∴ x = 2 \(\frac{R_2}{R_1}=\frac{k[A]^x[2B]^y}{k[A]^x[B]^y}\) = 2 2y = 2 y = 1 Hence order with respect to A is 2 and with respect to B is 1. By rate law, Rate = k [A]2 [B].
Order of the reaction :
Order of a chemical reaction : The order of a chemical reaction is defined as the number of molecules (or atoms) whose concentrations influence the rate of the chemical reaction. OR The order of a chemical reaction is defined as the sum of the powers (or exponents) to which the concentration terms of the reactants are raised in the rate law expression for the given reaction.
Explanation : Consider a reaction, n1A + n2B → Products where n1 moles of A react with n2 moles of B. The rate of this reaction can be expressed by the rate law equation as, R = k [A]n1 [B]n2 where k is the rate constant of the reaction, hence, the order of the reaction is n = n1 + n2, (observed, experimentally). If n = 1, the reaction is called the first order reaction, if n = 2, it is called the second order reaction, etc. If n = 0, it is called the zero order reaction, e.g. photochemical reaction of H2(g) and Cl2(g).
The features of order of reaction are as follows :
- It represents the number of atoms, ions or molecules whose concentrations influence the rate of the reaction.
- It is not related to the stoichiometric equation of the reaction, hence it cannot be predicted from stoichiometric balanced equation.
- It is experimentally determined quantity.
- It is defined only in terms of the concentrations of the reactants and not of products.
- It may have values which are integers, fractional or zero.
- Higher values are rare. Reactions of first and second order are in large number. Third order reactions are very few like,
2NO(g) + Cl2(g) → 2NoCl(g)
Molecularity of elementary reactions :
- Complex reactions are those which constitute a series of elementary reactions.
- Each step taking place in a complex reaction is called elementary reaction.
- This shows that a complex reaction is broken down in a series of elementary chemical reactions.
- By adding all the elementary steps of a complex reaction we get the overall reaction.
- The mechanism of a reaction is decided from the sequence of the elementary steps that are added to give overall reaction.
Elementary reaction : It is defined as the reaction which takes place in a single step and cannot be divided further into simpler chemical reactions.
The order and molecularity of the elementary reaction are same.
Some reactions take place in one step and cannot be broken down into simpler reactions.
For example,
C2H5I(g) → C2H4(g) + HI(g)
O3(g) → O2(g) + O(g)
Molecularity : The term "molecularity" describes how many molecules of the reactant are involved in a chemical reaction.
Explanation :
- A reaction's molecularity is always present.
- It is impossible to determine experimentally.
- The molecularity has a minimum value of one.
- It is not allowed to have fractional or zero values.
- The reactions are classified according to the molecularity
Reactions are classified based on their molecularity as follows:
(i) Unimolecular reaction (OR First order reaction) : In this only one molecule takes part in the reaction,
Example :
N2O5(g) → 2NO2(g) + ½ O2(g)
The rate law expression for this reaction is,
Rate = k [N205]. Hence it is unimolecular and first order.
Other unimolecular reactions are,
O3(g) → O2(g) + O(g)
C2H5I(g) → C2H4(g) + HI(g)
(ii) Bimolecular reaction : In this two molecules take part in the reaction,
Example :
2HI(g) → H2(g) + I2(g)
O3(g) + O(g) → 2O2(g)
2NO2(g) → 2NO(g) + O2(g)
(iii) Trimolecular reaction : In this three molecules take part in the reaction,
Example :
2NO(g) + O2(g) 2NO2(g)
The higher molecularity is rare since the probability of simultaneous collisions between more molecules is very low.
Order and molecularity of elementary reactions:
The order and molecularity of elementary reaction are same.
Consider the rate law for the elementary reaction
2NO2(g) → 2NO2(g) + O2(g) is found to be rate = k[NO2]2.
The reaction is second order and bimolecular. The order of reaction is 2 and its molecularity is also 2.
Similarly for the elementary reaction,
C2H5I(g) → C2H4(g) + HI(g)
Rate = k[C2H5I]
It is unimolecular and first order.
However the order and molecularity of the reaction may or may not be the same.
Rate determining step :
Many chemical reactions take place in a series of elementary steps. Among many steps of the reaction, one of the steps is the slowest step compared to other steps.
Rate determining step : The slowest step in the reaction mechanism which involves many steps is called rate determining step.
Example : Consider decomposition of gaseous NO2Cl. 2NO2Cl(g) → 2NO2(g) + Cl2(g) This reaction takes place in two steps : Step I : NO2Cl(g) → NO2(g) + Cl(g) …(slow, unimolecular) Step II : NO2Cl(g) + Cl(g) → NO2(g) + Cl2(g) … (fast, bimolecular) -------------------------------------------------------- 2NO2Cl(g) → 2NO2(g) + Cl2(g) (overall reaction) Among two steps, first step being slower represents rate determining step. The rate law can be represented as, Rate = k1 [NO2Cl] Hence, the reaction is first order. In this Cl(g) is formed as a reaction intermediate.
Features of rate determining step :
- The overall reaction rate is determined by the rate determining step.
- The overall reaction will never be faster than the rate determining step.
- The rate determining step can occur anywhere in the reaction mechanism and is determined by the nature of the reactants, reaction conditions, and so on.
- A rate determining step's rate law can be obtained directly from its stoichiometric equation.
Reaction intermediate : The additional species other than the reactants or products formed in the mechanism during progress of the reaction is called reaction intermediate.
Features of reaction intermediate :
- The reaction intermediate appears in the reaction mechanism but does not appear in the overall reaction or in the products.
- It is always formed in one step and consumed in the subsequent step in the mechanism.
- Its concentration is very small and cannot be determined easily.
- Rate of the reaction is independent of concentration of this intermediate.
- The life period of the reaction intermediate is extremely small, hence cannot be isolated.
- The composition of the reaction intermediate, decides the mechanism of the reaction.
- In the above reaction decomposition of gaseous NO2Cl, Cl is formed in the first step and consumed in the second. Such species represents the reaction intermediate.
- The concentration of reaction intermediate does not appear in the rate law.
Distinguish between order and molecularity of a reaction :
Order
Molecularity
It is experimentally determined property.
It is theoretical entity.
It is the sum of powers of the concentration terms of reactants those appear in the rate equation.
It is the number of reactant molecules taking part in an elementary reaction.
It may be an integer, fraction or zero.
It is integer.
It is the property of elementary and complex reactions.
It is the property of elementary reactions only.
Rate law expression describes the order of the reaction.
Rate law does not describe molecularily.
We reply to valid query.