Notes-Part-1
|
Topics to be Learn : Part-1
|
Introduction :
Electrolytes : The substances which in their aqueous solutions (or in any polar solvents) dissociate or ionise forming positively charged ions (cations) and negatively charged ions (anions) are called electrolytes. For example, NaCl, HCI, etc.
Ionic equilibrium : The equilibrium between ions and unionised molecules of an electrolyte in solution is called an ionic equilibrium.
CH3COOH(aq) ⇌ CH3COO-(aq) + H+(aq).
Types of electrolytes :
Strong electrolytes : The electrolytes which ionize completely or almost completely are called strong electrolytes.
- Examples : NaCl, HCl, H2SO4, CH3COONH4 , AgCl, CuSO4,etc.
Weak electrolytes : The electrolytes which dissociate to a less extent are called weak electrolytes.
- Examples: CH3COOH, NH4OH, etc.
Degree of dissociation (∝) :
Degree of dissociation : It is defined as a fraction of total number of moles of an electrolyte that dissociate into its ions at equilibrium. It is denoted by symbol ∝ and given by
α = \(\frac{\text{Number of moles dissociated}}{\text{Total number of moles}}\)
Percent dissociation = α × 100
If 'c' is the molar concentration of an electrolyte the equilibrium concentration of cation or anion is (α × c) mol dm-3.
Acids and Bases :
Arrhenius theory of acids and bases :
According to this theory acids and bases are defined as follows :
Acid : Acid is a substance which contains hydrogen and gives rise to H+ ions in aqueous solution.
For example :
HCl (aq) → H+(aq) + Cl−(aq)
CH3COOH(aq) \(\overset{water}{\leftrightarrow}\)CH3COO (aq)+ H+(aq)
Base : A substance that contains OH group and produces hydroxide ions (OH−) in aqueous solution is called a base. E.g. NaOH
NaOH(aq) → Na+(aq) + OH−(aq) .
NH4OH(aq) ⇌ NH4+(aq) + OH−(aq)
Limitations of Arrhenius theory :
- This theory is applicable only for aqueous solutions and not for non-aqueous solutions.
- It fails to explain the acidic nature of non-hydrogen compounds like BF3, AlCl3, FeCl3, etc.
- It fails to explain the basic nature of non-hydroxy compounds like NH3, amines, Na2CO3, KCN, aniline, etc. in their aqueous solutions.
- It does not explain role of solvent or existence of H3O+ in an aqueous solution of an acid.
Neutralisation reaction : According to Arrhenius theory, neutralisation is a reaction between an acid and a base in their aqueous solutions producing salt and unionised water.
HCl(aq) + NaOH(aq) -—> NaCl(aq) + H2O(l)
Since strong acid, strong base and salt dissociate completely, the above reaction is represented as,
H+(aq) + Cl(aq) + Na+(aq) + OH−(aq) -—>Na+ (aq) + Cl−(aq) + H2O(l)
OR
H+(aq) + OH−(aq) -—> H2O(l)
Hence, according to Arrhenius theory neutralisation reaction is defined as a reaction between H+ ions and OH− ions forming unionized water molecules.
Bronsted - Lowry theory : J. N. Bronsted and T. M. Lowry (1923) proposed a more general theory known as the Bronsted-Lowry proton transfer theory.
According to this theory
Acid : Acid is a substance that donates a proton (H+) to another substance.
Base : Base is a substance that accepts a proton (H+) from another substance.
For example,
HCl(aq) + NH3(aq) ⇌ NH4+ + Cl−(aq))
Acid Base
Since HCl donates a proton it is an acid while NH3 accepts a proton it is a base.
| Know this :
Hydrochloric acid, HCl present in the gastric juice is secreted by our stomach and is essential for digestion of food. |
Conjugate acid-base pair :
The base produced by accepting the proton from an acid is the conjugate base of that acid. Likewise the acid produced when a base accepts a proton is called the conjugate acid of that base.
A pair of an acid and a base differing by a proton is called a conjugate acid-base pair.
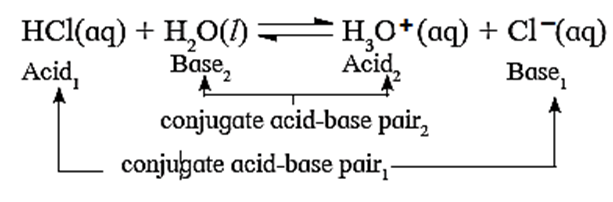
Q. Identify conjugate acid-base pairs in the following.
(a) NH4+ + OH- ⇌ NH3 + H2O
(b) HCO3- + H2O ⇌ H3O+ + CO32-
(C) NH4+ + H2O ⇌ H3O+ + NH3
(d) HNO3 + H2O ⇌ H3O+ + NO3-
| Acid | Base | Conjugate base | Conjugate acid | |
| NH4+ + OH- ⇌ NH3 + H2O | NH4+ | OH | NH3 | H2O |
| HCO3- + H2O ⇌ H3O+ + CO32-
|
HCO3- | H2O | CO32- | H3O+ |
| NH4+ + H2O ⇌ H3O+ + NH3 | NH4+ | H2O | NH3 | H3O+ |
| HNO3 + H2O ⇌ H3O+ + NO3- | HNO3 | H2O | NO3- | H3O+ |
Lewis theory :
Lewis theory is based on the electron theory
According to this theory acids and bases are defined as follows.
Acid : Any species that accepts a share in an electron pair is called Lewis acid.
- E.g. BF3, AlCl3 and all electron deficient species like cations (K+, Ag+) and molecules having incomplete octet, like BeF2, BF3.
- Since cations are deficient of electrons they accept a pair of electrons, hence they are Lewis acids.
Base : Any species that donates a share in an electron pair is called Lewis base.
- E.g. NH3, C2H5NH2 and all electron rich species like anions (Cl-, OH-) and all molecules with lone pair of electrons.
Lewis theory explanation with examples :
(A) According to Lewis theory, an acid is a substance which can accept a pair of electrons.
In BF3 molecule, the octet of B is incomplete, hence it needs two electrons or a pair of electrons to complete its octet. Hence BF3 acts as a Lewis acid.
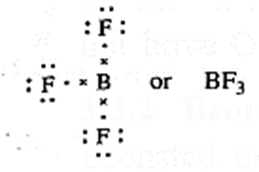
(B) According to Lewis theory, a base is a substance which can donate a pair of electrons.
In NH3 molecule, nitrogen atom has one lone pair of elctrons to donate.
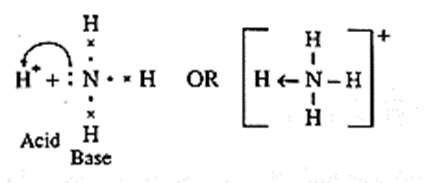
Hence NH3 acts as a Lewis base. The reaction between BF3 and NH3 can be represented as,
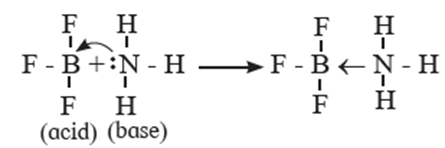
Amphoteric nature of water : Water has the ability to act as an acid as well as a base. Such behaviour is known as amphoteric nature of water.
For example :
Acid : H2O(l) + NH3(aq) ⇌ OH-(aq) + NH4+(aq)
Base : H2O(l) + HCl(aq) ⇌ H3O+(aq) + Cl-(aq)
H2O acts as an acid towards NH3 and as a base towards HCl. Therefore H2O is amphoteric.
Q. All Bronsted bases are also Lewis bases, but all Bronsted acids are not Lewis acids. Explain.
(1) NH3 is a Bronsted base since it can accept a proton while it is also a Lewis base since it has a lone pair of electrons to donate.
Bronsted base : NH3 + H+ —> NH4+
Lewis base : H + : NH3 —> NH4+
(2) HCI is a Bronsted acid since it can donate a proton but it is not a Lewis acid since it can’t accept a pair of electrons.
Bronsted acid : HCl + H2O —> H3O+ + Cl-
Ionisation of acids and bases :
On the basis of extent of dissociation, acids and bases are classified as follows :
Strong acids and strong bases : The acids and bases which dissociate to a greater extent or almost completely are called strong acids and strong bases.
HCl (aq) —> H+(aq) + Cl-(aq)
NaOH(aq) —> Na+(aq) + OH-(aq)
Weak acids and weak bases : The acids and bases which dissociate partially are called weak acids and weak bases. There exists an equilibrium between undissociated molecules and ions in solution.
CH3COOH(aq) ⇌ CH3COO-(aq) + H+(aq)
NH4OH(aq) ⇌ NH4+(aq) + OH-(aq)
Examples of (a) strong acids and strong bases, (b) weak acids and bases.
- Strong acids : HCl, H2SO4
- Strong bases : NaOH, KOH
- Weak acids : HCOOH, CH3COOH
- Weak bases : NH4OH, C2H5NH2
Dissociation constant of a weak acid : It is defined as the equilibrium constant for dissociation equilibrium of a weak acid and denoted by Ka.
Explanation : Consider an aqueous solution of a weak acid HA.
HA(aq) ⇌ H+(aq) + A-(aq)
The equilibrium constant called dissociation constant Ka is represented as,
Ka = \(\frac{[H^+]×[A^-]}{[HA]}\)
Dissociation constant of a weak base : It is defined as the equilibrium constant for dissociation equilibrium of a weak base and denoted by Kb.
Explanation : Consider an aqueous solution of a weak base BOH.
BOH(aq) ⇌ B+(aq) + OH-(aq)
The equilibrium constant called dissociation constant, Kb is represented as,
Kb = \(\frac{[B^+]×[OH^-]}{[BOH]}\)
Expression of Ostwald’s dilution law in the case of a weak electrolyte : Consider the dissociation of a weak electrolyte BA. Let V dm3 of a solution contain one mole of the electrolyte.
Then the concentration of a solution is, C = 1/V mol dm−3
Let α be the degree of dissociation of the electrolyte,
| BA ⇌ B+ + A | |||
| Initial moles : | 1 | 0 | 0 |
| Moles of equilibrium : | 1− α | α | α |
| Concentration at equilibrium (mol dm−3) | (1− α)/V | α /V | α /V |
Applying the law of mass action to this dissociation equilibrium, we have,
K = \(\frac{[B^+]×[A^-]}{[BA]}\)
∴ K = \(\frac{(α /V)×(α /V)}{(1-α) /V}= \frac{α^2}{(1-α)V\)
As the electrolyte is weak, ∝ is very small as compared to unity,
(1 — α) ≈ 1.
∴ K = \(\frac{α^2}{V}\)
∴ α = \(\sqrt{KV}\)
∴ α ∝ \(\sqrt{V}\)
1/V = C, where C = concentration in mol dm−3
∴ K = α2C
∴ α = \(\sqrt{\frac KC}\)
∴ α = \(\sqrt{KV}\) (‘ .’ C = 1/V or V = 1/C)
∴ α = \(\sqrt{\frac KC}\)
This is the expression of Ostwald’s dilution law. Thus, the degree of dissociation of a weak electrolyte is directly proportional to the square root of the volume of the solution containing 1 mole of an electrolyte.
Expression of Ostwald’s dilution law in case of a weak acid :
Consider the dissociation of a weak acid HA. Let V dm3 of a solution contain one mole of weak acid HA.
Then the concentration of a solution is, C = 1/V mol dm−3
Let α be the degree of dissociation of HA,
| HA ⇌ H+ + A- | |||
| Initial moles : | 1 | 0 | 0 |
| Moles of equilibrium : | 1− α | α | α |
| Concentration at equilibrium (mol dm−3) | (1− α)/V | α /V | α/V |
Applying the law of mass action to this dissociation equilibrium, we have,
Ka = \(\frac{[H^+]×[A^-]}{[HA]}\)
∴ Ka = \(\frac{(α /V)×(α /V)}{(1-α) /V}= \frac{α^2}{(1-α)V\)
As the electrolyte is weak, ∝ is very small as compared to unity,
(1 — α) ≈ 1.
∴ Ka = \(\frac{α^2}{V}\)
∴ α = \(\sqrt{K_aV}\)
∴ α ∝ \(\sqrt{V}\)
‘.’ C= 1/V
∴ α = \(\sqrt{\frac{K_a}{C}}\)
This is the expression of Ostwald’s dilution law. Thus, the degree of dissociation of a weak acid is directly proportional to the square root of the volume of the solution containing 1 mole of acid or inversely proportional to square root of its concentration.
Expression of Ostwald’s dilution law in case of a weak base :
Consider the dissociation of a weak base BOH. Let V dm3 of a solution contain one mole of weak base BOH.
Then the concentration of a solution is, C = 1/V mol dm−3
Let α be the degree of dissociation of BOH,
| BOH ⇌ B+ + OH- | |||
| Initial moles : | 1 | 0 | 0 |
| Moles of equilibrium : | 1− α | α | α |
| Concentration at equilibrium (mol dm−3) | (1− α)/V | α /V | α/V |
Applying the law of mass action to this dissociation equilibrium, we have,
Kb = \(\frac{[B^+]×[OH^-]}{[BOH]}\)
∴ Kb = \(\frac{(α /V)×(α /V)}{(1-α) /V}= \frac{α^2}{(1-α)V\)
As the electrolyte is weak, ∝ is very small as compared to unity,
(1 — α) ≈ 1.
∴ Kb = \(\frac{α^2}{V}\)
∴ α = \(\sqrt{K_bV}\)
∴ α ∝ \(\sqrt{V}\)
‘.’ C= 1/V
∴ Kb = α2C
∴ α = \(\sqrt{\frac{K_b}{C}}\)
∴ α ∝ \(\sqrt{\frac{1}{C}}\)
This is an expression of Ostwald’s dilution law. Thus, the degree of dissociation of a weak base is directly proportional to the square root of the volume of the solution containing one mole of a base or inversely proportional to the square root of its concentration.
Autoionisation of water :
Pure water ionises to a very less extent. The ionisation equilibrium is represented as follows :
H2O(l) + H2O(l) ⇌ H3O+(aq) + OH−(aq)
The equilibrium constant K for the above equilibrium is represented as,
K = \(\frac{[H_3O^+]×[OH^-]}{[H_2O]^2}\)
∴ K x [H2O]2 = [H3O+] x [OH−]
Since K and active mass of pure water [H2O] are constant we can write,
K x [H2O] = Kw
∴ Kw = [H3O+] x [OH−]
where Kw is called ionic product of water. At 25 0C
KW = 1 x 10−14.
We reply to valid query.