Solutions
Maharashtra Board-Class-12-Chemistry-Chapter-2
Notes-Part-1
|
Topics to be Learn : Part-1
|
Introduction :
Solution : The solution is a homogeneous mixture of two or more components or pure substances.
- When the size of particles of the components is of the order of 10-10 m, then the solution is called a true solution.
- E.g. An aqueous solution of sugar.
Solvent : The component in which solution formation takes place and which constitutes larger proportion of a solution is called solvent. For example, in an aqueous solution of sugar, water is the solvent.
Solute : In a solution, the component which dissolves and constitutes smaller proportion of a solution is called a solute. For example, in a sugar Solution, sugar is the solute.
Types of solutions :
Homogeneous solution : A solution in which solute and solvent form uniform homogeneous one phase due to attraction between their molecules/particles is called homogeneous solution.
- E.g. A solution of NaCl or sugar.
Heterogeneous solution : A solution consisting of two or more phases is called a heterogeneous solution.
- E.g. A colloidal solution of starch.
A solution consists of a solvent and a solute. Since the physical states of a solvent and a solute may be gaseous, liquid or a solid, there are nine types of solutions.
| Types of solutions | State of solute | State of solvent | Examples |
| Solid in Liquid | Solid | Liquid | Sea water, benzoic acid in benzene, sugar in water |
| Solid in solid | Solid | Solid | Metal alloys such as brass, bronze. |
| Solid in Gas | Solid | Gas | Iodine in air, Smoke |
| Liquid in Liquid | Liquid | Liquid | Gasoline, ethanol in water. |
| Liquid in solid | Liquid | Solid | Amalgams of mercury with metals as mercury in silver |
| Liquid in Gas | Liquid | Gas | Chloroform in nitrogen, Moisture |
| Gas in Liquid | Gas | Liquid | Carbonated water (CO2 in water- Soda water), oxygen in water. |
| Gas in solid | Gas | Solid | H2 in palladium |
| Gas in Gas | Gas | Gas | Air (O2, N2, Ar and other gases) |
Capacity of a solution to dissolve a solute :
Saturated solution : A solution which contains maximum amount of solute dissolved in a given amount of solvent at a given temperature, further the solute can’t be dissolved is called a saturated solution.
There exists a dynamic equilibrium where the number of solute molecules leaving the crystal to pass into solution is equal to the number returning from the solution to the crystal. Which is represented as,
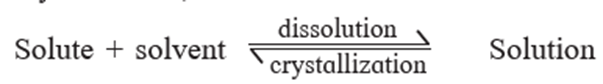
Supersaturated solution : A solution containing a solute more than that required to form a saturated solution at equilibrium is called a supersaturated solution.
When a tiny crystal of a solute is added to supersaturated solution, the excess solute separates out and forms saturated solution.
Solubility : The solubility of a solute is its amount per unit volume of saturated solution at a specific temperature.
The solubility of a solute is its maximum concentration and expressed in the concentration units mol L-1.
Factors on which the solubility of a substance (solute) depends :
The extent of dissolution of a substance (solute) depends upon the following factors
- Nature of a solute : A solute may be crystalline, amorphous, ionic or covalent. Hence accordingly its tendency to dissolve changes. The substances having similar intermolecular forces tend to dissolve in each other.
- Nature of solvents : Solvents are classified as polar and nonpolar. Polar solutes dissolve in polar solvents. For example, ionic compounds dissolve in polar solvent like water. A solvent other than water is called a non-aqueous solvent. For example, C6H6, CCl4, etc. Solutions in these solvents are called nonaqueous solutions. The solvent may be a gas, a liquid or a solid.
- Amount of a solvent : More amount of a solvent will dissolve more quantity of the solute.
- Temperature : Depending on the nature of a solvent and a solute the solubility changes with temperature. The effect depends on the heat of solution, hydration energy, etc. Generally as the temperature increases, solubility of solid increases and that of gases decreases.
- Pressure : Pressure has no effect on the solubilities of solids and liquids since they are incompressible. The effect of pressure is important only for solutions which involve gases as solute. With the increase in pressure and decrease in temperature, the solubility of gases increases.
Le Chatelier’s principle the effect of temperature on solubility :
- The effect of temperature on solubility depends on enthalpy of solution.
- For example, dissolution of KCl in water is an endothermic process since heat is absorbed during dissolution. In this according to Le Chatelier’s principle by increasing temperature the solubility of KCl increases.
- Dissolution of CaCl2, Li2SO4, H2O in water is an exothermic process since heat is evolved during dissolution. In this, according to Le Chatelier’s principle by increasing the temperature the solubility decreases.
Q. Why naphthalene dissolves in benzene but not in water ?
Since naphthalene is a covalent non-polar substance’ it is soluble in a non-polar solvent like benzene but insoluble in polar solvent like water.
Q. Anhydrous sodium sulphate dissolves in water with the evolution of heat. What is the effect of temperature on its solubility ?
Since the dissolution of anhydrous sodium sulphate in water is an exothermic process due to evolution of heat, according to Le Chatelier’s principle its solubility decreases with the increase in temperature.
Solubility of gases in liquids :
- Gases are soluble in water and other liquids and their solubility depends upon the nature of the gas.
- Non-polar gases like O2, have less solubility in polar solvents.
- Polar gases like CO2, NH3, HCl, etc. are more Soluble in polar solvent like water. CO2 forms H2CO3, while NH3 forms NH4OH in aqueous solutions.
- The solubility of gases in liquids increases with the increase in pressure and the decrease in temperature.
Effects of temperature on solubility of a gas in water :
- The gases are soluble in water and other liquids.
- According to Charles’ law, the volume of a given mass of a gas increases with the increase in temperature at constant pressure.
- Hence, the volume of the dissolved gas increases with the increase in temperature.
- This enormous increase in volume of the gases cannot be accommodated by the solvent molecules, hence excess of the gases escape out in the form of bubbles.
- Therefore, the solubility of gases in liquids decreases with temperature.
Henry’s law (Effect of pressure on the solubility of the gases) :
Since the gases are compressible, their solubility in the liquids is influenced by external pressure of the gas. The solubility of gases increases with the increase in pressure.
Henry’s law states that the solubility of a gas in a liquid at constant temperature is proportional to the pressure of the gas above the solution.
- If S is the solubility of a gas in mol dm-3 at a pressure P and constant temperature then by Henry’s law,
- S ∝ P or S = KH x P , where KH is called Henry’s law constant.
- If P = 1 atm, then S = KH.
- If several gases are present, then the solubility of any gas in the mixture is proportional to its partial pressure at given temperature.
Illustration of Henry’s law : In case of aerated or carbonated drink beverage, the bottle is filled by dissolving CO2 gas at high pressure and then sealed.
- Above the liquid surface there is air and undissolved CO2. Due to high pressure, the amount of dissolved CO2 is large.
- When the cap of the aerated bottle is removed, the pressure on the solution is lowered, hence excess of CO2 and air escape out in the form of effervescence. Thus by decreasing the pressure, solubility of CO2 is decreased.
Exceptions to Henry's law :
The gases like NH3 and CO2 do not obey Henry’s law. This is because, these gases react with water,
- NH3(g) + H2O(l) --> NH4+(aq) + OH-(aq)
- CO2(g) + H2O(l) —> H2CO3(aq)
Due to reactions of the gases like NH3, CO2(g), they have higher solubility than expected by Henry’s law.
Units of Henry’s law constant :
By Henry’s law, S = KH x R where S is solubility of the gas in mol dm-3, P is the pressure of the gas in atmosphere (or in bar) and KH is Henry’s law constant.
S(mol dm-3)
KH = \(\frac{S^{(mol/dm^3)}}{P_{atm}}\) mol dm-3 atm-1 or mol dm-3 bar-1
Hence the units of Henry’s law constant KH are mol dm-3 atm-1
Q. Why Oxygen gas is slightly soluble in water but it is highly soluble in blood.
The O2 gas has very low solubility in water. However, its solubility in blood is exceedingly high. This is because of binding of O2 molecule to haemoglobin present in blood. Haemoglobin is a vital constituent of blood, reacts with oxygen increasing the solubility of oxygen.
Haemoglobin + 4O2(g) —> Haemoglobin O8
This oxygenated blood is circulated to various parts of the body, for the supply of oxygen.
Q. Explain, why do aquatic animals prefer to stay at lower level of water during summer ?
The solubility of oxygen gas decreases with the increase in temperature.
In sea or lake water, the temperature of upper level is higher than the lower level.
Therefore the dissolved oxygen content in water is more at lower level than at higher level required for the marine life.
Hence marine life like fish prefers to stay at lower level than upper level of water.
Vapour pressure of solutions of liquids in liquids :
Raoult’s law : The law states that, at constant temperature, the partial vapour pressure of any volatile component of a solution is equal to the product of vapour pressure of the pure component and the mole fraction of that component in the solution.
Suppose that for a binary solution of two volatile liquids A1 and A2,
P1 and P2 are their partial vapour pressures
x1 and x2 are their mole fractions in solution.
Then according to Raoult’s law,
we write P1 = x1P01 and P2 = x2P02 ….. (1)
where P01 and P02 are vapour pressures of pure liquids A1 and A2, respectively.
According to Dalton’s law of partial pressures, the total pressure P above the solution is,
PT = P1 + P2 = x1P01 + x2P02 ……(2)
Since x1 + x2 = 1 \ x1 = 1- x2, the Eq. (1) can also be written as
\ PT = (1- x2) P01 + x2P02
= P01 - x2P01 + x2P02
= (P02 - P01) x2 + P01 ….. (3)
With the help of above equation, the vapour pressures of solutions having different concentrations (or mole fractions) can be calculated.
Variation of vapour pressure with mole fraction of a solute in a liquid mixture :
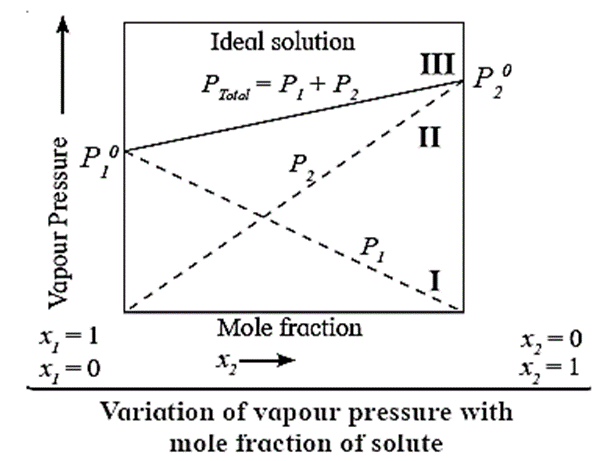
Because P01 and P02 are constants, a plot of PT versus x2 is a straight line as shown in the Fig The figure also shows the plots of P1 versus x1 and P2 versus x2 according to the equations 1. These are straight lines passing through origin.
When x1= 1, x2=0, PT = P01 and when x1=0, x2 = 1, PT = P02 as shown by lines I and II in Fig.
Composition of vapour phase above a liquid mixture.
Consider a liquid mixture of two liquids A and B having vapour pressures P0A and P0B and mole fractions x1 and x2 respectively in the liquid phase.
By Raoult’s law, the vapour pressures of two liquids will be,
PA = x1 P0A and PB = x2 P0B
The total vapour pressure of this liquid mixture is,
PT = PA + PB
Pr = x1P0A + x2P0B
The vapour above liquid surface contains A and B.
If y1 and y2 are the mole fractions of A and B components respectively in the vapour phase, then by Dalton’s law of partial pressures,
PA = y1PT and PB = y2PT
and total vapour pressure is,
PT =y1PT + y2PT
Ideal solutions : These are solutions which obey Raoult’s law over an entire range of concentrations at constant temperature.
- Example : A liquid mixture of benzene and toluene which have nearly identical physical properties and intermolecular forces forms an ideal solution.
Characteristics of ideal solutions :
- The ideal solutions obey Raoult’s law over entire range of concentrations at constant temperature.
- In the formation of an ideal solution, heat is neither evolved nor absorbed and enthalpy change for mixing is zero, i.e. ΔmixH = 0.
- In the formation of an ideal solution, there is no volume change on mixing two liquid components and the volume of solution is equal to the sum of volumes of two liquid components. ΔmixV = 0
- In the ideal solution, solvent-solvent, solute-solute and solvent-solute interactions are comparable.
- The vapour pressure of an ideal solution lies between vapour pressures of two pure components.
Nonideal solutions : These are solutions which do not obey Raoult’s law over the entire range of concentrations.
Characteristics of nonideal solutions :
- Nonideal solutions do not obey Raoult’s law over the entire range of concentrations.
- The vapour pressures of these solutions may be higher or lower than ideal solutions.
- These solutions exhibit two types of deviations from Raoult’s law namely (a) positive deviation and (b) negative deviation.
- These solutions give azeotropic mixtures.
Solutions with positive deviations from Raoult’s law :
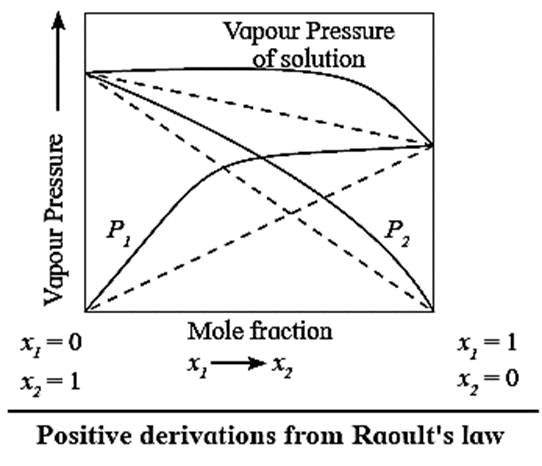
- A solution or a liquid mixture which has higher vapour pressure than theoretically calculated by Raoult’s law or higher than those of pure components is called a nonideal solution with positive deviation.
- In these solutions, solute-solvent intermolecular attractions are weaker than those between solvent-solvent and solute-solute interactions.
- For example, solutions of acetone and ethanol, carbon disulphide and acetone, etc.
Solutions with negative deviations from Raoult’s law :

- A solution or a liquid mixture which has lower vapour pressure than theoretically calculated by Raoult’s law or lower than those of pure components is called a nonideal solution with negative deviation.
- In these solutions, the intermolecular interactions between solvent and solute molecules are stronger than solvent-solvent or solute-solute interactions.
- For example, solutions of phenol and aniline, chloroform and acetone, etc.
Colligative properties of nonelectrolyte solutions :
Colligative Property : The property of a solution which depends on the total number of particles of the solute (molecules, ions) present in the solution and does not depend on the nature or chemical composition of solute particles is called colligative property of the solution.
Examples of colligative properties :
- lowering or relative lowering of vapour pressure of a solution
- elevation in the boiling point
- depression in the freezing point
- osmotic pressure.
Vapour pressure of a liquid :
- If a volatile liquid is placed in an open vessel, the liquid molecules have a tendency to escape in a gaseous state forming vapour and diffuse into surroundings. Hence evaporation takes place continuously and no equilibrium is attained.
- If a liquid is placed in a closed vessel, the vapour molecules get accumulated on its surface. These vapour molecules are in continuous random motion. They collide with each other, with walls of a container and surface of the liquid, and return to the liquid state. This reverse phenomenon is called condensation.
- After some time, rates of evaporation and condensation become equal and an equilibrium is established between liquid and vapour phases. At this stage the vapour exerts a constant pressure called vapour pressure on liquid surface at constant temperature.
- Vapour pressure: The pressure exerted by the vapour of a liquid (or solid) when it is in equilibrium with the liquid (or solid) phase at a constant temperature is called the vapour pressure of the liquid (or solid).
- The vapour pressure of a liquid increases with the increase in temperature.
Relative vapour pressure of a solution : If P0 is the vapour pressure of a pure liquid (solvent) and P is the vapour pressure of a solution after adding a nonvolatile solute, then, relative vapour pressure P = P/P0
Lowering of vapour pressure of a solution : When a nonvolatile solute is added to a pure solvent, the surface area is covered by the solute molecule decreasing the rate of evaporation, hence its vapour pressure decreases. This decrease in vapour pressure is called lowering of vapour pressure.
- If P0 is the vapour pressure of a pure solvent (liquid) and P is the vapour pressure of the solution, where P < P0, then, (P0 — P) is the lowering of the vapour pressure.
Relative lowering of vapour pressure : If Po and P are the respective vapour pressures of a pure liquid (solvent) and the solution containing a nonvolatile solute
then P < P0. Hence, P0 — P represents the lowering of the vapour pressure due to addition of a nonvolatile solute.
Relative lowering of vapour pressure = \(\frac{P_0-P}{P_0}=\frac{ΔP}{P_0}\)
Raoult’s law for solutions of nonvolatile solutes :
Statement of Raoult’s law : The law states that the vapour pressure of a solvent over the solution of a nonvolatile solute is equal to the vapour pressure of the pure solvent multiplied by mole fraction of the solvent at constant temperature.
Explanation : Let P0 and P be the vapour pressures of a pure solvent and a solution respectively. If x1 is the mole fraction of the solvent then Raoult’s law can be represented as, P = x1P0
For a binary solution containing one solute, if x1 and x2 are mole fractions of a solvent and a solute respectively then,
x1 + x2 = 1
x1 = 1 - x2
P = x1P0
= (1 - x2)P0
= P0 - x2P0
P0 - P = x2P0
∴ x2 = \(\frac{P_0-P}{P_0}\)
P0 - P = ΔP is the lowering of vapour pressure
∴ x2 = \(\frac{ΔP}{P_0}\)
In the equation, is called relative lowering of vapour pressure.
Hence Raoult’s law can also be stated as the relative lowering of vapour pressure is equal to mole fraction of the solute.
Q. Show that relative lowering of vapour pressure is a colligative property.
Consider a binary solution containing a nonvolatile solute. If P0 and P are vapour pressures of a pure solvent and the solution respectively then, Lowering of vapour pressure = ΔP = P0 - P
Relative lowering of vapour presure = \(\frac{P_0-P}{P_0}\)
By Raoult’s law,
x2 = \(\frac{P_0-P}{P_0}\)
where x2 is mole fraction of the solute. Therefore the relative lowering of vapour pressure is a colligative property.
Variation of vapour pressure with mole fraction of a solvent in solution. OR
Variation of vapour pressure with the concentration of a solution :
The vapour pressure of a pure solvent decreases when a nonvolatile solute is dissolved in it.
Consider a pure solvent with vapour pressure P0 and mole fraction x1.
For a solution containing a nonvolatile solute, if x1 and x2 are the mole fractions of a solvent and a solute respectively, then x1 + x2 = 1 and x1 < 1.
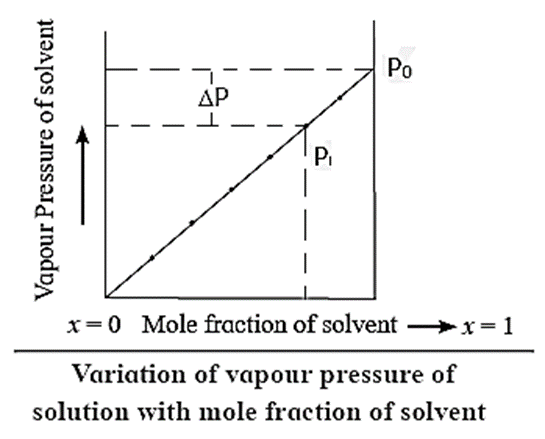
By Raoult’s law, P = x1P0. As the mole fraction of a solvent in the solution increases the vapour pressure increases as shown in the above Fig. When x1 becomes equal to 1, the vapour pressure becomes P0, ie the vapour pressure of a pure solvent.
If at any mole fraction of a solvent, the vapour of the solution is P, then the lowering of vapour pressure will be, ΔP = P0 - P.
Relation between relative lowering of vapour pressure and molar mass of nonvolatile solute :
Consider a solution in which W1 gram of a solvent of molar mass (or molecular weight) M1 contains W2 gram of a solute of molar mass M2.
Then number of moles of a solvent = n1 = W1/ M1
Number of moles of a solute = n2 = W2/ M2
Total number of moles = n = n1 + n2
Mole fraction of the solvent = x1 = n1/n
Mole fraction of the solute = x2 = n2/n
∴ x1 + x2 = \(\frac{n_1}{n}+\frac{n_2}{n}\)=\(\frac{n_1+n_2}{n}=\frac{n}{n} =1\)
∴ x1 + x2 =1
In the case of an ideal solution which is a dilute solution, the concentration and the number of moles of the solute are very low, i.e. n2 << n1
∴ n1 + n2 ≅ n1
Now x2 = n2/n = \(\frac{n_2}{n_1+n_2}≅ \frac{n_2}{n_1}\)
∴ x2 = \(\frac{W_2/M_2}{W_1/M_1}\)= \(\frac{W_2M_1}{W_1M_2}\)
If P0 and P are the vapour pressures of a pure solvent and a solution respectively, then
relative lowering of vapour pressure = \(\frac{P_0-P}{P_0}\)
By Raoult’s law,
\(\frac{ΔP}{P_0}\)=\(\frac{P_0-P}{P_0}\) = x2
∴\(\frac{P_0-P}{P_0}\)=\(\frac{W_2M_1}{W_1M_2}\)
or
\(\frac{ΔP}{P_0}\)=\(\frac{W_2M_1}{W_1M_2}\)
Hence by measuring the vapour pressure of a pure solvent and a solution, the molar mass of the dissolved nonvolatile substances can be determined. .
PDF : Class-12-Chemistry-Chapter-2-Solutions-Text Book
PDF : Class-12-Chemistry-Chapter-2-Solutions- Notes
PDF : Class-12-Chemistry-Chapter-2-Solutions- Solution
All 16 Chapters Notes -Class-12-Chemistry (16-PDF)
All 16 Chapters Solutions -Class-12-Chemistry (16-PDF)
All 16 Chapters Notes+Solutions -Class-12-Chemistry (32-PDF)
Main Page : – Maharashtra Board Class 12th-Chemistry – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter-1-Solid State – Online Notes
Next Chapter : Chapter-3-Ionic Equilibria – Online Notes
Very important note