Solid State
Maharashtra Board-Class-12-Chemistry-Chapter-1
Notes-Part-1
|
Topics to be Learn : Part-1
|
Physical states of matter : There are three physical states of matter namely solid, liquid and gas.
- They differ in intermolecular or interatomic or interionic forces which are strongest in the solid state.
- By raising the temperature of solids to their melting point, solids are converted into liquids while heating liquids to their boiling points, they can be converted into vapour or gaseous state. (Solid Liquid Gas )
- On the contrary, by cooling the gases to very low temperature and subjecting to high pressure they can be transformed into liquid which on further cooling can be transformed into solid state. Gas Liquid Solid
The equilibrium existing between three states of matter may be represented as,

Constituents of solids : The smallest constituent particles of various solids are atoms, ions or molecules. All such small constituents are referred to as ‘particles’.
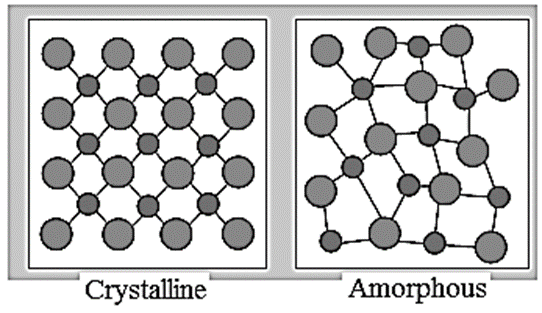
Types of solids : Depending on orderly arrangement of the constituent particles, the solids are classified into two types :
- Crystalline solid : A homogeneous solid in which the constituent particles like atoms, ions or molecules are arranged in a definite repeating pattern throughout the solid is called crystalline solid. Examples: NaCl, KNO3, etc.
- Amorphous solid : A substance which appears like solid but does not have perfectly ordered crystalline structure and no regular arrangement of constituent particles in structure is called amorphous solid. Examples: glass, rubber, plastics, etc.
Characteristic properties of solids :
- The solid state of matter is characterised by strong interparticle forces of attraction.
- There is regularity and periodicity in the arrangement of constituent particles of solid.
- Generally solids are hard, incompressible and rigid except some solids like Na, K, P which are soft.
- The constituent particles of solids like molecules, atoms or ions have fixed stationary positions in solid and can only oscillate about their equilibrium or mean positions. Hence, they have fixed shape and cannot be poured like liquids.
- Crystalline solids have sharp melting points and they melt at a definite temperature. Amorphous solids do not have sharp melting points.
- All crystalline substances except those having cubic structure are anisotropic. Their properties like refractive index, thermal and electrical conductivity, etc, are different in different directions. They are anisotropic or isotropic.
Anisotropy : The ability of crystalline solids to change their physical properties when measured in different directions is called anisotropy.
Explanation : This property is due to different arrangement of constituents in different directions. Different types of particles fall on the way of measurements in different directions. Hence the composition of crystalline solid changes with directions changing their physical properties.

Fig. Anisotropy in crystals : Different arrangements of constituent particles about different directions, AB, CD and EF.
The two types of circles in this figure represent two types of constituent particles of a solid.
The arrangement of particles in this solid is regular.
- represents arrangement of identical particles of one type.
- represents arrangement of identical particles of another type.
- represents regular arrangement of two different particles in alternate positions.
| Remember :
• A single crystal has ordered (regular and periodic) arrangement of constituent particles throughout its bulk. • Majority of crystalline solids, including metals, are polycrystalline in nature. Single granule of a polycrystalline solid is made of many single crystals or crystallites packed together with different orientations. • Single crystals are difficult to obtain. Diamond is an example of naturally formed single crystal. |
Isotropy : The ability of amorphous solids to exhibit identical physical properties even though measured in different directions is called isotropy.
Explanation : This property arises because there is no long range order of regular pattern of arrangement in them and hence the arrangement is irregular along all the directions. Therefore the magnitude of any physical property would be identical along all directions.
Q. Why does crystalline solid show different refractive indices in different directions ?
Crystalline solid has long range order of regular pattern of arrangement which repeats periodically over entire crystal.
Within the given pattern, the arrangements of different atoms or ions or molecules is different in different directions. Hence the properties like refractive indices in the different directions are different.
This shows that the crystalline solids are anisotropic in nature.
Properties of amorphous solids :
- The constituent particles in amorphous solids are arranged randomly.
- They have short range ordered structure.
- Amorphous solids are called supercooled liquids having very high viscosity.
- They do not have sharp melting points and they melt gradually over a temperature interval.
- Amorphous substances appear like solids but they do not have perfectly ordered crystalline stmcture, hence they are not real solids. Therefore they are pseudo solids.
- They are isotropic and exhibit the same magnitude of any property in every direction.
- Glass, plastic, rubber, tar, and metallic glass (metal-metalloid alloy) are a few examples of amorphous solids.
lsomorphism : A phenomenon in which two or more crystalline substances show same crystalline structure is called isomorphism and the crystals are said to be isomorphous. For example, NaNO3 and CaCO3. They have atomic ratios 1 : 1 : 3.
Polymorphism : A single substance that exists in two or more forms or crystalline structures is said to be polymorphous.
- Polymorphs of a substance are formed under different conditions. For example: Calcite and aragonite are two forms of calcium carbonate, α-quartz, b-quartz and cristobalite CsNO3 are three of the several forms of silica.
- Polymorphism occuring in elements is called allotropy. For example: three polymorphic (allotropic) forms of carbon are diamond, graphite and fullerene.
Q. Why does a crystalline solid has a sharp melting point ?
- Crystalline solid is a homogeneous solid and it has long range order of regular pattern of arrangement which repeats periodically over entire crystal.
- The interatomic or intermolecular forces are identical, hence the thermal energy required to break the regular structure by overcoming the intermolecular forces is uniform throughout.
- Hence the heat and temperature needed to melt the solid are same, and therefore solids have sharp melting points.
Q. Why Amorphous solids do not have sharp melting points. Explain.
- Amorphous solids do not have perfectly ordered crystalline structure.
- They have short range order of regular pattern hence periodically repeating regular pattern is over a short distance.
- The thermal energy required to break the structure and separate constituent particles is not uniform.
- Hence the temperature needed to melt the solid is not same, therefore amorphous solids do not have sharp melting points but melt over a range of temperature.
Distinguish between crystalline solids and amorphous solids :
| Crystalline solids | Amorphous solids |
| They have definite characteristic geometrical shape. | They have irregular shape. |
| They have long range order of regular pattern of arrangement of constituent particles. | They have short range order of regular pattern of arrangement of constituent particles. |
| They are true solids. | They are pseudo solids or supercooled liquids. |
| They have sharp melting points. | They do not have sharp melting points. |
| They are anisotropic in nature. | They are isotropic in nature.
|
| They have definite heat of fusion. | They do not have definite heat of fusion. |
Classification of crystalline solids : The solids in which the constituent particles are charged ions namely cations and anions held together by electrostatic force of attraction are called crystalline solids. Crystalline solids are further classified into four categories :
Crystalline solids are classified as follows :
- Ionic crystals.
- Covalent network crystals
- Molecular crystals.
- Metallic crystals.
Characteristics of ionic crystals :
- The constituents of ionic crystals are charged ions namely cations and anions. They differ in ionic size.
- The ions in these crystals are held by strong electrostatic force of attraction.
- Ionic crystals have high melting points and they are hard and brittle.
- In solid state they are nonconductors of electricity but they are good conductors when melted or dissolved in water.
- In aqueous solution they dissociate forming ions.
- Example : NaCl, KCI, CaF2, K2S04, etc.
In ionic crystalline solids, constituent particles are positively charged cations and negatively charged anions placed at alternate lattice points. The ions are held by strong coulombic electrostatic forces of attraction compensating opposite forces. Hence they are hard. Since there are no free electrons, they are not malleable and on applying a shearing force, ionic crystals break into small units. Hence they are brittle.
Covalent network crystals : The crystals in which the constituent particles are atoms linked by covalent bonds forming a continuous network are called covalent network crystals. For example, diamond, quartz.
In each of the four main classes of crystalline solids, the smallest constituents or particles of various solids are atoms, ions or molecules.
Characteristics of covalent network crystals :
- The constituent particles in these solids are atoms.
- The atoms in these crystals are held by covalent bonds forming a rigid three dimensional network which gives a giant molecule. Hence, the entire crystal is a single molecule.
- These crystals are very hard (or hardest) and most incompressible.
- They have high melting points and boiling points.
- Since the electrons are localised they are poor conductors of heat and electricity.
- Example : Diamond, Quartz (SiO2), Boron nitride, Carborandum.
Q. Why Graphite is a covalent solid yet soft and good conductor of electricity. Explain.
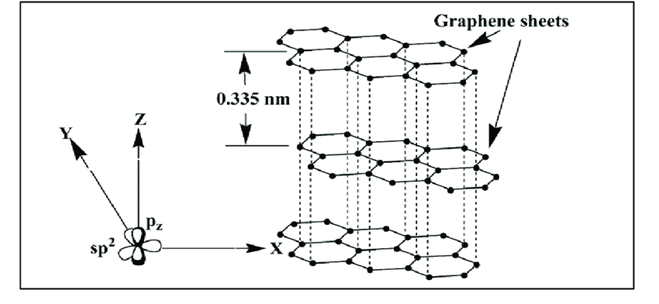
- Each carbon atom in graphite is sp2 hybridized and covalently bonded to other three sp2 hybridized carbon atoms forming s bonds and the fourth electron in 2pz orbital of each carbon atom is used in the formation of a p bond. This results in the formation of hexagonal rings in two dimensions.
- In graphite, the layers consisting of hexagonal carbon network are held together by weak van der Waal’s forces imparting softness.
- The electrons in p bonds in the ring are delocalized and free to move in the delocalised molecular orbitals giving good electrical conductance.
Remember.
|
Allotropes : When a substance exists in two or more forms then they are called allotropes. They are polymorphous. For example, carbon has allotropes diamond and graphite.
Molecular crystals : These are crystals in which the constituent particles are molecules (or unbonded single atoms) of the same substance held together by intermolecular forces of attraction. For example, solidified C12, CO2, etc.
Characteristics of molecular crystals :
- The constituent particles of these solids are molecules (or unbonded single atoms) of the same substance.
- The atoms within the molecules are bonded by covalent bonds.
- The molecules are held together by intermolecular forces of attraction.
Intermolecular forces of attraction involved in molecular crystals :
Weak dipole-dipole interactions : The solidsconstituting polar molecules like HCl, H2O, SO2, etc. which possess permanent dipole moment involve weak dipole-dipole interactions.
Very weak dispersion or London forces : The solids consisting of nonpolar molecules like CH4, H2, etc. involve weak dispersion forces. They are also involved in monoatomic solids like Ar, Ne.
Intermolecular Hydrogen bonds :
- In this crystalline solids, the constituent particles are the molecules which contain hydrogen atom linked to highly electronegative atom like F, O or N.
- In these, molecules are held by hydrogen bonds in which H atom of one molecule is bonded to electronegative atom (like F, N or O) of another molecule.
- Since hydrogen bonding is weak, these solids have very low melting points and generally. They exist in the liquid or gaseous state at room temperature.
- They are non-conductors of electricity.
Metallic crystals : These are crystalline solids formed by atoms of the same metallic element, held together by a metallic bond.
Characteristics of metallic crystals ;
- Metallic crystals are solids formed by atoms of the same metallic element held together by metallic bonds.
- Metallic crystals have high melting point and boiling point.
- Metals are malleable, that is, they can be hammered into thin sheets.
- Metals are ductile, that is, they can be drawn into wires.
- Metals have good electrical and thermal conductivity.
- Examples : metals such as Na, K, Ca, Li, Fe, Au, Ag, Co, etc.

Giant solid : Covalent solid formed by covalent bonds between neighbouring constituent atoms of non-metallic solid is called a giant solid. For example, graphite.
Crystal Structure :
Lattice : Lattice is a geometrical arrangement of points in a three dimensional periodic array.
Crystal lattice (space lattice) : A regular arrangement of the constituent particles (atoms, ions or molecules) of a crystalline solid having similar environment in three dimensional space is called crystal lattice or space lattice.
Lattice point : A position occupied by a crystal constituent particle like an atom, ion or a molecule in the crystal lattice is called lattice point or lattice site.
0R
Any point at the intersection of the lines in the unit cell occupied by a constituent particle like an atom, an ion or a molecule in the crystalline solid is called a lattice point.
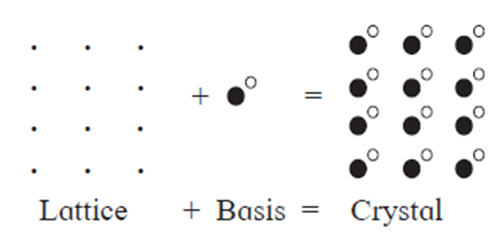
Basis of crystal lattice :
- A crystal structure is formed by attaching a constituent particle to lattice points.
- The constituent particles attached to the lattice points form the basis of the crystal lattice.
- The crystal structure is obtained by attaching a basis to each of the lattice points.
This is represented by the following schematic equation :
Unit cell : It is the smallest repeating structural unit of a crystalline solid (or crystal lattice) which when repeated in different directions produces the crystalline solid (lattice).
- The crystal is considered to consist of an infinite number of unit cells.
- The unit cell possesses all the characteristics of the crystalline solid.
Parameters of a unit cell : . A unit cell is characterised by following parameters.
Edges or edge lengths : The intersection of two faces of crystal lattice is called as edge. The three edges denoted by a, b and c represent the dimensions (lengths) of the unit cell along three axes. These edges may or may not be mutually perpendicular.

Angles between the edges (or planes) : There are three angles between the edges of the unit cell represented as α, β and γ.
- The angle α is between edges b and c.
- The angle β is between edges a and c.
- The angle γ is between edges a and b.
The crystal is defined with the help of these parameters of its unit cell.
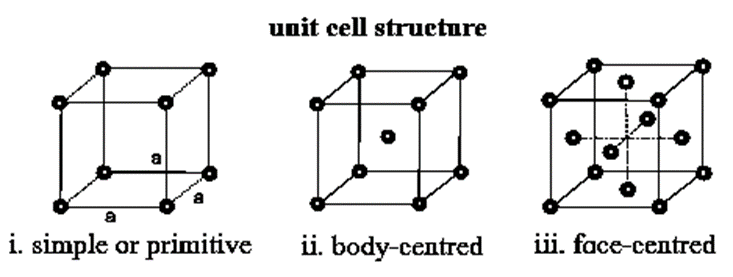
Types of unit cells : Basically unit cells are of four types as follows :
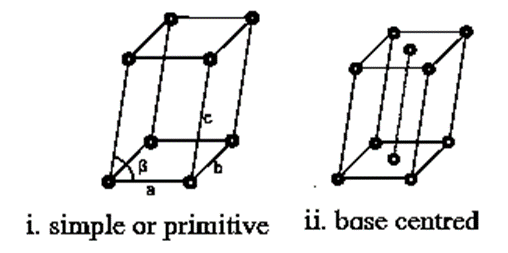
Primitive unit cell : The unit cell in which the constituent particles like atoms, ions or molecules are present only at the comers of the unit cell is called primitive unit cell or simple unit cell.
Body-centred unit cell : A unit cell in which the constituent particles are present at the comers as well as at its body-centre is called body-centred unit cell.
Face-centred unit cell : A unit cell in which the constituent particles are present at the corners as well as at the centre of each face is called face centred unit cell or cubic close packed (CCP) limit cell.
Base-centred unit cell : A unit cell in which the constituent particles are present at the corners as well as at the centres of two opposite faces is called end-centred unit cell.
Crystal systems : The constituent particles like atoms, ions or molecules of the crystal can be arranged in seven different ways changing edges (a, b, c) and angles (α, β, γ) and accordingly they form seven systems or types of the crystal.
These seven crystal system are named as :
(a) Cubic system (b) Tetragonal system (c) Orthorhombic system (d) Rhombohedral system (e) Monoclinic system (f) Triclinic system (g) Hexagonal system.
Cubic system : There are seven crystal systems according to the edges (a, b, c) and angles (α, β, γ).
- The constituents of the crystal may be present at comers, face centres, body centres, edge centres and voids.
- By mathematical analysis, it has been proved that only fourteen different kinds of space lattices are possible.
- Hence there are fourteen different ways of arrangement of the lattice basis.
- These fourteen lattices of seven crystal systems are called Bravais lattices.
Bravais lattices of a cubic system (Unit cells of a cubic system) :
Cubic lattice : For this, edges are a = b = c and angles are α = β = γ = 90°. In this cubic system, there are three Bravais lattices. Lattice points in one unit cell represent the positions of atoms, ions or molecules in the unit cell.
Simple (or primitive) cubic unit cell (SCC) : In this unit cell, atoms are present only at 8 comers of the cube.

Number of atoms in primitive simple cubic (scc) unit cell :
In simple or primitive cubic unit cell, there are 8 atoms at 8 corners. Each comer contributes 1/8th atom to the unit cell.
∴ Number of atoms present in the unit cell = (1/8) X 8 = 1
Hence the volume of the unit cell is equal to the volume of one atom.
Body-centred cubic unit cell (BCC) : In this, atoms are present at 8 comers along with one additional atom at the body-centre of the cube.
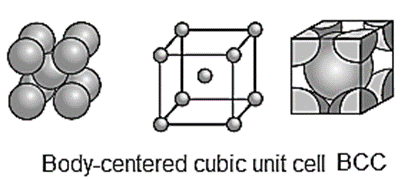
Number of atoms in body-centred cubic (bcc) unit cell :
In this unit cell, there are 8 atoms at 8 comers and one additional atom at the body centre. Each corner contributes 1/8th atom, to the unit cell, hence due to
8 comers.
∴ Number of atoms present in the unit cell = (1/8) X 8 = 1
An atom at the body centre wholly belongs to the unit cell.
Total number of atoms present in bCC cell = 1 + 1 = 2.
Hence the volume of unit cell is equal to the volume unit of two atoms.
Face-centred cubic unit cell (FCC) : In this unit cell, atoms are present at 8 corners and at 6 face centres.
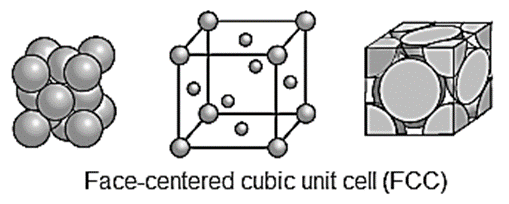
Number of atoms in face-centred cubic (fcc) unit cell :
In this unit cell, there are 8 atoms at 8 corners and 6 atoms at 6 face centres.
Each comer contributes 1/8th atom to the unit cell, hence due to 8 corners,
∴ Number of atoms present in the unit cell = (1/8) X 8 = 1
Each face centre contributes half of the atom to the unit cell, hence due to 6 face centres,
Number of atoms =1/2 x 6 = 3.
Total number of atoms present in fcc unit cell = 1 + 3 = 4.
Hence the volume of the unit cell is equal to the volume of four atoms.
The names of fourteen Bravais lattices (unit cells) for each of the seven crystal system are shown below.
1. Cubic :
2. Orthorhombic :

3. Tetragonal :
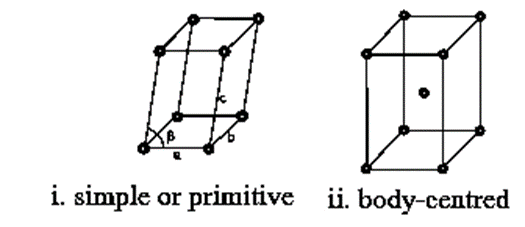
4. Monoclinic :
5. Rhombohedral :

6. Triclinic :

7. Hexagonal :

| Remember...
Each corner particle of a cube is shared by 8 cubes, each face particle is shared by 2 cubes and each edge particle is shared by 4 cubes. |
Relationship between density of a substance and the edge length of unit cell. OR Relationship between molar mass, density of the substance and unit cell edge length of the crystal :
Consider edge length of cubic unit cell is a, the
∴ Volume of unit cell = a3.
Suppose that mass of one particle is m and that there are n particles per unit cell.
∴ Mass of unit cell = m × n
The density of unit cell (ρ), which is same as density of the sub-substance is given by
Density of Unit Cell = \(\frac{\text{Mass of unit cell}}{\text{Volume of unit cell}}\)
∴ ρ = \(\frac{m×n}{a^3}\)
Relation for the density of the unit cell and radius of atom or sphere for the Simple cubic (scc) crystal :
Consider a unit cell of a simple cubic crystal. It has 8 atoms at 8 corners of the unit cell.
∴ Total number of atoms in unit cell = (1/8) X 8 = 1
If a is the length of edge of cubic unit cell and r is the radius of the atom, then
r = a/2 or a = 2r.
Volume of the unit cell = a3 = (2r)3 = 8r3
If M is atomic mass of the element, then mass of one atom is M/NA where NA is Avogadro number.
If there are ‘n’ atoms in one unit cell then,
Mass of unit cell = n x Mass of one atom = n x (M/NA)
Density of Unit Cell = \(\frac{\text{Mass of unit cell}}{\text{Volume of unit cell}}\)
∴ ρ = \(\frac{m/N_A×n}{a^3}\)
∴ ρ = \(\frac{m×n}{N_A×a^3}\)
Since there is one atom present in one unit cell,
∴ ρ = \(\frac{m}{N_A×a^3}\)
Relation for the density of the unit cell and radius of atom or sphere for the Body centred cubic (bcc) crystal :
Consider a unit cell of body centred cubic (bcc) crystal. It has 8 atoms at 8 corners and one additional atom at the centre of body of unit cell.
∴ Number of atoms due to 8 comers = (1/8) X 8 = 1
Body centred atom, wholly belong to the unit cell.
Hence total number of atoms in the unit cell is two.
If M is atomic mass of the element, then mass of one atom is M/NA where NA is Avogadro number.
Mass of unit cell = Mass of 2 atoms in unit cell = 2(M/NA)
If a is the edge length or lattice parameter then,
Volume of cubic unit cell = a3
Density of Unit Cell = \(\frac{\text{Mass of unit cell}}{\text{Volume of unit cell}}\)
∴ ρ = \(\frac{2×m/N_A}{a^3}\)
∴ ρ = \(\frac{2m}{N_A×a^3}\)
Relation for the density of the unit cell and radius of atom or sphere for the Face centred cubic (fcc) crystal :
Consider a unit cell of face centred cubic (fcc) crystal.
It has 8 atoms at 8 comers and 6 atoms at 6 face centres.
∴ Total number of atoms in unit cell = \(\frac{1}{8}×8+\frac{1}{2}×8\) = 1+3=4
If M is atomic mass of the element, then mass of one atom is M/NA where NA is Avogadro number.
Mass of unit cell = Mass of 4 atoms in unit cell = 4(M/NA)
If a is the edge length or lattice parameter then,
Volume of cubic unit cell = a3
Density of Unit Cell = \(\frac{\text{Mass of unit cell}}{\text{Volume of unit cell}}\)
∴ ρ = \(\frac{4×m/N_A}{a^3}\)
∴ ρ = \(\frac{4m}{N_A×a^3}\)
Packing of particles in crystal lattice :
Coordination number and its significance :
Coordination number : The number of the closest neighbouring constituent particles like atoms, ions or molecules which are in contact with a particular particle or an atom in the crystal lattice is called coordination number of that particle.
(In the crystal lattice, all atoms may have same or different coordination numbers.)
- The magnitude of the coordination number is a measure of compactness of spheres in close-packed structures.
- The higher the coordination number, the closer are the spheres to each other.
Linear packing in one direction or close packing in one dimension :
The constituent particles of the crystal may be of varying shapes but for better understanding we consider particles as hard spheres of equal size.
![]()
There is only one way of arranging or packing spheres placed in a horizontal row touching one another. Since one sphere is in contact with two neighbouring spheres except the end atoms, the coordination number in this arrangement is two.
This packing may be in any one direction x, y or z.
Close packing in two dimensions :
Two dimensional close packing crystal structure can be generated by placing one dimensional linear crystal structure over another to form multiple layers. This staking of linear rows may be taking place in two different ways giving two different two dimensional structures as follows :
AAAA type two dimensional close packing or square close packing :
In this arrangement, various one dimensional rows are placed on one over other so that each sphere in one row is over the another sphere of another row forming planar structure. In this, spheres have horizontal as well as vertical alignment. All the rows of spheres are identical in planar structure. All crestsas well as all the depressions or troughs formed by the arrangement are also aligned.
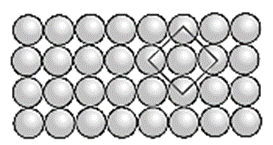
If the first row is labelled as A type, then second and all subsequent rows are also identical, hence are of A type. Therefore this planar two dimensional close packing is called AAAA…. type packing.
In this arrangement, each sphere is in contact with (or touching) four other spheres around it, hence the coordination number of each sphere is four and the packing is called two dimensional or planar square close packing. In this, packing efficiency is 52.4 %.
ABAB type two dimensional packing or hexagonal close packing :
In this arrangement, crests of the spheres of one row are placed into the depressions or troughs formed between adjacent spheres of next row. This arrangement is repeated consecutively throughout.

In this arrangement, crests of the spheres of one row are in contact with depressions or troughs of next row.
If one row of spheres is labelled as A then the next row will be B, third row will again be A, fourth row B and so on. Hence this planar or two dimensional close packing is called ABAB... type packing.
In this arrangement, each sphere is in contact with six other spheres around it hence the coordination number of each sphere is six and the packing iscalled two dimensional or planar hexagonal close packing. In this, the packing efficiency is 60.4% which is more than linear close packing.
Close packing in three dimensions : Three dimensional crystal structures are obtained by stacking of two dimensional layers. Simple cubic lattice is obtained by stacking of two dimensional square layers.
The stacking of two dimensional hexagonal close packed layers gives two structures namely hexagonal close packed (hcp) structure and face centred (fcc) structure.
(i) Stacking of square close packed layers :
In this arrangement, the two dimensional AAAA type square closed packed layers are placed one over the other in such a way that the crests of all spheres are in contact with successive layers in all directions.
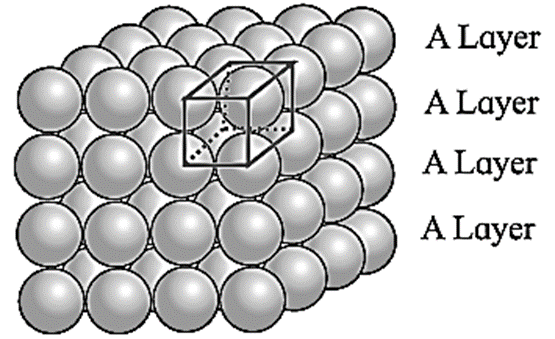
All spheres of different layers are perfectly aligned horizontally and vertically forming unit cells having primitive or simple cubic structure. Since all the layers are identical and if each layer is labelled as layer A, then whole three dimensional crystal lattice will be of type.
Each sphere is in contact with six surrounded spheres, hence the co-ordination number of each sphere is six.
(ii) Stacking of two hexagonal close packed layers :
A close packed three dimensional structure can be generated by arranging hexagonal close packed layers in a particular manner.

In this the spheres of second layer are placed in the depression of the first layer.
In this if first layer is labelled as A then second layer is labelled as B since they are aligned differently.
In this, all triangular voids of the first layers are not covered by the spheres of the second layer.
The triangular voids which are covered by second layer spheres generate tetrahedral void which is surrounded by four spheres. The triangular voids in one layer have above them triangular voids of successive layers.
The overlapping triangular voids from two layers together form an octahedral void which is surrounded by six spheres.
Placing third hexagonal close packed layer :
(i) Hexagonal close packing (hcp) : If the crests of spheres of third layer are placed on the triangular shaped tetrahedral voids C of the second layer, then three dimensional closest packing structure is obtained in which the spheres of third layer lie directly above the spheres of first layer, i.e., first and third layers are identical. Following same placing of layers, fourth layer will be identical to second layer.
If the first layer is labelled A and second layer B, then the arrangement of packing will be of ABAB type. This is also called hexagonal close packing (hcp) as shown in the figure.
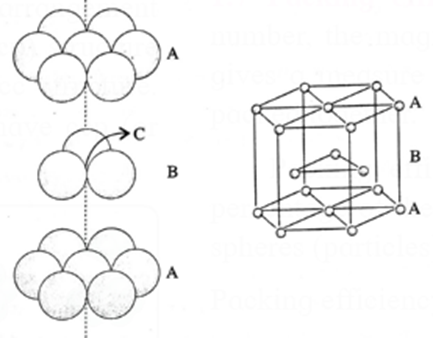
In this, packing efficiency is 74%. The coordination number of each sphere is 12. The metals Be, Mg, Zn, Cd crystallise in HCP crystalline structure.
(ii) Cubic close packing (ccp) : If the crests of spheres of third layer are placed in the positions of tetrahedral void ‘a’ having apex upward of first layers, then the third layer will not be identical to the first, and may be labelled as C, which is different from A and B layers. Fourth layer may be arranged above third layer such that the spheres are aligned, so that the first layer and fourth layer are identical, second and fifth layers are identical and so on.

If first, second and third layers are labelled as A, B and C respectively then the arrangement of packing will be ABCABC type. This is also called cubic close packing (ccp) as shown in the figure. This is similar to face centred cubic (fcc) packing.
In this, arrangement packing efficiency is 74 % and the coordination number of each sphere is 12.
Tetrahedral void: All triangular voids of the first layers are not covered by the spheres of the second layer. The triangular voids that are covered by spheres of the second layer generate tetrahedral void.
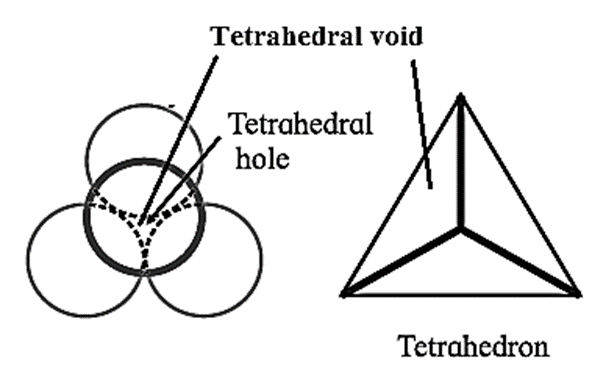
The vacant space or void among four constituent particles having tetrahedral arrangement in the crystal lattice is called tetrahedral void.
The arrangement of four spheres around the void is tetrahedral. A tetrahedral void is formed when a triangular void made by three coplanar spheres is in contact with fourth sphere above or below it.
Characteristics of tetrahedral void :
- The volume of the void is much smaller than that of atom or sphere.
- Larger the size of sphere, more is the size of void.
- If R is the radius of the constituent atom, then the radius of the tetrahedral void is 0.225 R.
- Coordination number of tetrahedral void is four.
- There are two tetrahedral voids per sphere, in the crystal lattice. If the number of closed packed spheres is N then the number of tetrahedral voids is 2N.
Octahedral void : The overlapping triangular voids from the two layers together form an octahedral void which is surrounded by six spheres.
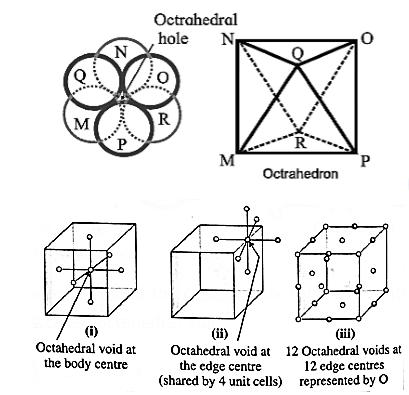
The vacant space or void at the centre of six spheres (or atoms) which are placed octahedrally is called octahedral void.
Characteristics of octahedral void :
- The volume of the void is small.
- There is one octahedral void at the body centre and twelve octahedral void positions at twelve edge centres.
- If R is the radius of constituent atom, then the radius of the octahedral void is 0.414 R.
- The coordination number of octahedral void is six.
- There is one octahedral void per sphere in the crystal lattice. If the number of closed packed spheres is N then the number of octahedral voids is N.
Number of voids per atom in hcp and ccp : The tetrahedral and octahedral voids occur in hcp and ccp/fcc structures. There are two tetrahedral voids associated with each atom. The number of octahedral voids is half that of tetrahedral voids. Thus, there is one octahedral void per atom.
- If N denotes number of particles, then number of tetrahedral voids is 2N and that of octahedral voids is N.
| Remember :
It is important to note that the triangular shapes of depressions in A and B layer do not overlap. The apices of two triangular depressions in A and B layer point in opposite directions. The depressions in which spheres of second layer rest are tetrahedral voids while the depressions in which no sphere rests are octahedral voids. |
PDF : Class-12-Chemistry-Chapter-1-Solid State-Text Book
PDF : Class-12-Chemistry-Chapter-1-Solid State- Notes
PDF : Class-12-Chemistry-Chapter-1-Solid State- Solution
All 16 Chapters Notes -Class-12-Chemistry (16-PDF)
All 16 Chapters Solutions -Class-12-Chemistry (16-PDF)
All 16 Chapters Notes+Solutions -Class-12-Chemistry (32-PDF)
Main Page : – Maharashtra Board Class 12th-Chemistry – All chapters notes, solutions, videos, test, pdf.
Next Chapter : Chapter-2-Solutions – Online Notes

Hello sir your notes are so amazing and helpful to us. It helps to clear all the doubts in chemistry.
It’s a request to upload all 12th state board chemistry and physics notes on the site.
Your faithful
…