Solutions-Class-11-Science-Physics-Chapter-10-Electrostatics-Maharashtra Board

(C) same as that on the glass rod but lesser in quantity

(A) be attracted to the +ve plate

(C) 1:1

(B) 9 × 10⁹ N

(B) double the previous distance

(B) 2:1

(C) two parallel plates

(C) a direction parallel to line AB

The magnitude of charge on an electron = 1.602 × 10⁻¹⁹C.

In any closed or isolated system, the algebraic sum of all the electric charges is constant, i.e., the net charge cannot be created or destroyed.

• The SI unit of charge is the coulomb (C).
• Using Coulomb's law, it is defined as follows : One coulomb is the amount of charge, which placed at a distance of one metre from another charge of the same magnitude in vacuum, experiences a force of 9.0 x 10⁹

Given : V = 10 V, d = 0.5 mm = 5 x 10⁻⁴ m

The strength of the electric field,

E = \(\frac{V}{d}\) = \(\frac{10}{5×10^{-4}}\)  = 2 x 10⁴ V/m = 2 x 10⁴ N/C

A uniform electric field is an electric field that has the same magnitude and the same direction at all points in a given region.

If two lines of force intersect at a point, it would mean electric field has two directions at that point. This is impossible.

SI unit of linear charge density λ is (C/m).

The SI unit of electric dipole moment is the coulomb-metre (C.m). The debye (D) is a non SI unit of electric dipole moment.

1 debye = 3.33564 x 10^—30 coulomb-metre.

The relative permittivity (ε_r) ( ≡ dielectric constant) of a medium is the ratio of the absolute permittivity of the medium (ε) to the absolute permittivity of free space (≡ vacuum (ε₀)).

Relative permittivity ε_r = \(\frac{ε}{ε_0}\)

Given : r = 18 cm = 18 x 10⁻²m, F = 6 x 10⁻⁸ , \(\frac{1}{4πε_0}\) = 9 x 10⁹ Nm²/C²,

q₁ = q₂ = q(Say)

F = \(\frac{1}{4πε_0}(\frac{q_1q_2}{r^2})\) = \(\frac{1}{4πε_0}(\frac{q^2}{r^2})\)

∴ q² = F (4πε₀) r² = \(\frac{(6×10^{-8})(18×10^{-2})}{9×10^9}\)

= 6 x 2 x 18 x 10⁻²¹ = 21.6 x 10⁻²⁰

∴ q = \(\sqrt{21.6}\) x 10⁻¹⁰ = −4.648 x 10⁻¹⁰   ….(as the charge is negative)

∴ 2q = −9.296 x 10⁻¹⁰ C

This gives the total charge on both spheres.

Given : F = — 0.2 N, r = 25.0 cm = 0.25 m, q₁ = +q, q₂ = −2q, \(\frac{1}{4πε_0}\) = 9 x 10⁹ N.m²/C²,

F = \(\frac{1}{4πε_0}(\frac{q_1q_2}{r^2})\) = \(\frac{1}{4πε_0}(\frac{-2q^2}{r^2})\)

∴ -2q² = F (4πε₀) r² = \(\frac{(-0.2)×(0.25)^2}{9×10^9}\)

∴ q² = \(\frac{(0.1)×(0.625)}{9×10^9}=\frac{62.5}{9}\) x 10⁻¹²

∴ q = \(\frac{\sqrt{62.5}}{3}\) x 10⁻⁶

= 2.635 x 10⁻⁶ C = 2.635 μC

Given : q₁ = q₂ = q₃ = q₄ = q = +6 × 10⁻⁸ C, a = 3 cm = 3 x 10⁻² m, \(\frac{1}{4πε_0}\) = 9 x 10⁹ N.m²/C²

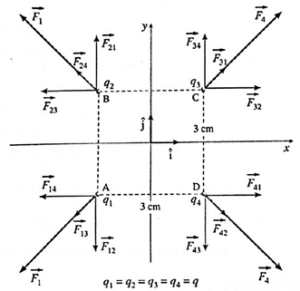
Each charge is repelled by the other three. The charges being equal, the magnitudes, F₁₄, F₁₂ , F₂₁ , F₂₃, F₃₂, F₃₄, F₄₁ and F₄₃ are all equal to

\(\frac{1}{4πε_0}(\frac{q^2}{a^2})\) = \(\frac{(9×10^9)(6×10^{-8})^2}{(3×10^{-2})^2}\) = 36 mN

With \(\vec{F}_{14}=-\vec{F}_{41}\), \(\vec{F}_{12}=-\vec{F}_{21}\), \(\vec{F}_{23}=-\vec{F}_{32}\), and \(\vec{F}_{34}=-\vec{F}_{43}\),

Also, F₁₃, F₃₁, F₂₄ and F₄₂ are equal to

\(\frac{1}{4πε_0}(\frac{q^2}{2a^2})\) = \(\frac{(9×10^9)(6×10^{-8})^2}{2(3×10^{-2})^2}\) = 18 mN

With the choice of axes as shown in Fig. the unit vectors along \(\vec{CA}\), \(\vec{AC}\), \(\vec{DB}\), and \(\vec{BD}\)

are respectively, \(\frac{-\hat{i}-\hat{j}}{\sqrt{2}}\), \(\frac{\hat{i}+\hat{j}}{\sqrt{2}}\), \(\frac{-\hat{i}+\hat{j}}{\sqrt{2}}\) and \(\frac{\hat{i}-\hat{j}}{\sqrt{2}}\)

The net force on q₁ is

\(\vec{F}_1=\vec{F}_{12}+\vec{F}_{14}+\vec{F}_{13}\)

= (36)(\(-\hat{j}\)) + (36)(\(-\hat{i}\) ) + (18)\((\frac{-\hat{i}-\hat{j}}{\sqrt{2}})\)

= (36 + 9\((\sqrt{2}\))\((-\hat{i}-\hat{j})\) = (48.73 mN)\((-\hat{i}-\hat{j})\)

∴ The net force on q₃ is

\(\vec{F}_3=-\vec{F}_1\) = (48.73 mN)\((\hat{i}+\hat{j})\)

The net force on q₂ is

\(\vec{F}_2\) = (48.73 mN)\((-\hat{i}+\hat{j})\)

and the net force on q₄ is

\(\vec{F}_4=-\vec{F}_2\) = (48.73 mN)\((\hat{i}-\hat{j})\)

F₁ = F₂ = F₃ = F₄ = 48.73\(\sqrt{2}\)  mN = 68.92 mN

Given : \(\vec{E}\) = 5.0\(\hat{k}\)  V/m, a = 10.0 cm = 0.1 m

Flux, ø = \(\vec{E}.\vec{dS}\)

(i) The square is along the xy-plane. The corresponding area vector,

\(\vec{dS}\) = a²\(\hat{k}\) = 0.01 \(\hat{k}\) m²

∴ The electric flux through the square

= \(\vec{E}\)·(0.01 \(\hat{k}\)) = (5 \(\hat{k}\) V/m)·(10^-2 \(\hat{k}\) m²)

= 5 x 10^-2 V.m    ….(as \(\hat{k}\).\(\hat{k}\) = 1)

(ii) The square is along the xz-plane.

The corresponding area vector,

\(\vec{dS}\) = a² \(\hat{j}\) = (10^-2 m²)\(\hat{j}\)

∴ The electric flux = (5 \(\hat{k}\) V/m)·(10^-2 \(\hat{j}\) m²) = 0   …. (as \(\hat{k}\).\(\hat{j}\) = 0)

Alternatively, the square is parallel to  so that electric field lines do not pass through the square. Hence, the electric flux through the square is zero.

(iii) The normal to the square makes an angle θ = 45° with the z-axis.

cos θ = cos 45⁰ = \(\frac{1}{\sqrt{2}}\)

.'. The electric flux through the square

= E S cos θ

= (5 V/m) (10^-2 m²) x \(\frac{1}{\sqrt{2}}\)

= 5 × 10^-2 × 0.7071

= 3.5355 × 10^-2 V/m

Given: q_A = q_B = q_C = 10 x 10⁻⁸ C

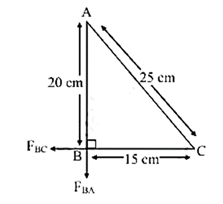
Force on B due to A,

\(\vec{F}_{BA}\) = \(\frac{1}{4πε_0}(\frac{q_A.q_B}{r^2_{AB}})\) = \(\frac{(9×10^9)(10×10^{-8})^2}{(20×10^{-2})^2}\)

= 2.25 x 10^-3 N

Force on B due to C,

\(\vec{F}_{BC}\) = \(\frac{1}{4πε_0}(\frac{q_C.q_B}{r^2_{CB}})\) = \(\frac{(9×10^9)(10×10^{-8})^2}{(15×10^{-2})^2}\)

= 4 x 10^-3 N

∴ Resultant force on point B,

|FB| = \(\sqrt{F_{BA}^2+F_{Bc}^2+2F_{BA}.F_{BC}\,cos\,90^0}\)

 = \(\sqrt{(2.25×10^{-3})^2+(4×10^{-3} )^2}\)

= 4.589 x 10⁻³ N

Force exerted on charge at point B is 4.589 x 10⁻³ N

Given: V = 5000 volt, d = 5 cm = 5 x 10⁻² m, q = 9.6 x 10⁻⁹ c, a. Electric field intensity (E) = ? Force (F) = ?

(a) Electric field intensity between the plates E = \(\frac{V}{d}=\frac{5000}{5×10^{-2}}\) = 1 x 10⁵ N/C

(b) The force on the oil drop F = qE = (9.6 x 10⁻⁹) x (1 x 10⁵) = 9.6 x 10⁻¹⁴ N

Given : q = —8 x 10⁻⁸ C, r = 5.0 cm = 5 x 10⁻² m, \(\frac{1}{4πε_0}\) = 9 x 10⁹ N.m²/C²,

The magnitude of electric field

E = \(\frac{1}{4πε_0}.\frac{q^2}{r^2}\) = \((9×10^9).\frac{(-8×10^{-8})^2}{(5×10^{-2})^2}\) = \(-\frac{72}{25}\) x 10⁵ = −2.88 x 10⁵