Mensuration
Class-10-Mathematics-2-Chapter-7-Maharashtra Board
Solutions
Practice set 7.1
Question 1.1. Find the volume of a cone if the radius of its base is 1.5 cm and its perpendicular height is 5 cm.
The radius (r) of the cone = 1.5 cm, Its perpendicular height (h) = 5 cm
Volume of the cone = \(\frac{1}{3}\)πr2h = \(\frac{1}{3}×\frac{22}{7}\) × 1.5 × 1.5 × 5 = \(\frac{82.5}{7}\) = 11.785 ≈ 11.79 cm3
Answer is : Volume of the cone is 11.79 cm3.
Question 1.2. Find the volume of a sphere of diameter 6 cm.
Diameter of a sphere = 6 cm, its radius(r) = 3 cm
Volume of the sphere = \(\frac{4}{3}\)πr3 = \(\frac{4}{3}\) × 3.14 × 3 × 3 × 3 = 113.04 cm3
Answer is : Volume of the sphere is 113.04 cm3.
Question 1.3. Find the total surface area of a cylinder if the radius of its base is 5 cm and height is 40 cm.
The radius (r) of the base of the cylinder = 5 cm, its height (h) = 40 cm
Total surface area of the cylinder = 2πr(r + h)
= 2 × 3.14 × 5(5 + 40)
= 3.14 ×10 × 45
= 1413 cm2
Answer is : Total surface area of the cylinder is 1413 cm2.
Question 1.4. Find the surface area of a sphere of radius 7 cm.
The radius of the sphere (r) = 7 cm.
Surface area of the sphere = 4πr2 = 4 × \(\frac{22}{7}\) × 7 × 7 = 88 × 7 = 616 cm2
Answer is : Surface area of the sphere is 616 cm2.
Question 1.5. The dimensions of a cuboid are 44 cm, 21 cm, 12 cm. It is melted and a cone of height 24 cm is made. Find the radius of its base.
The length (l) of a cuboid = 44 cm, its breadth (b) = 21 cm, its height (h) = 12 cm
The height of the cone (h1) = 24 cm
Let the radius of the base of the cone be r.
Cuboid is melted and a cone is made.
∴ volume of cuboid = volume of cone
∴ l x b x h = \(\frac{1}{3}\) x πr2h1
∴ 44 x 21 x 12 = \(\frac{1}{3}×\frac{22}{7}\) x r2 x 24
∴ r2 = \(\frac{44×21×12×3×7}{22×24}\) = 21 x 21
∴ r = 21 cm ... (Taking square roots of both the sides)
Answer is : The radius of the base of the cone is 21 cm.
Question 1.6. Observe the measures of pots in figure 7.8 and 7.9. How many jugs of water can the cylindrical pot hold ?
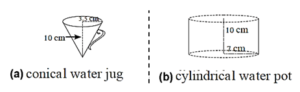
The radius (r) of the conical water jug = 3.5 cm, its height (h) = 10 cm,
The radius (r1) of the cylindrical water pot = 7 cm, its height (h1) = 10 cm.
Number of jugs of water that cylindrical pot can hold = \(\frac{\text{Volume of cylindrical water pot}}{\text{Volume of cylindrical water jug}}\)
\(\frac{πr_1^2h_1}{\frac{1}{3}×πr^2h}\) = \(\frac{7×7×10}{\frac{1}{3}×3.5×3.5×10}\) = 2 × 2 × 3 = 12
Answer is : The cylindrical pot can hold 12 jugs of water.
Question 1.7. A cylinder and a cone have equal bases. The height of the cylinder is 3 cm and the area of its base is 100 cm2.The cone is placed upon the cylinder. Volume of the solid figure so formed is 500 cm3. Find the total height of the figure.
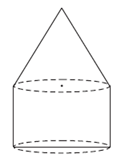
A cylinder and a cone have equal bases. ∴ they have equal radii.
Let the radius be r.
Area of its base = 100 cm2
∴ πr2 = 100 cm2 ….(1)
Let the height of the cylinder be h1 and that of the cone be h2.
h1 = 3 cm
Volume of the solid figure = 500 cm3
∴ volume of the cylindrical part + volume of conical part = 500
∴ πr2h1 + \(\frac{1}{3}\)πr2h2 = 500
∴ 100 × 3 + \(\frac{1}{3}\) × 100 × h2 = 500 ….[From (1)]
∴ 300 + \(\frac{100}{3}\)h2 = 500
∴ \(\frac{100}{3}\)h2 = 500 – 300 = 200
∴ h2 = \(\frac{200×3}{100}\) = 6
∴ h2 = 6 cm
Height of the figure = h1 + h2 = 3 + 6 = 9 cm.
Answer is : The total height of the figure is 9 cm.
[Note : The answer in the textbook is given as 5 cm, whereas the correct answer is 9 cm.]
Question 1.8. In figure, a toy made from a hemisphere, a cylinder and a cone is shown. Find the total area of the toy.

A toy is made up of hemisphere, cylinder and a cone.
They have equal bases.
Let their radius be r.
∴ r = 3 cm.
Let the heights of the conical part and cylindrical part be h1 and h2 respectively.
h1 = 4 cm and h2 = 40 cm.
Let the slant height of the cone be l.
l 2 = r2 + h12
∴ l 2 = 32 + 42
∴ l 2 = 9 + 16
∴ l 2 = 25
∴ l = 5 cm ... (Taking square roots of both the sides)
Total area of the toy = curved surface area of the cone + curved surface area of the cylinder + curved surface area of the hemisphere
= πrl + 2πrh2 + 2πr2
= πr(l + 2h2 + 2r)
= π × 3(5 + 2×40 + 2×3)
= π × 3(5 + 80 + 6)
= π × 3 (91)
= 273π cm2
Answer is : Total area of the toy is 273π cm2
Question 1.9. In the figure, a cylindrical wrapper of flat tablets is shown. The radius of a tablet is 7 mm and its thickness is 5 mm. How many such tablets are wrapped in the wrapper ?

The radius (r) of the tablet = 7 mm, its thickness (h) = 5mm
The diameter of the wrapper = 14 mm, ∴ its radius (r1) = 14/2 = 7 mm
its length (h1) = 10 cm = 100 mm
Number of tablets that can be wrapped in the wrapper = \(\frac{\text{Volume of the wrapper}}{\text{Volume of each tablet}}\)
= \(\frac{πr_1^2h_1}{πr^2h}\) = \(\frac{7×7×100}{7×7×5}\) = 20
Answer is : 20 tablets can be wrapped in the wrapper.
Question 1.10. Figure shows a toy. Its lower part is a hemisphere and the upper part is a cone. Find the volume and the surface area of the toy from the measures shown in the figure.( π = 3.14)
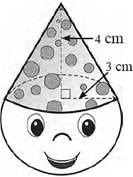
A toy is made up of a cone and a hemisphere.
They have equal bases.
Let the radius of the base be r.
∴ r = 3 cm
Height of the conical part (h) = 4 cm
Let the slant height of the cone be l
l2 = r2 + h2
∴ l2 = 32 + 42
∴ l2 = 9 + 16
∴ l2 = 25
∴ l = 5 ... (Taking square roots of both the sides)
Surface area of the toy = Curved surface area of the conical part + Curved surface area of the hemispherical part
= πrl + 2πr2
= πr (l + 2r)
= 3.14 × 3(5 + 2 × 3)
= 3.14 × 3 × 11
= 3.14 × 33 = 103.62 cm2
Volume of the toy = Volume of conical part + Volume of hemispherical part
= \(\frac{1}{3}\)πr2h + \(\frac{2}{3}\)πr3 = \(\frac{1}{3}\)πr2(h + 2r) = \(\frac{1}{3}\) × 3.14 × 9(4 + 2 × 3) = 94.2 cm3
Answer is : The surface area of the toy is 103.62 cm2 and the volume of the toy is 94.2 cm3.
Question 1.11. Find the surface area and the volume of a beach ball shown in the figure.
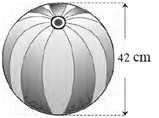
The diameter of the beach ball = 42 cm, ∴ its radius (r) = 42/2 = 21 cm
Surface area of the beach ball = 4πr2 = 4 × 3.14 × 21 × 21 = 5538.96 cm2
Volume of the beach ball = \(\frac{4}{3}\)πr3 = \(\frac{4}{3}\) × 3.14 × (21)3 = 38772.72 cm3
Answer is : Surface area of the beach ball is 5538.96 cm2 and volume of the beach ball is 38772.72 cm3.
Question 1.12. As showm in the figure, a cylindrical glass contains water. A metal sphere of diameter 2 cm is immersed in it. Find the volume of the water.
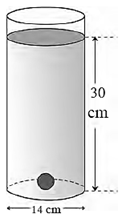
Diameter of the cylindrical glass = 14 cm, ∴ r = 7 cm
Volume of the water with metallic sphere immersed in it = πr2h = π × 49 × 30
= 1470π cm3 …..(1)
Diameter of the metallic sphere = 2 cm. ∴ r1 = 1 cm
Volume of the metallic sphere = \(\frac{4}{3}\)πr13 = \(\frac{4}{3}\) × π × 13 = \(\frac{4}{3}\)π = 1.33 π cm3 …..(2)
To find the volume of water in the cylinder, subtract the result (2) from the result (1).
∴ Volume of water = (1470 π − 1.33 π) cm3 = 1468.67 π cm3
Answer is : Volume of water is 1468.67 π cm3.
Practice set 7.2
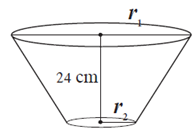
Question 2.1. The radii of two circular ends of frustum shape bucket are 14 cm and 7 cm. Height of the bucket is 30 cm. How many liters of water it can hold ? (1 litre = 1000 cm3)
The radii of two circular ends of frustum shape bucket are 14 cm and 7 cm.
∴ r1 = 14 cm and r2 = 7 cm, its height (h) = 30 cm
Volume of the bucket = \(\frac{1}{3}\)π (r12 + r22 + r1 x r2) x h
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × (142 + 72 + 14 × 7) × 30
= \(\frac{22}{7}\) × 343 × 10
= 10780 cm3 = litres ……(∵ 1 litre = 1000 cm3)
= 10.78 litres.
Answer is : Bucket can hold 10.78 litres of water.
Question 2.2. The radii of ends of a frustum are 14 cm and 6 cm respectively and its height is 6 cm. Find its (i) curved surface area (ii) total surface area. (iii) volume (π = 3.14)
The radii of ends of a frustum are 14 cm and 6 cm.
∴ r1 = 14 cm and r2 = 6 cm
its height (h) = 6 cm
Let the slant height of the frustum be l.
l = \(\sqrt{h^2+(r_1-r_2)^2}\)
∴ l = \(\sqrt{6^2+(14-6)^2}\)
∴ l = \(\sqrt{100}\) = 10 cm
Curved surface area of a frustum = πl(r1 + r2)
= 3.14 × 10 × (14 + 6) = 3.14 × 10 × 20 = 628 cm2
Total surface area of a frustum = πl(r1 + r2) + πr12 + πr22
= 628 + π(r12 + r22)
= 628 + 3.14 (142 + 62)
= 628 + 3.14(196 + 36)
= 628 +3.14 × 232
= 628 + 728.48
= 1356.48 cm2
Volume of the frustum = \(\frac{1}{3}\)πh(r12 + r22 + r1 x r2)
= \(\frac{1}{3}\) x 3.14 × 6 ×(142 + 62 + 14 × 6)
= 3.14 × 2 × (196 + 36 + 84)
= 6.28 × 316
= 1984.48 cm3
Answer is : Curved surface area of a frustum is 628 cm2, Total surface area of a frustum is 1356.48 cm2 and Volume of frustum is 1984.48 cm3.
Question 2.3. The circumferences of circular faces of a frustum are 132 cm and 88 cm and its height is 24 cm. To find the curved surface area of the frustum complete the following activity. (π = 22/7 ).
circumference1 = 2πr1 = 132
r1 = \(\frac{132}{2π}\) = […..]
circumference2 = 2πr2 = 88
r2 = \(\frac{88}{2π}\) = […..]
slant height of frustum, l = \(\sqrt{h^2+(r_1-r_2)^2}\) = \(\sqrt{[...]^2+([...])^2}\) = […..] cm
curved surface area of the frustum = π(r1 + r2)l
= π × [….] × [….]
= […..] sq.cm.
circumference1 = 2πr1 = 132
r1 = \(\frac{132}{2π}\) = [21 cm]
circumference2 = 2πr2 = 88
r2 = \(\frac{88}{2π}\) = [14 cm]
slant height of frustum, l = \(\sqrt{h^2+(r_1-r_2)^2}\) = \(\sqrt{[24]^2+([7])^2}\) = [25] cm
curved surface area of the frustum = π(r1 + r2)l
= π × [35] × [25]
= [2750] sq.cm.
Practice set 7.3
Question 3.1. Radius of a circle is 10 cm. Measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (π = 3.14 )
The radius (r) of a circle =10 cm,
Measure of an arc of the circle (θ) = 54°
Area of the sector = \(\frac{θ}{360}\) × πr2 = \(\frac{54}{360}\) × 3.14 × 102 = 3 × 1.57 × 10 = 47.10 cm2
Answer is : Area of the sector associated with the given arc is 47.10 cm2.
Question 3.2. Measure of an arc of a circle is 80° and its radius is 18 cm. Find the length of the arc. (π = 3.14 )
Measure of an arc of a circle (θ) = 80°, its radius (r) = 18 cm.
Length of the arc = \(\frac{θ}{360}\) × 2πr = \(\frac{80}{360}\) × 2 × 3.14 × 18 = 3.14 × 8 = 25.12 cm
Answer is : Length of the arc is 25.12 cm.
Question 3.3. Radius of a sector of a circle is 3.5 cm and length of its arc is 2.2 cm. Find the area of the sector.
The radius (r) of the sector of a circle = 3.5 cm.
Length of the arc = 2.2 cm.
Area of a sector = \(\frac{\text{length of the arc × radius}}{2}\) = \(\frac{2.2×3.5}{2}\) = 3.85 cm2
Answer is : Area of the sector is 3.85 cm2.
Question 3.4. Radius of a circle is 10 cm. Area of a sector of the sector is 100 cm2. Find the area of its corresponding major sector. (π = 3.14)
The radius (r) of a circle =10 cm.
Area of the circle = πr2 = 3.14 × 10 × 10 = 314 cm2
Area of the sector = 100 cm2 ... (Given)
Area of corresponding major sector = Area of the circle − Area of the minor sector
= 314 – 100 = 214 cm2
Answer is : Area of the corresponding major sector is 214 cm2.
Question 3.5. Area of a sector of a circle of radius 15 cm is 30 cm2. Find the length of the arc of the sector.
The radius (r) of the circle = 15 cm.
Area of the sector = 30 cm2.
Area of the sector = \(\frac{\text{length of the arc × radius}}{2}\)
30 = \(\frac{\text{length of the arc × 15}}{2}\)
∴ length of the arc = \(\frac{30×2}{15}\) = 4
∴ length of the arc = 4 cm
Answer is : Length of the arc is 4 cm.
Question 3.6. In the figure, radius of the circle is 7 cm and m(arc MBN) = 60°, find
(1) Area of the circle,
(2) A(O − MBN),
(3) A(O − MCN).
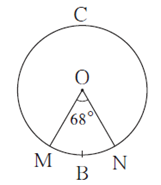
The radius (r) of the circle = 7 cm, m(arc MBN) = θ = 60°
(1) Area of the circle = πr2 = \(\frac{22}{7}\) × 7 × 7 = 154 cm2 ….(1)
(2) A(O−MBN) = \(\frac{θ}{360}\) × πr2 = \(\frac{60}{360}\) × 154 …[from (1)]
= \(\frac{154}{6}\) = 25.7 cm2
(3) A(O−MCN) = Area of the circle − A(O−MBN)
= 154 − 25.7 = 128.3 cm2
Answer is : (1) Area of the circle = 154 cm2, (2) A(O−MBN) = 25.7 cm2 and (3) A(O−MCN) = 128.3 cm2.
Question 3.7. In figure, radius of circle is 3.4 cm and perimeter of sector P−ABC is 12.8 cm. Find A(P−ABC).
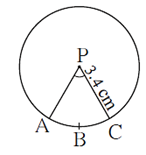
The radius (r) of the circle = 3.4 cm.
Perimeter of sector P−ABC = 12.8 cm.
Perimeter of sector P−ABC = r + r + length of arc ABC
∴ 12.8 =3.4 +3.4 + length of arc ABC
∴ 12.8 = 6.8 + length of arc ABC
∴ length of arc ABC = 12.8 − 6.8
∴ length of arc ABC = 6 cm
A(P−ABC) = \(\frac{\text{length of the arc × radius}}{2}\) = \(\frac{6×3.4}{2}\) = 10.2 cm2
Answer is : A(P−ABC) = 10.2 cm2.
Question 3.8. In figure O is the centre of the sector. ∠ ROQ = ∠ MON = 60°. OR = 7 cm, and OM = 21 cm. Find the lengths of arc RXQ and arc MYN. (π = 22/7)
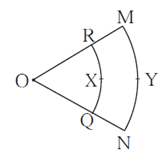
For arc RXQ,
radius(r) = OR = 7 cm
m(arc RXQ) = ∠ ROQ = θ = 60°
For arc MYN,
radius (r1) = OM = 21 cm
m(arc MYN) = ∠ MON = θ = 60°
Length of arc RXQ = \(\frac{θ}{360}\) × 2πr = \(\frac{60}{360}\) × 2 × \(\frac{22}{7}\) × 7 = \(\frac{44}{6}\) = 7.3 cm
Length of arc MYN = \(\frac{θ}{360}\) × 2πr1 = \(\frac{60}{360}\) × 2 × \(\frac{22}{7}\) × 21 = 22 cm
Answer is : Length of arc RXQ is 7.3 cm and length of arc MYN is 22 cm.
Question 3.9. In figure, if A(P−ABC) = 154 cm2 radius of the circle is 14 cm, find (1) ∠ APC. (2) l(arc ABC) .
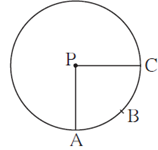
The radius (r) of the circle = 14 cm.
A(P−ABC) = 154 cm2.
Let m(arc ABC) = APC = θ
A(P−ABC) = \(\frac{θ}{360}\) × πr2
∴ 154 = \(\frac{θ}{360}\) × \(\frac{22}{7}\) × (14)2
∴ θ = \(\frac{154×360×7}{22×14×14}\) = 90° ∴ ∠ APC = 90°
Area of the sector = \(\frac{\text{length of the arc × radius}}{2}\)
∴ A(P−ABC) = \(\frac{\text{l(arc ABC) × r}}{2}\)
∴ 154 = \(\frac{\text{l(arc ABC) × 14}}{2}\)
∴ l(arc ABC) = \(\frac{154}{7}\) = 22 cm
Answer is : ∠ APC = 90° and l(arc ABC) = 22 cm.
Question 3.10. Radius of a sector of a circle is 7 cm. If measure of arc of the sector is − (1) 30° (2) 210° (3) three right angles; find the area of the sector in each case.
(i) The radius (r) of a sector of a circle =7 cm.
Measure of an arc of the sector (θ) = 30°
Area of the sector = \(\frac{θ}{360}\) × πr2 = \(\frac{30}{360}\) × \(\frac{22}{7}\) × (7)2 = 12.83 cm2
(ii) The radius (r) of a sector of a circle = 7 cm.
Measure of an arc of the sector (θ) = 210°
Area of the sector = \(\frac{θ}{360}\) × πr2 = \(\frac{210}{360}\) × \(\frac{22}{7}\) × (7)2 = = 89.83 cm2
(iii) The radius (r) of a sector of a circle = 7 cm.
Measure of an arc of the sector (θ) = 3 right angles = 3 × 90° = 270°
Area of the sector = \(\frac{θ}{360}\) × πr2 = \(\frac{270}{360}\) × \(\frac{22}{7}\) × (7)2 = \(\frac{3×22×7}{4}\) = 115.5 cm2
Answer is :
(1) Area of the sector is 12.83 cm2, when measure of the arc is 30°.
(2) Area of the sector is 89.83 cm2, when measure of the arc is 210°.
(3) Area of the sector is 115.5 cm2, when measure of the arc is equal to three right angles.
Question 3.11. The area of a minor sector of a circle is 3.85 cm2 and the measure of its central angle is 36°. Find the radius of the circle.
Area of a minor sector of a circle is 3.85 cm2
Measure of its central angle (θ) = 36°.
Let its radius be r.
Area of the sector = \(\frac{θ}{360}\) × πr2
∴ 3.85 = \(\frac{36}{360}\) × \(\frac{22}{7}\) × r2
∴ r2 = \(\frac{38.5×7}{22}\) = 12.25
∴ r = 3.5 cm
Answer is : The radius of the circle is 3.5 cm.
Question 3.12. In figure, □ PQRS is a rectangle. If PQ = 14 cm, QR = 21 cm, find the areas of the parts x, y and z .
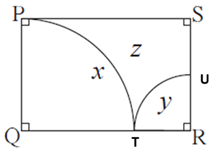
□ PQRS is a rectangle.
PQ = 14 cm and QR = 21 cm ... (Given)
Consider points M and N as shown.
Parts x and y are sectors.
For part x,
radius (r) = PQ = 14 cm
m(arc PT) = ∠ PQT = θ = 90°
Area of part x = \(\frac{θ}{360}\) × πr2 = \(\frac{90}{360}\) × \(\frac{22}{7}\) × 142 = 154 cm2
QT = PQ = 14 cm ... (Radii of the same arc)
QT + TR = QR ... (Q−T−R)
∴ 14 + TR = 21
∴ TR = 21 − 14
∴ TR = 7 cm
For part y,
radius (r1) = TR = 7 cm
m(arc TU) = ∠ TRU = θ1 = 90°
Area of part y = \(\frac{θ_1}{360}\) × πr12 = \(\frac{90}{360}\) × \(\frac{22}{7}\) × 72 = 38.5 cm2
Area of rectangle = length x breadth
A(□ PQRS) = QR x PQ
∴ A(□ PQRS) = 21 x 14
∴ A(□ PQRS) = 294 cm2
Area of part z,
= A(□ PQRS) − Area of part x − Area of part y
= 294 – 154 − 38.5
= 101.5 cm2
Answer is : Area of part x is 154 cm2, area of part y is 38.5 cm2 and area of part z is 101.5 cm2.
Question 3.13. Δ LMN is an equilateral triangle. LM = 14 cm. As shown in figure, three sectors are drawn with vertices as centres and radius 7 cm. Find,
(1) A (Δ LMN)
(2) Area of any one of the sectors.
(3) Total area of all the three sectors.
(4) Area of the shaded region.
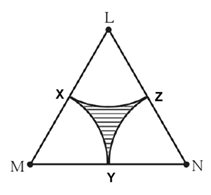
Δ LMN is equilateral.
Consider points X, Y and Z as shown.
(1) Side of equilateral triangle = LM = 14 cm.
Area of an equilateral triangle = \(\frac{\sqrt{3}}{4}\) x side2
∴ A(Δ LMN)= \(\frac{\sqrt{3}}{4}\) x 142 = \(\frac{\sqrt{3}}{4}\) x 196
∴ A(Δ LMN) = 1.732 × 49 …(as \(\sqrt{3}\) = 1.732)
∴ A(Δ LMN) = 84.868
∴ A(Δ LMN) ~ 84.87 cm2
(2) For a sector L−XZ,
radius (r) = 7 cm
Angular measure of arc (θ) = m(arc XZ) = ∠ XLZ = 60° ……(Angle of equilateral triangle)
Area of the sector L−XZ = \(\frac{θ}{360}\) × πr2 = \(\frac{60}{360}\) × \(\frac{22}{7}\) × 72 = 25.67 cm2
(3) Total area of 3 sectors =3 x Area of the sector L−XZ = 3 × 25.67 = 77.01 cm2
(4) Area of the shaded portion = A(Δ LMN) − Total area of 3 sectors
= 84.87 − 77.01 = 7.86 cm2
Answer is : (1) A(Δ LMN) = 84.87 cm2,
(2) Area of one of the sectors is 25.67 cm2,
(3) Total area of 3 sectors is 77.01 cm2,
(4) Area of the shaded portion is 7.86 cm2.
Practice set 7.4
Question 4.1. In figure, A is the centre of the circle. ∠ ABC = 45° and AC = 7 cm. Find the area of segment BXC.
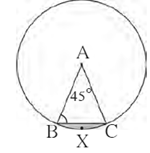
As per data given in question, fig is as below.

The radius (r) of the circle = AC = 7 cm.
In Δ ABC,
seg AB ≅ seg AC …(Radii of the same circle)
∴ ∠ ABC ≅ ∠ ACB ... (Isosceles triangle theorem)
∠ ABC = ∠ ACB = 45°
In Δ ABC,
∠ ABC + ∠ ACB + ∠ BAC =180° ... (Sum of all angles of a triangle is 180°)
∴ 45° + 45° + ∠BAC = 180°
∴ 90° + ∠ BAC = 180°
∴ ∠ BAC =180° − 90°
∴ ∠ BAC = 90°
m(arc BXC) = ∠ BAC = θ = 90° ... (Definition of measure of minor arc)
A(segment BXC) = r2 \([\frac{πθ}{360}-\frac{sin\,θ}{2}]\)
= \((7\sqrt{2})^2[\frac{3.14×90}{360}-\frac{sin\,90}{2}]\)
= 98 × \([\frac{3.14}{4}-\frac{1}{2}]\) …. ( sin 90° = 1)
= 98 × \(\frac{1.14}{4}\) = 27.93 cm2
Answer is : A(segment BXC) = 27.93 cm2
[Note : In the question, if ∠ ABC =45°, then the area of segment BXC is 27.93 cm2 and not 3.72 cm2 as given in the textbook but if we consider ∠ BAC = 45° instead of ∠ ABC = 45° then area of segment BXC will be 3.92 cm2 which is near to 3.72 cm2 as given in the textbook, if ∠ BAC = 45° then solution would be as follows.]
The radius (r) of the circle = AC = 7 cm.
m(arc BXC) = ∠ BAC = θ = 45°

A(segment BXC) = r2\([\frac{πθ}{360}-\frac{sin\,θ}{2}]\)
= \((7\sqrt{2})^2[\frac{3.14×45}{360}-\frac{sin\,45}{2}]\)
= 98 × \([\frac{3.14}{8}-\frac{1}{2\sqrt{2}}]\) …. ( sin 45° = \(\frac{1}{\sqrt{2}}\) )
= 98 × \([\frac{0.32}{8}]\) = 3.92 cm2
Answer is : A(segment BXC) = 3.92 cm2
Question 4.2. In the figure, O is the centre of the circle. m(arc PQR) = 60° OP = 10 cm. Find the area of the shaded region. (π = 3.14, = 1.73)
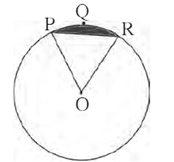
The radius (r) of the circle = OP =10 cm.
m(arc PQR) = θ = 60°.
The shaded region is segment PQR,
A (segment PQR) = r2\([\frac{πθ}{360}-\frac{sin\,θ}{2}]\)
= 102\([\frac{3.14×60}{360}-\frac{sin\,60}{2}]\)
= 102\([\frac{3.14}{6}-\frac{\sqrt{3}}{2×2}]\) …. ( sin 60° = \(\frac{\sqrt{3}}{2}\))
= 100 × \(\frac{1.09}{12}\) … …(as \(\sqrt{3}\) = 1.732)
= \(\frac{109}{12}\) = 9.08 cm2
Answer is : Area of the shaded region is 9.08 cm2.
Question 4.3. In the figure, if A is the centre of the circle. ∠ PAR = 30°, AP = 7.5, find the area of the segment PQR (π = 3.14)
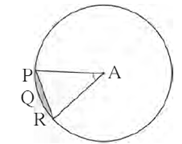
The radius (r) of the circle = AP =7.5.
m(arc PQR) = ∠ PAR = θ =30°.
Area of the segment PQR = r2\([\frac{πθ}{360}-\frac{sin\,θ}{2}]\) = 7.52\([\frac{3.14×30}{360}-\frac{sin\,30}{2}]\)
= 7.52\([\frac{3.14}{12}-\frac{1}{2×2}]\) …. ( sin 30° = \(\frac{1}{2}\))
= 7.52 \([\frac{0.14}{12}]\) = \(\frac{7.785}{12}\) = 0.65625 sq units
Answer is : Area of segment PQR is 0.65625 sq units.
Question 4.4. In the figure 7.46, if O is the centre of the circle, PQ is a chord. ∠ POQ = 90°, area of shaded region is 114 cm2, find the radius of the circle. (π = 3.14)
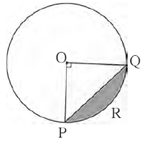
Area of the shaded region is 114 cm2.
The shaded region is segment PRQ.
A (segment PRQ) = 114 cm2
m (arc PRQ) = ∠ POQ = θ = 90°
A (segment PRQ) = r2\([\frac{πθ}{360}-\frac{sin\,θ}{2}]\)
∴ 114 = r2 \([\frac{3.14×90}{360}-\frac{sin\,90}{2}]\)
∴ 114 = r2 \([\frac{3.14}{4}-\frac{1}{2}]\)
∴ 114 = r2 \([\frac{1.14}{4}]\)
∴ r2 = \(\frac{114×4}{1.14}\) = 400
∴ r = 20 cm
Answer is : The radius of the circle is 20 cm.
Question 4.5. A chord PQ of a circle with radius 15 cm subtends an angle of 60° with the centre of the circle. Find the area of the minor as well as the major segment. (π = 3.14, = 1.73)
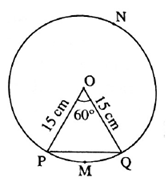
Let the centre of the circle be O.
Consider points M and N as shown. The radius of
the circle (r) = 15 cm.
m(arc PMQ) = ∠ POQ = θ = 60°
Area of the minor segment = r2\([\frac{πθ}{360}-\frac{sin\,θ}{2}]\) = 152 \([\frac{3.14×60}{360}-\frac{sin\,60}{2}]\)
= 225\([\frac{3.14}{6}-\frac{\sqrt{3}}{2×2}]\) = 225\([\frac{3.14}{6}-\frac{1.73}{4}]\) = 225\([\frac{1.09}{12}]\) = 20.43 cm2
A(circle) = πr2
= 3.14 × 15 × 15
= 3.14 × 225
= 706.5 cm2
A(major segment) = A(circle) − A(minor segment)
= 706.5 − 20.43
= 686.07 cm2
Answer is : A(minor segment) is 20.43 cm2 and A (major segment) is 686.07 cm2.
PDF-Notes,Solution,Text Book
PDF : Class 10th-Mathematics-2-Chapter-7-Mensuration-Text Book
PDF : Class 10th-Mathematics-2-Chapter-7-Mensuration-Notes
PDF : Class 10th-Mathematics-2-Chapter-7-Mensuration-Solution
All Chapters Notes-Class-10-Mathematics-1 and 2- (13 PDF)
All Chapters Solutions-Class-10-Mathematics-1 and 2- (13 PDF)
All Chapters Notes + Practice Set Solutions-Class-10-Mathematics-1 and 2- (26 PDF)
Main Page : – Maharashtra Board Class 10th-Mathematics – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter-6-Trigonametry – Online Solutions
We reply to valid query.