Circle
Class-10-Mathematics-2-Chapter-3-Maharashtra Board
Solutions
Practice set 3.1
Question 1.1. In the adjoining figure the radius of a circle with centre C is 6 cm, line AB is a tangent at A. Answer the following questions.

(1) What is the measure of ∠ CAB? Why ?
(2) What is the distance of point C from line AB? Why ?
(3) d(A, B) = 6 cm, find d(B, C).
(4) What is the measure of ∠ ABC? Why ?
(1) ∠ CAB = 90° ... (Tangent theorem) ... (1)
(2) seg CA ⊥ line AB
CA = 6 cm ... (Given)
∴ C is at a distance of 6 cm from line AB.
(3) In Δ CAB,
∠ CAB = 90° ... [From (1)]
∴ by Pythagoras theorem,
CB2 = CA2 + AB2
∴ BC2 = 62 + 62
∴ BC2 = 36 + 36 = 72
∴ BC = 6\(\sqrt{2}\) cm ... (Taking square roots of both the sides)
d(B,C) = BC = 6\(\sqrt{2}\) cm.
(4) In Δ ABC,
CA = AB ... (Each is the length 6 cm)
∠ ABC = ∠ ACB ... (Isosceles triangle theorem)
Let ∠ ABC = ∠ ACB = x°
In Δ ABC,
∠ CAB + ∠ ABC + ∠ ACB = 180° ... (Sum of all angles of a triangle is 180°)
∴ 90° + x° + x° = 180°
∴ 2x° = 180°— 90°
∴ 2x° = 90°
∴ x° = 90°/2
∴ x° = 45°
∴ ∠ ABC = 45°.
Answer :
(1) ∠ CAB= 90°,
(2) C is at a distance of 6 cm from line AB,
(3) d(B, C) = 6\(\sqrt{2}\) cm and
(4) ∠ ABC = 45°.
Question 1.2. In the adjoining figure, O is the centre of the circle. From point R, seg RM and seg RN are tangent segments touching the circle at M and N.
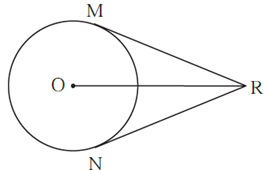
If (OR) = 10 cm and radius of the circle = 5 cm, then
(1) What is the length of each tangent segment ?
(2) What is the measure of ∠ MRO ?
(3) What is the measure of ∠ MRN ?
Draw seg OM and seg ON.
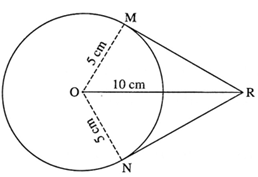
(1) In Δ OMR,
∠ OMR = 90° ... (Tangent theorem)
∴ by Pythagoras theorem,
OR2 = OM2 + MR2
∴ 102 = 52 + MR2
∴ MR2 = 100 — 25
∴ MR2 = 75
∴ MR = 5\(\sqrt{3}\) cm ... (Taking square roots of both the sides)
RM = RN = 5\(\sqrt{3}\) cm ... (Tangent segment theorem)
Length of each tangent segment is 5\(\sqrt{3}\) cm. ... (Given)
(2) In Δ RMO, ∠ OMR = 90° ... (Tangent theorem)
OM = 5 cm and OR = 10 cm
∴ OM = \(\frac{1}{2}\)OR
∴ ∠ MRO = 30° ... (Converse of 30°—60°—90° triangle theorem)
Similarly ∠ NRO = 30°
(3) ∠ MRN = ∠ MRO + ∠ NRO ... (Angle addition postulate)
∴ ∠ MRN = 30°+ 30°
∴ ∠ MRN= 60°
Answer :
(1) Length of each tangent segment is 5\(\sqrt{3}\) cm,
(2) ∠ MRO = 30°
(3) ∠ MRN = 60°.
Question 1.3. Seg RM and seg RN are tangent segments of a circle with centre O. Prove that seg OR bisects ∠ MRN as well as ∠ MON.
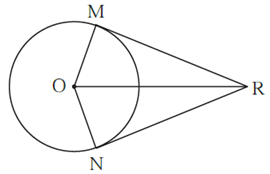
Proof : In Δ RMO and Δ RNO
∠ RMO = ∠ RNO = 90° ... (Tangent theorem)
Hypotenuse OR ≅ hypotenuse OR ... (Common side)
Side OM ≅ side ON ... (Radii of the same circle)
∴ Δ RMO ≅ Δ RNO ... (Hypotenuse side theorem)
∴ ∠ MRO ≅ ∠ NRO and ∠ MOR ≅ ∠ NOR ... (c.a.c.t.)
∴ seg OR bisects ∠ MRN and ∠ MON.
Question 1.4. What is the distance between two parallel tangents of a circle having radius 4.5 cm ? Justify your answer.
Let the centre of the circle be O. Let the tangents AB and CD touch the circle at points M and N respectively.

Draw seg OM and seg ON.
Through O, draw line XY || line AB
Line AB || line CD ... (Given)
Line XY || line AB ... (Construction)
∴ line AB || line XY || line CD ... (1)
∠ OMA = ∠ ONC = 90° ... (Tangent theorem)
Line AB || line XY and line MO is the transversal,
∠ AMO + ∠ MOX = 180° ... (Interior angles theorem)
∴ 90°+ ∠ MOX = 180°
∴ ∠ MOX = 180°— 90°
∴ ∠ MOX = 90°
Similarly ∠ NOX = 90°
∴ ∠ MOX + ∠ NOX = 90° + 90° = 180°
∴ ∠ MOX and ∠ NOX are adjacent as well as supplementary.
∴ ∠ MOX and ∠ NOX form linear pair.
∴ ray OM and ray ON are opposite rays.
∴ points M, O and N are collinear.
∴ MN is the distance between the parallel tangents AB and CD
MN = 2 × radius ... (Diameter is twice the radius)
∴ MN =2 × 4.5
∴ MN = 9 cm
Answer : Distance between parallel tangents is 9 cm.
Practice set 3.2
Question 2.1. Two circles having radii 3.5 cm and 4.8 cm touch each other internally. Find the distance between their centres.
Let the radii of the two circles be r1 and r2.
r1 = 3.5 cm and r2 = 4.8 cm ... (Given)
The two circles are touching each other internally.
∴ by theorem of touching circles, the centres and the point of contact are collinear.
The distance between the centres of the circles touching internally is equal to the difference of their radii
∴ distance between their centres = r2 — r1 = 4.8 — 3.5 = 1.3 cm.
Answer : Distance between the centres is 1.3 cm.
Question 2.2. Two circles of radii 5.5 cm and 4.2 cm touch each other externally. Find the distance between their centres.
Let the radii of the two circles be r1 and r2.
r1 = 5.5 cm and r2 = 4.2 cm ... (Given)
The two circles are touching each other externally
∴ by theorem of touching circles, the centres and the point of contact are collinear.
The distance between the centres of the circles touching externally is equal to the sum of their radii.
∴ distance between their centres = r1 + r2 = 5.5 + 4.2 = 9.7 cm
Answer : Distance between the centres is 9.7 cm.
Question 2.3. If radii of two circles are 4 cm and 2.8 cm. Draw figure of these circles touching each other — (i) externally (ii) internally.
(i) Circles touch each other externally.

(i) Circles touch each other internally.

Question 2.4. In fig 3.27, the circles with centres P and Q touch each other at R. A line passing through R meets the circles at A and B respectively.
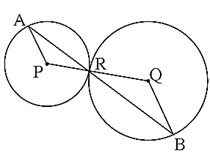
Prove that —
(1) seg AP || seg BQ,
(2) Δ APR ~ Δ RQB, and
(3) Find ∠ RQB if ∠ PAR = 35°
(1) P—R—Q ... (By theorem of touching circles)
In Δ PAR,
seg PA ≅ seg PR ... (Radii of the same circle)
∴ ∠ PAR ≅ ∠ PRA ... (Isosceles triangle theorem) ... (1)
In Δ QRB,
seg QR ≅ seg QB ... (Radii of the same circle)
∴ ∠ QRB ≅ ∠ QBR ... (Isosceles triangle theorem) ... (2)
∠ PRA ≅ ∠ QRB ... (Vertically opposite angles) ... (3)
∴ from (1). (2) and (3), we get,
∠ PAR ≅ ∠ QBR
i.e. ∠ PAB ≅ ∠ QBA ... (A—R—B)
∴ seg AP || seg BQ ... (Alternate angles test for parallel lines)
(2) In Δ APR and Δ RQB,
∠ PAR ≅ ∠ QRB ... [From (1) and (3)]
∠ PRA ≅ ∠ QBR ... [From (2) and (3)]
∴ Δ APR ~ Δ RQB ... (AA test of similarity)
(3) ∠ PAR = 35° ... (Given)
∴ from (1), (2) and (3),
∠ PRA = ∠ QRB = ∠ QBR = 35° ... (4)
In Δ QRB,
∠ QRB + ∠ QBR + ∠ RQB = 180° ... (Sum of all angles of a triangle is 180°)
∴ 35° + 35° + ∠ RQB = 180° ... [From (4)]
∴ 70° + ∠ RQB = 180°
∴ ∠ RQB = 180°— 70°
∴ ∠ RQB = 110°
∠ RQB = 110°.
Question 2.5. In fig the circles with centres A and B touch each other at E. Line l is a common tangent which touches the circles at C and D respectively. Find the length of seg CD if the radii of the circles are 4 cm, 6 cm.
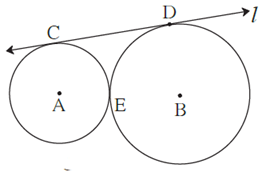
Draw seg AC, seg BD and seg AB. Draw seg AM ⊥ seg BD and B—M—D.
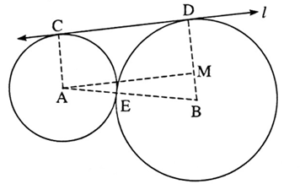
A—E—B ... (By theorem of touching circles)
AE = AC = 4 cm and BE = BD =6 cm ... (Radii of the same circle)
∠ ACD = ∠ BDC = 90° ... (Tangent theorem) ... (1)
In □ AMDC,
∠ ACD + ∠ CDM + ∠ AMD + ∠ CAM = 360° … (Sum of all angles of quadrilateral is 360°)
∴ 90° + 90° + 90° + ∠ CAM = 360° [From construction, (1) and B—M—D]
∴ 270° + ∠ CAM = 360°
∴ ∠CAM = 360° — 270°
∴ ∠ CAM = 90°
∴ □ AMDC is a rectangle ….(By definition)
∴ DM = AC = 4 cm ….. (Opposite sides of rectangle are equal)
BM + MD = BD ….(B—M—D)
∴ BM + 4 = 6
∴ BM = 6 — 4
∴ BM = 2 cm.
∴AB =AE + EB (A—E—B)
∴AB = 4 + 6
∴AB = 10 cm.
In Δ AMB, ∠ AMB = 90°. …..(Construction)
∴ by Pythagoras theorem,
AB2 = AM2 + BM2
∴ 102 = AM2 + 22
∴ AM2 = 102 — 22
∴ AM2 = 100—4 ∴ AM2 = 96 = 16 × 6
∴ AM = 4 cm …. (Taking square roots of both the sides)
CD = AM …. (Opposite sides of rectangle are equal)
∴ CD = 4 cm
Answer : CD = 4 cm.
Practice set 3.3
Question 3.1. In figure, points G, D, E, F are concyclic points of a circle with centre C. ∠ ECF = 70°, m(arc DGF) = 200° find m(arc DE) and m(arc DEF).
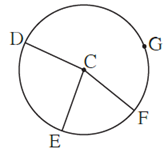
m(arc EF) = ∠ ECF … (Definition of measure of minor arc)
∠ ECF = 70° ….(Given)
∴ m(arc EF) = 70°
m(arc DGF) + m(arc EF) + m(arc DE) = 360° …. (Measure of a circle is 360°)
∴ 200° + 70° + m(arc DE) = 360°
∴ 270° + m(arc DE) = 360°
∴ m(arc DE) = 360° — 270°
∴ m(arc DE) = 90°
m(arc DE) + m(arc EF) = m(arc DEF) ….. (Arc addition postulate)
∴ 90° + 70° = m(arc DEF)
∴ m(arc DEF) = 160°
Answer : m(arc DE) = 90° and m(arc DEF) = 160°.
Question 3.2. In fig Δ QRS is an equilateral triangle.
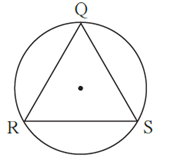
Prove that,
(1) arc RS ≅ arc QS ≅ arc QR
(2) m(arc QRS) = 240°.
Proof : Δ QRS is an equilateral triangle …..(given)
seg RS ≅ seg QS ≅ seg QR … (Sides of an equilateral triangle)
Arcs of the same circle are equal, if the related chords are congruent.
∴ arc RS ≅ arc QS ≅ are QR.
Let m(arc RS) = m(arc QS) = m(arc QR) = x ….(1)
m(arc RS) + m(arc QS) + m(arc QR) = 360° …..(Measure of a circle is 360°)
x + x + x = 360° ….[From (1)]
3x = 360°
x = 360°/3
∴ x = 120°
∴ m(arc RS) = m(arc QS) = m(arc QR) = 120°
∴ m(arc QRS) = m(arc QR) + m(arc RS) …. (Arc addition postulate)
∴ m(arc QRS) = 120° + 120°
∴ m(arc QRS) = 240°.
Question 3.3. In fig chord AB ≅ chord CD, Prove that, arc AC ≅ arc BD
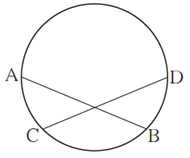
Chord AB ≅ chord CD (Given)
∴ Arc ACB ≅ arc CBD …. (Arcs corresponding to congruent chords)
∴ m(arc ACB) = m(arc CBD) …..(1)
But m(arc ACB) = m(arc AC) + m(arc CB) …..(2)
and m(arc CBD) = m(arc CB) + m(arc BD) …..(3)
From (1), (2) and (3), We get,
m(arc AC) + m(arc CB) = m(arc CB) + m(arc BD)
∴ m(arc AC) = m(arc BD)
∴ arc AC ≅ arc BD.
Practice set 3.4
Question 4.1. In figure, in a circle with centre O, length of chord AB is equal to the radius of the circle.
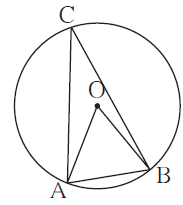
Find measure of each of the following.
(1) ∠ AOB (2) ∠ ACB (3) arc AB (4) arc ACB.
Seg OA ≅ seg OB ….(Radii of the same circle)
chord AB is equal to radius ….(Given)
∴ seg AB ≅ seg OA ≅ seg OB
∴ Δ AOB is an equilateral triangle.
∴ ∠ AOB = 60° ….. (Angle of an equilateral triangle)
The measure of an angle subtended by an arc at a point on the circle is half of the measure of the angle subtended by the arc at the centre.
∴ ∠ ACB = \(\frac{1}{2}\)∠ AOB
∴ ∠ ACB = \(\frac{60^0}{2}\)
∴ ∠ ACB = 30°
m(arc AB) = ∠ AOB ……(Definition of measure of a minor arc)
∴ m(arc AB) = 60°
m(arc AB) + m(arc ACB) = 360° ….. (Measure of a circle is 360°)
∴ 60° + m(arc ACB) = 360°
∴ m(arc ACB) = 360° — 60°
∴ m(arc ACB) = 300°.
Answer :
(1) ∠ AOB = 60°,
(2) ∠ ACB = 30°,
(3) m(arc AB) = 60°
(4) m(arc ACB) = 300°.
Question 4.2. In figure, □ PQRS is cyclic. side PQ ≅ side RQ. ∠ PSR = 110°,
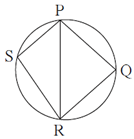
Find—
(1) measure of ∠ PQR
(2) m(arc PQR)
(3) m(arc QR)
(4) measure of ∠ PRQ
(1) □ PQRS is cyclic.
∠ PSR + ∠ PQR = 180° .(Opposite angles of cyclic quadrilateral are supplementary)
∴ 110° + ∠ PQR = 180°
∴ ∠ PQR = 180° — 110°
∴ ∠ PQR = 70°
(2) ∠ PSR = \(\frac{1}{2}\) m(arc PQR) ……(Inscribed angle theorem)
110° = m(arc PQR)
∴ m(arc PQR) = 110° × 2
∴ m(arc PQR) = 220°
(3) Chord PQ ≅ chord QR …..(Given)
arc PQ ≅ arc QR ……(Arcs corresponding to congruent chords)
Let m(arc PQ) = m(arc QR) = x
m(arc PQ) + m(arc QR) = m(arc PQR) …..(Arcs addition postulate)
∴ x + x = 220
∴ 2x = 220
∴ x = \(\frac{220}{2}\)
∴ x = 110°
m(arc QR) = 110° and m(arc PQ) = 110°
(4) ∠ PRQ = \(\frac{1}{2}\) m(arc PQ) ……(Inscribed angle theorem)
∠ PRQ = \(\frac{1}{2}\) × 110°
∠ PRQ = 55°.
Answer :
(1) ∠ PQR = 70°,
(2) m(arc PQR) = 220°,
(3) m(arc QR) = 110°
(4) ∠ PRQ= 55°.
Question 4.3. □ MRPN is cyclic, ∠ R = (5x — 13)°, ∠ N = (4x + 4)°. Find measures of ∠ R and ∠ N.
□ MRPN is cyclic ….(Given)
by theorem of cyclic quadrilateral,
∠ R + ∠ N = 180°
∴ (5x — 13)° + (4x + 4)° = 180°
∴ 5x – 13 + 4x + 4 = 180
∴ 9x — 9 = 180
∴ 9x = 180 + 9
∴ 9x = 189
∴ x = \(\frac{189}{9}\)
∴ x = 21
∠ R = 5x — 13
∠ R = 5(21) — 13
∠ R = 105 — 13, ∴ ∠ R = 92
∠ N = (4x + 4)
∠ N = 4(21) + 4
∠ N = 84 + 4 ∴ ∠ N = 88°
Answer : ∠ R = 92° and ∠ N = 88°.
Question 4.4. In figure, seg RS is a diameter of the circle with centre O. Point T lies in the exterior of the circle.
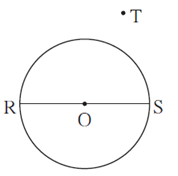
Prove that : ∠ RTS is an acute angle.
Proof : Let seg RT intersect circle at point M. Draw seg MS.
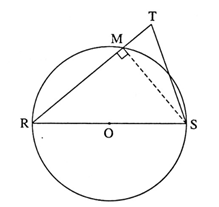
Angle inscribed in a semicircle is a right angle
∴ ∠ RMS = 90°
∴ seg SM ⊥ side RT
∴ Δ TMS is a right angled triangle.
∴ ∠ TMS + ∠ MTS + ∠ TSM = 180° …. (Sum of all angles of a triangle is 180°)
∴ 90° + ∠ MTS + ∠ TSM = 180°
∴ ∠ MTS + ∠ TSM = 180° — 90°
∴ ∠ MTS + ∠ TSM = 90°
∴ ∠ MTS < 90°
i.e. ∠ RTS < 90° (R—M—T)
∴ ∠ RTS is an acute angle (By definition)
Question 4.5. Prove that, any rectangle is a cyclic quadrilateral
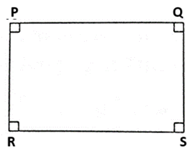
Given : □ PQRS is rectangle.
To prove : □ PQRS is a cyclic quadrilateral.
Proof : □ PQRS is a rectangle. …..(Given)
∴ ∠ P = ∠ Q = ∠ R = ∠ S = 90° ….. (Angles of a rectangle)
∠ P + ∠ S = 90° + 90° = 180°
∴ PQRS is a cyclic quadrilateral. …. (By converse of cyclic quadrilateral theorem)
Question 4.6. In figure, altitudes YZ and XT of Δ WXY intersect at P.
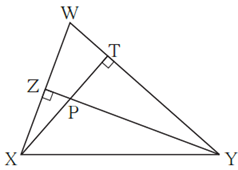
Prove that,
(1) □ WZPT is cyclic.
(2) Points X, Z, T, Y are concyclic.
∠ WZP = ∠ WTP = 90° ….(Given)
∴ ∠ WZP + ∠ WTP = 90° + 90° = 180°
∴ by converse of cyclic quadrilateral theorem,
□ WZPT is cyclic.
∠ XZY = ∠ XTY = 90° ….(Given)
∴ points X and Y on line XY subtend equal angles at two distinct points Z and T on the same side of line XY.
If two points on a given line subtend equal angles at two distinct points which lie on the same side of the line, then the four points are concyclic.
∴ Points X, Z, T, Y are concyclic.
Question 4.7. In figure, m(arc NS) = 125°, m(arc EF) = 37°, find the measure ∠ NMS.
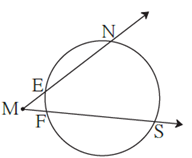
m(arc NS) = 125°, m(arc EF) = 37° …(Given)
∠ NMS has its vertex in the exterior of the circle and intercepts arc EF and arc NS.
∴ ∠ NMS = \(\frac{1}{2}\) [m(arc NS) — m(arc EF)]
∴ ∠ NMS = \(\frac{1}{2}\) × [125°— 37°]
∴ ∠ NMS = \(\frac{1}{2}\) × 88° ∴ ∠ NMS = 44°
Answer : ∠ NMS = 44°.
Question 4.8. In figure, chords AC and DE intersect at B. If ∠ ABE = 108°, m(arc AE) = 95°, find m(arc DC) .
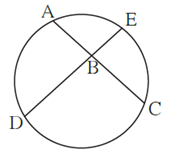
m(arc AE) = 95°, ∠ ABE = 108° (Given)
∠ ABE has its vertex inside the circle and intercepts arc AE and its vertically opposite
∠ DBC intercepts arc DC.
∠ ABE = \(\frac{1}{2}\) [m(arc AE) + m(arc 130)]
∴ 108° = \(\frac{1}{2}\) × [95° + m(arc 130)]
∴ 108° × 2 = 95° + m(arc DC)
∴ 216° = 95° + m(arc DC)
∴ m(arc DC) = 216° — 95°
∴ m(arc DC) = 121°
Answer : m(arc DC) = 121°.
Practice set 3.5
Question 5.1. In figure, ray PQ touches the circle at point Q. PQ = 12, PR = 8, find PS and RS.
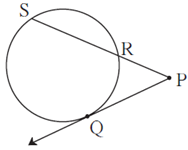
Ray PQ is tangent touching the circle at point Q and line PRS is secant intersecting the circle at points R and S.
∴ PQ2 = PR × PS ….. (By tangent secant segments theorem)
∴ 122 = 8 × PS
∴ PS = \(\frac{12×12}{8}\)
∴ PS = 18
PR + RS = PS ….(P—R—S)
∴ 8 + RS = 18
∴ RS = 18 — 8
∴ RS = 10
Answer : PS = 18 and RS = 10.
Question 5.2. In figure, chord MN and chord RS intersect at point D.
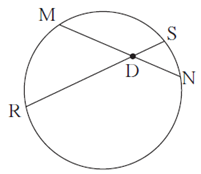
(1) If RD = 15, DS = 4, MD = 8 find DN
(2) If RS = 18, MD = 9, DN = 8 find DS
Chords MN and RS intersect each other at point D inside the circle.
∴ by theorem of internal division of chords,
DM × DN = DR × DS
∴ 8 × DN = 15 × 4
∴ DN = \(\frac{15×4}{8}\)
∴ DN = 7.5
Answer : DN = 7.5.
Let DS = x
DR + DS = RS …..(R—D—S)
∴ DR + x = 18
∴ DR = (18 —x)
Chords MN and RS intersect each other at point D inside the circle.
∴ by theorem of internal division of chords,
DM × DN = DR × DS
∴ 9 × 8 = (18 — x) × x
∴ 72 = 18x — x2
∴ x2 — 18x + 72 = 0
∴ x2 — 12x— 6x + 72 = 0
x(x — 12) — 6(x — 12) = 0
(x — 12)(x — 6) = 0
Either x—12 = 0 or x – 6 = 0
∴ x = 12 or x = 6
DS = 12 or DS = 6
Answer : DS = 12 or DS = 6.
Question 5.3. In figure, O is the centre of the circle and B is a point of contact. seg OE ⊥ seg AD, AB = 12, AC = 8, find (1) AD (2) DC (3) DE.
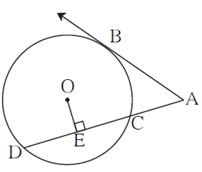
Ray AB is tangent to the circle at point B. Line ACD is secant intersecting the circle at points C and D.
∴ by tangent secant segments theorem,
AB2 = AC × AD
∴ 122 = 8 × AD
∴ AD = \(\frac{12×12}{8}\)
∴ AD = 18
AC + CD = AD ….(A—C—D)
∴ 8 + CD = 18
∴ CD = 18 — 8
∴ CD = 10
seg OE ⊥ chord CD (Given)
Perpendicular drawn from the centre of the circle to the chord bisects the chord.
∴ DE = \(\frac{1}{2}\) × CD, ∴ DE = \(\frac{1}{2}\) × 10 = 5
∴ DE = 5
Answer :
(1) AD = 18,
(2) DC = 10
(3) DE = 5.
Question 5.4. In figure, if PQ = 6, QR = 10, PS = 8 find TS.
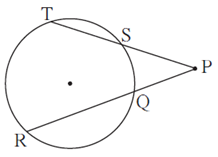
PR = 6 + 10
PR = 16
Chord ST and chord QR intersect at point P outside the circle.
∴ by theorem of external division of chords,
PS × PT = PQ × PR
∴ 8 × PT = 6 × 16
∴ PT = \(\frac{6×16}{8}\)
∴ PT = 12
PS + TS = PT …(P—S—T)
∴ 8 + TS = 12
∴ TS = 12 — 8
∴ TS = 4
Answer : TS = 4.
Question 5.5. In figure, seg EF is a diameter and seg DF is a tangent segment. The radius of the circle is r. Prove that, DE × GE = 4r2
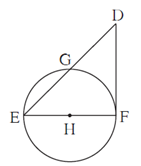
Proof :
Line DF is tangent to the circle touching the circle at point F and line DGE is secant intersecting the circle at points G and E.
∴ by tangent secant segments theorem,
DF2 = DG × DE ……(1)
In Δ DFE,
∠ DFE = 90° …..(By tangent theorem)
∴ by Pythagoras theorem,
DE2 = DF2 + EF2
∴ DE2 = DF2 + (2r)2 ….(∵ Diameter is twice the radius)
∴ DE2 = DF2 + 4r2
∴ 4r2 = DE2 — DF2
∴ 4r2 = DE2 — DG × DE ….[From (1)]
∴ 4r2 = DE (DE — DG)
∴ 4r2 = DE × GE …(D—G—E)
∴ DE × GE = 4r2.
PDF-Notes,Solution,Text Book
Main Page : – Maharashtra Board Class 10th-Mathematics – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter-2-Pythagoras Theorem – Online Solution
Next Chapter : Chapter-4-Geometric Construction – Online Solution