3² = 9, 5² = 25, 4² = 16

∴ 3² + 4² = 9 + 16 = 25

∴ 3² + 4² = 5²

The square of the largest number is equal to the sum of the squares of the other two numbers.

∴ (3, 5, 4) is a Pythagorean triplet.

4² = 16, 9² = 81, 12² = 144

∴ 4² + 9² = 16 + 81 = 97

∴ 4² + 9² ≠ 12²

The square of the largest number is not equal to the sum of the squares of the other two numbers.

∴ (4, 9, 12) is not a Pythagorean triplet.

5² = 25, 12² = 144, 13² = 169

∴ 5² + 12² = 25 + 144 = 169

∴ 5² + 12² = 13²

The square of the largest number is equal to the sum of the squares of the other two numbers.

∴ (5, 12, 13) is a Pythagorean triplet.

24² = 576, 70² = 4900, 74² = 5476

∴ 24² + 70² = 576 + 4900 = 5476

∴ 24² + 70² = 74²

The square of the largest number is equal to the sum of the squares of the other two numbers.

∴ (24, 70, 74) is a Pythagorean triplet.

10² = 100, 24² = 576, 27² = 729

∴ 10² + 24² = 100 + 576 = 676

∴ 10² + 24² ≠ 27²

The square of the largest number is not equal to the sum of the squares of the other two numbers.

∴ (10, 24, 27) is not a Pythagorean triplet.

11² = 121, 60² = 3600, 61² = 3721

∴ 11² + 60² = 121 + 3600 = 3721

∴ 11² + 60² = 61²

The square of the largest number is equal to the sum of the squares of the other two numbers.

∴ (11, 60, 61) is a Pythagorean triplet.

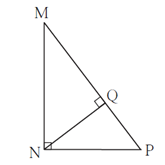
In Δ MNP,

A MNP = 90°          …..(Given)

seg NQ ⊥ hypotenuse MP

by theorem of geometric mean.

NQ² = MQ × PQ

∴ NQ² = 9 × 4

∴ NQ² = 36

∴ NQ = 6    ….  (Taking square roots of both the sides)

Answer is : NQ = 6.

In Δ QPR,

∠ QPR = 90°       …..(Given)

seg PM ⊥ hypotenuse QR     …..(Given)

by theorem of geometric mean,

PM² = QM × MR

∴ 10² = 8 × MR

∴ MR = 100/8

∴ MR = 12.5

QR = QM + MR  (Q—M—R)

∴ QR = 8 + 12.5  = 20.5

Answer is : QR = 20.5.

In Δ PSR,

∠ PSR = 90°     ……(Given)

∠ SPR = 30°

∠ SRP = 60°     ……(Remaining angle of a triangle)

Δ PSR is a 30°— 60°— 90° triangle.

by 30°— 60°— 90° triangle theorem,

SR = \(\frac{1}{2}\)RP              …..(Side opposite to 30°)

∴ 6 = \(\frac{1}{2}\) × RP

∴ RP = 6 × 2  = 12

PS = \(\frac{\sqrt{3}}{2}\)RP                 ……(Slde opposite to 60°)

∴ PS = \(\frac{\sqrt{3}}{2}\) × 12

∴ PS = \(6\sqrt{3}\)

Answer is : RP = 12 and PS = \(6\sqrt{3}\)

AB = BC ……. (given )

∴ ∠ BAC = 45°

∴ AB = BC  = \(\frac{1}{\sqrt{2}}\) × AC

                  = \(\frac{1}{\sqrt{2}}\) × \(\sqrt{8}\)

                  = \(\frac{1}{\sqrt{2}}\) × \(2\sqrt{2}\)

                  = 2

Let □ ABCD be the given square and AC = diagonal = 10 cm

Let the side of the square be x cm.

∴ AB = BC = x cm.

In Δ ABC,

∠ ABC = 90°     ……(Angle of a square)

by Pythagoras theorem,

AC² = AB² + BC²

10² = x² + x²

100 = 2x²

x² = 100/2 = 50

∴ x² = 50

∴ x = \(5\sqrt{2}\)

∴ AB = \(5\sqrt{2}\) cm.

∴ side of square is \(5\sqrt{2}\) cm.

Perimeter of a square = 4 × side

= 4 × \(5\sqrt{2}\)

= \(20\sqrt{2}\) cm

Answer is :  Side of a square is \(20\sqrt{2}\)  cm and its perimeter is  cm.

(1) In Δ DFE,

∠ DFE = 90°       …..(Given)

seg FG ⊥ hypotenuse DE     ….(Given)

∴ by theorem of geometric mean,

FG² = DG × EG

12² = 8 × EG

∴ EG = 144/8 = 18

∴ EG = 18

(2) In Δ DGF,

∠ DGF = 90°      …..(Given)

∴ by Pythagoras theorem,

FD² = DG² + GF²

∴ FD² = 8² + 12²

∴ FD² = 64 + 144 = 208

∴ FD² = 208

∴ FD = \(4\sqrt{13}\)    ….  (Taking square roots of both the sides)

(3) In Δ EGF,

∠ EFG = 90°       …..(Given)

∴ by Pythagoras theorem,

EF² = EG² + GF²

∴ EF² = 18² +12²

∴ EF² = 324 + 144

∴ EF² = 468

EF = \(6\sqrt{13}\)     …..  (Taking square roots of both the sides)

Answer is :  (1) EG = 18 (2) FD = \(4\sqrt{13}\)  and (3) EF = \(6\sqrt{13}\) .

Let □ PQRS be the given rectangle (fig.). QR = 35 cm, RS = 12 cm.

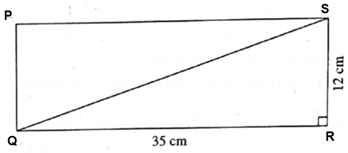
In Δ QRS,

∠ QRS = 90°       …..(Angle of a rectangle)

∴ by Pythagoras theorem,

QS² = QR² + RS²

∴ QS² = 35² + 12²

∴ QS² = 1225 + 144

∴ QS² = 1369

∴ QS = 37 cm       ….. (Taking square roots of both the sides)

Answer is : The diagonal of rectangle is 37 cm.

Proof : In Δ PRQ,

∠ PRQ = 90°      …..(Given)

∴ by Pythagoras theorem,

PQ² = PR² + QR²     …..(1)

In Δ PRM,

∠ PRM = 90°     …..(Given)

∠ by Pythagoras theorem,

PM² = PR² + RM²          …..(2)

RM = \(\frac{1}{2}\)RQ            ….(M is the midpoint of seg RQ)  ….(3)

∴ PM² = PR² + \((\frac{1}{2}RQ)^2\)          ….[From (2) and (3)]

PM² = PR² +  RQ²

Multiplying each term with 4, we get,

4PM² = 4PR² + \(\frac{1}{4}\)RQ²

4PM² = 3PR² + (PR² + RQ²)

4PM² = 3PR² + PQ²          ….[From (1)]

4PM² — 3PR² = PQ²          OR

PQ² = 4PM² — 3PR²  …proved.

In the figure, seg XB and seg YD represent the walls of two buildings on either side of a street BD.

Seg AC represents the first position of the ladder and seg CE represents the second position of the ladder.

AC = CE = 5.8 m, AB = 4 m and DE = 4.2 m.

In Δ ABC, ∠ ABC = 90°.

∴ by Pythagoras theorem,

AC² = AB² + BC²

5.8² = 4² + BC²

33.64 = 16 + BC²

BC² = 33.64 — 16

∴ BC² = 17.64

BC = 4.2 m      … (Taking square roots of both the sides)

In Δ EDC, ∠ EDC = 90°.

∴ by Pythagoras theorem,

CE² = DE² + CD²

5.8² = 4.2² + CD²

CD² = 5.8² — 4.2²

CD² = 33.64 — 17.64

∴ CD² = 16

∴  CD = 4 m     …. (Taking square roots of both the sides)

BD = BC + CD  (B—C—D)

BD = 4.2 + 4

 BD = 8.2 m

Answer is : Width of the street is 8.2 m

In Δ PQR, seg PS is the median  …..(By definition)

∴ by Apollonius theorem,

PQ² + PR² = 2PS² + 2QS²

∴ 11² + 17² = 2(13)² + 2QS²

∴ 121 + 289 = 2 × 169 + 2QS²

∴ 410 = 388 + 2QS²

∴ 2QS² = 410 — 388

∴ 2QS² = 72

∴ QS² = 36

∴ QS = 6    ….  (Taking square roots of both the sides)

QS = \(\frac{1}{2}\)QR  (S is the midpoint of seg QR)

∴ 6 = \(\frac{1}{2}\)QR

∴ QR = 6 × 2

∴ QR = 12

Answer is : QR = 12

Let seg CM be the median drawn from the vertex C to side AB.

∴ M is the midpoint of side AB     …..(By definition of a median)

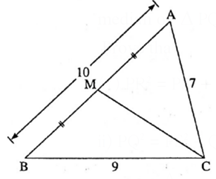
∴ AM = \(\frac{1}{2}\)AB = \(\frac{1}{2}\) × 10 = 5

In Δ ACB, seg CM is the median,

∴ by Apollonius theorem,

AC² + BC² = 2CM² + 2AM²

∴ 7² + 9² = 2CM² + 2(5) ²

∴ 49 + 81 = 2CM² + 50

∴ 130 – 50 = 2CM²

∴ CM² = 80/2 = 40

∴ CM =  \(2\sqrt{10}\)      …. (Taking square roots of both the sides)

Answer is : Length of the median drawn from point C to side AB is \(2\sqrt{10}\) 

Proof :  Seg PS is the median of Δ PQR      …..(Given)

QS = SR = \(\frac{1}{2}\)QR     ….. (S is the midpoint of side QR)  ….(1)

In Δ PTS, ∠ PTS = 90°       …..(Given)

∴ by Pythagoras theorem,

PS² = PT² + TS²      …..(2)

(1) In Δ PTR, ∠ PTR = 90°     …..(Given)

∴ by Pythagoras theorem,

PR² = PT² + TR²

∴ PR² = PT² + (TS + SR)²       …..(T—S—R)

∴ PR² = PT² + TS² + 2ST.SR + SR²      …. [(a + b)² = a² + 2ab + b²]

∴ PR² = (PT² + TS²) + 2ST.SR + SR²

∴ PR² = PS² + 2ST.\((\frac{QR}{2})\)+\((\frac{QR}{2})^2\)   ….. [From (1) and (2)]

∴ PR² = PS² + QR × ST + \((\frac{QR}{2})^2\) 

(2) In Δ PTQ, ∠ PTQ = 90°  (Given)

∴ by Pythagoras theorem,

PQ² = PT² + TQ²

∴ PQ² = PT² + (QS — TS)²              …(Q—T—S)

∴ PQ² = PT² + QS² — 2QS.TS + TS²    ….. [(a — b)² = a² — 2ab + b²]

∴ PQ² = (PT² + TS²) — 2QS.TS + QS²

∴ PQ² = PS² — 2\((\frac{QR}{2})\) × TS + \((\frac{QR}{2})^2\)      …..[From (1) and (2)]

PQ² = PS² — QR × ST + \((\frac{QR}{2})^2\)

In Δ ABC,  seg AM is the median.      ….(Given)

∴ by Apollonius theorem,

AB² + AC² = 2AM² + 2BM²

∴ 290 = 2(8) ² + 2BM²

290 = 128 + 2BM²

∴ 290 — 128 = 2BM²

∴ 2BM² = 162

∴ BM² = 162/2

∴ BM² = 81

∴ BM = 9 cm     … (Taking square roots of both the sides)

BM = \(\frac{1}{2}\)BC   …….(M is the midpoint of side BC)

∴ 9 = \(\frac{1}{2}\)BC

∴ BC = 18 cm

Answer is : BC = 18 cm.

Construction : Through T, draw seg AB || side SR such that A—T—B, P—A—S and  Q—B—R

Proof :

seg PS || seg QR      ….(Opposite sides of rectangle)

seg AS || seg BR       ……(P—A—S and Q—B—R)

also seg AB || seg SR     …..(Construction)

∴ □ ASRB is a parallelogram  (By definition)

∠ ASR = 90°               ……(Angle of rectangle PSRQ)

∴ □ ASRB is a rectangle    …. (A parallelogram is a rectangle, if one of its angles is a

right angle.)

∠ SAB = ∠ ABR = 90°             …..(Angles of a rectangle)

∴ seg TA ⊥ side PS and seg TB ⊥ side QR     ….(1)

AS = BR     …. (Opposite sides of rectangle are equal)  ….(2)

Similarly, we can prove AP = BQ  …..(3)

In Δ TAS,

∠ TAS = 90°       …..[From (1)]

∴ by Pythagoras theorem,

TS² = TA² + AS²     …..(4)

In Δ TBQ,

∠ TBQ = 90°           ….[From (1)]

∴ by Pythagoras theorem,

TQ² = TB² + BQ²     ……(5)

Adding (4) and (5), we get,

TS² + TQ² = TA² + AS² + TB² + BQ²      ….(6)

In Δ TAP,

∠ TAP = 90°  [From (1)]

∴ by Pythagoras theorem,

TP² = TA² + AP²     ….(7)

In Δ TBR,

∠ TBR = 90°           …..[From (1)]

∴ by Pythagoras theorem,

TR² = TB² + BR²       …..(8)

Adding (7) and (8), We get,

TP² + TR² = TA² + AP² + TB² + BR²

TP² + TR² = TA² + BQ² + TB² + AS²      ….[From (2) and (3)]  …(9)

from (6) and (9), we get,

TS² + TQ² = TP² + TR²