Similarity
Class-10-Mathematics-2-Chapter-1-Maharashtra Board
Solutions
Practice set 1.1 (Textbook pages 5 and 6)
Question 1.1.
Base of a triangle is 9 and height is 5. Base of another triangle is 10 and height is 6. Find the ratio of areas of these triangles.
Let the base, height and area of the first triangle be b1, h1 and A1 respectively. Let the base, height and area of the second triangle be b2, h2 and A2 respectively. b1 = 9, h1 = 5, b2 = 10 and h2 = 6. The ratio of areas of two triangles is equal to the ratio of the products of their bases and corresponding heights ∴ \(\frac{A_1}{A_2}=\frac{b_1×h_1}{b_2×h_2}\) ∴ \(\frac{A_1}{A_2}=\frac{9×5}{10×6}\) ∴ \(\frac{A_1}{A_2}=\frac{3}{4}\) ∴ The ratio of the areas of the triangles is 3 : 4.
Question 1.2.
In figure BC ⊥ AB, AD ⊥ AB, BC = 4, AD = 8, then find \(\frac{A(ΔABC)}{A(ΔADB)}\)

BC = 4, AD = 8 ……(Given) ΔABC and ΔADB have same base AB. Areas of triangles with same base are proportional to their corresponding heights. ∴ \(\frac{A(ΔABC)}{A(ΔADB)}=\frac{BC}{AD}\) ∴ \(\frac{A(ΔABC)}{A(ΔADB)}=\frac{4}{8}\) ∴ \(\frac{A(ΔABC)}{A(ΔADB)}=\frac{1}{2}\) ∴ The ratio of the areas of the triangles ΔABC and ΔADB is 1 : 2.
Question 1.3.
In adjoining figure seg PS ⊥ seg RQ seg QT ⊥ seg PR. If RQ = 6, PS = 6 and PR = 12, then find QT.

Solution : RQ = 6, PS = 6 and PR = 12 …….(Given) Area of a triangle = \(\frac{1}{2}\) x base x height ∴ A(ΔPQR) = \(\frac{1}{2}\)x QR x PS ∴ A(ΔPQR) = \(\frac{1}{2}\) x 6 x 6 ∴ A(ΔPQR) = 18 sq units. ……(1) Also, A(ΔPQR) = \(\frac{1}{2}\) x PR x QT ∴ 18 = \(\frac{1}{2}\) x 12 x QT ….[From (1)1 ∴ QT = \(\frac{18}{6}\) ∴ QT = 3 Answer is QT = 3
Question 1.4.
In the given figure, AP ⊥ BC, AD || BC, then find A(ΔABC) : A(ΔBCD).
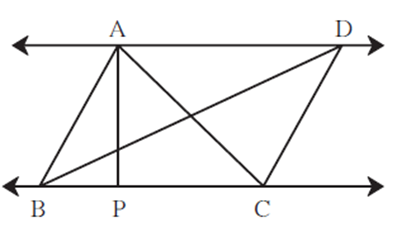
ΔABC and ΔBCD have same base BC. The vertices of ΔABC and ΔBCD lie on the parallel lines AD and BC. The distance between the two parallel lines is the height of the triangles. Distance between parallel lines is constant, ΔABC and ΔBCD have equal heights. Areas of two triangles with same base and equal heights are equal. A(ΔABC) = A(ΔBCD) ∴ \(\frac{A(ΔABC)}{A(ΔBCD)}=\frac{1}{1}\) ∴ A(ΔABC) : A(ΔBCD) = 1:1 Answer is A(ΔABC) : A(ΔBCD) = 1:1.
Question 1.5.
In adjoining figure PQ ⊥ BC, AD ⊥ BC then find following ratios.
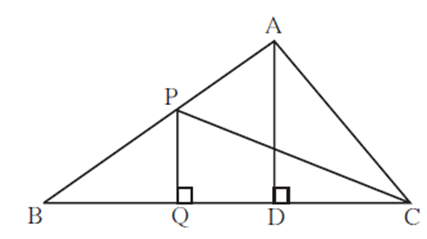
(i)\(\frac{A(ΔPQB)}{A(ΔPBC)}\) (ii) \(\frac{A(ΔPBC)}{A(ΔABC)}\) (iii) \(\frac{A(ΔABC)}{A(ΔADC)}\) (iv) \(\frac{A(ΔADC)}{A(ΔPQC)}\)
(i) ΔPQB and ΔPBC have same height PQ. Areas of triangles with equal heights are proportional to their corresponding bases. \(\frac{A(ΔPQB)}{A(ΔPBC)}=\frac{QB}{BC}\) (ii) ΔPBC and ΔABC have same base BC. Areas of triangles with same base are proportional to their corresponding heights. \(\frac{A(ΔPBC)}{A(ΔABC)}=\frac{PQ}{AD}\) (iii) ΔABC and ΔADC have same height AD. Areas of triangles with same height are proportional to their corresponding bases. \(\frac{A(ΔABC)}{A(ΔADC)}=\frac{BC}{DC}\) (iv) Ratio of areas of two triangles is equal to the ratio of the products of their bases and corresponding heights. \(\frac{A(ΔADC)}{A(ΔPQC)}=\frac{DC×AD}{QC×PQ}\)
Practice set 1.2(Text Book Page 13)
Question 2.1
Given below are some triangles and lengths of line segments. Identify in which figures, ray PM is the bisector of ∠ QPR.
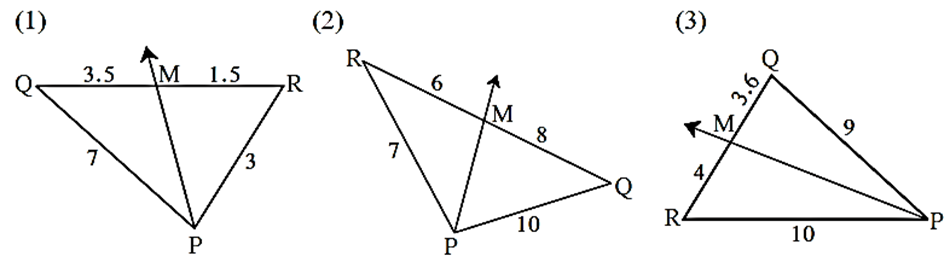
(1) PQ = 7, PR = 3, QM = 3.5 and MR = 1.5 ….(Given) \(\frac{PQ}{PR}=\frac{7}{3}\) ……..(1) \(\frac{QM}{QR}=\frac{3.5}{1.5}=\frac{35}{15}=\frac{7}{3}\) …...(2) In ΔQPR, \(\frac{PQ}{PR}=\frac{QM}{QR}\)……From (1) and (2) ∴ by converse of angle bisector theorem, ∴ ray PM bisects ∠ QPR. (2) PR = 7, PQ = 10, RM = 6 and MQ = 8 ….(Given) \(\frac{PR}{PQ}=\frac{7}{10}\)……..(1) \(\frac{RM}{MQ}=\frac{6}{8}==\frac{3}{4}\) …...(2) ∴ From (1) and (2) \(\frac{PR}{PQ}=\frac{RM}{MQ}\) ∴ ray PM is not bisector of ∠ RPQ. (3) PQ = 9, PR = 10, QM = 3.6 and MR = 4 ….(Given) \(\frac{PQ}{PR}=\frac{9}{10}\) ……..(1) \(\frac{QM}{QR}=\frac{3.6}{4}=\frac{36}{40}=\frac{9}{10}\) …...(2) In ΔQPR, \(\frac{PQ}{PR}=\frac{QM}{QR}\)……From (1) and (2) ∴ by converse of angle bisector theorem, ray PM bisects ∠ QPR.
Question 2.2
In D PQR, PM = 15, PQ = 25, PR = 20, NR = 8. State whether line NM is parallel to side RQ. Give reason.
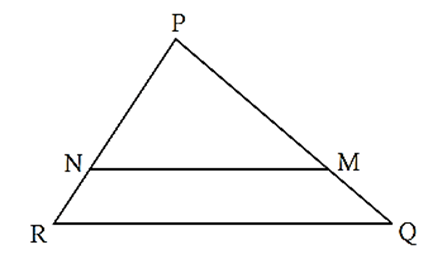
PM = 15, PQ = 25, PR = 20 and NR = 8. PM + MQ = PQ …..(P-M-Q) 15 + MQ = 25 ∴ MQ= 25 - 15, \MQ = 10 PN + NR = PR ….(P-N-R) PN + 8 = 20 PN = 20 - 8, ∴ PN = 12 \(\frac{PN}{NR}=\frac{12}{8}=\frac{3}{2}\)…… (1) \(\frac{PM}{MQ}=\frac{15}{10}=\frac{3}{2}\) …… (2) In ΔPRQ, \(\frac{PN}{NR}=\frac{PM}{MQ}\) …..[From (1) and (2)] ∴ by converse of basic proportionality theorem, line NM || side RQ.
Question 2.3
In ΔMNP, NQ is a bisector of ∠ N. If MN = 5, PN = 7 MQ = 2.5 then find QP .
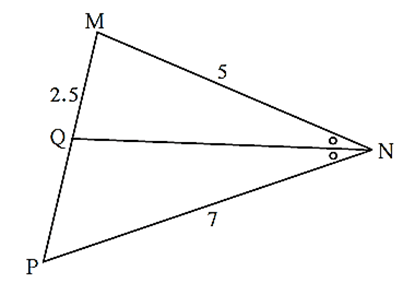
In ΔMNP, ray NQ bisects ∠ MNP ∴ by the theorem of angle bisector of a triangle, \(\frac{MN}{NP}=\frac{MQ}{QP}\) ∴ \(\frac{5}{7}=\frac{2.5}{QP}\) ∴ QP = \(\frac{7×2.5}{5}\) = 3.5. ∴ Answer is QP = 3.5
Question 2.4
Measures of some angles in the figure are given. Prove that \(\frac{AP}{PB}=\frac{AQ}{QC}\)
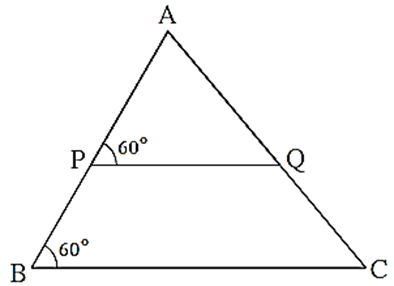
∠ APQ = ∠ ABC = 60° ….(Given) ∴ ∠ APQ ≅ ∠ ABC seg PQ || seg BC ….(Corresponding angles test for parallel lines) (1) In ΔABC, seg PQ ll side BC [From (1)] ∴ \(\frac{AP}{PB}=\frac{AQ}{QC}\) … (Basic proportionality theorem)
Question 2.5
In trapezium ABCD, side AB || side PQ || side DC, AP = 15, PD = 12, QC = 14, find BQ.

Side AB || side PQ || Side DC (Given) ∴ by the property of three parallel lines and their transversals, \(\frac{AP}{PD}=\frac{BQ}{QC}\) ∴ \(\frac{15}{12}=\frac{BQ}{14}\) ∴ BQ x 12 = 15 x 14 ∴ BQ = \(\frac{15×14}{12}=\frac{210}{6}=\frac{35}{2}\) ∴ BQ = 17.5 Answer BQ = 17.5
Question 2.6
Find QP using given information in the figure.
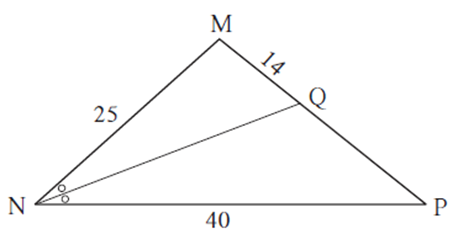
In ΔMNP, ray NQ bisects ∠ MNP ∴ by the theorem of angle bisector of a triangle, \(\frac{MN}{NP}=\frac{MQ}{PQ}\) ∴ \(\frac{25}{40}=\frac{14}{PQ}\) 25 x PQ = 40 x 14 ∴ PQ = \(\frac{40×14}{25}=\frac{8×14}{5}=22.4\) Answer is PQ = 22.4.
Question 2.7
In figure, if AB || CD || FE then find x and AE.

Line AB || line CD || line EF ∴ by the property of three parallel lines and their transversals, \(\frac{BD}{DF}=\frac{AC}{CE}\) ∴ \(\frac{8}{4}=\frac{12}{x}\) ∴ \(8 × x = 4×12\) ∴ \(x=\frac{4×12}{8}\) ∴ x = 6 AE = AC + CE ...(A-C_E) AE = 12 + x AE = 12 + 6 AE = 18 Answer is x = 6 and AE = 18.
Question 2.8
In ΔLMN, ray MT bisects ∠ LMN. If LM = 6, MN = 10, TN = 8, then find LT.

In ΔLMN, ray MT bisects ∠ LMN (Given) ∴ by the theorem of angle bisector of a triangle, \(\frac{LM}{MN}=\frac{LT}{TN}\) ∴ \(\frac{6}{10}=\frac{LT}{8}\) ∴ LT x 10 = 6 x 8 LT = = 4.8 Answer is LT = 4.8.
Question 2.9
In ΔABC, seg BD bisects ∠ ABC.
If AB = x, BC = x + 5, AD = x – 2, DC = x + 2, then find the value of x.
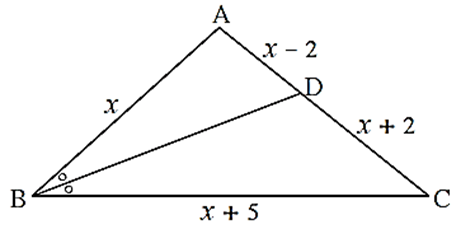
In ΔABC, seg BD bisects ∠ ABC ∴ by the theorem of angle bisector of a triangle, \(\frac{AB}{BC}=\frac{AD}{DC}\) \(\frac{x}{x+5}=\frac{x-2}{x+2}\) ∴ x(x+2) = (x-20)(x+5) ∴ x2 + 2x = x2 + 5x - 2x - 10 ∴ 2x = 3x - 10 ∴ 2x - 3x = -10 ∴ - x = -10 ∴ x = 10 Answer is The value of x is 10.
Question 2.10
In the figure, X is any point in the interior of triangle. Point X is joined to vertices of triangle. Seg PQ || seg DE, seg QR || seg EF. Fill in the blanks to prove that, seg PR || seg DF.
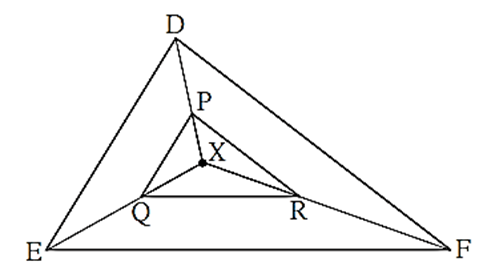
Proof : In ΔXDE, PQ || DE ..........[…..]
∴ \(\frac{XP}{[....]}=\frac{[....]}{QE}\) .......... (I) (Basic proportionality theorem)
In ΔXEF, QR || EF .......... […..]
∴ \(\frac{[...]}{[....]}=\frac{[....]}{[...]}\)..........(II) […..]
∴ \(\frac{[...]}{[....]}=\frac{[....]}{[...]}\) .......... from (I) and (II)
∴ seg PR || seg DF .......... (converse of basic proportionality theorem)
Proof : In ΔXDE, PQ || DE ..........[Given] ∴ \(\frac{XP}{[PD]}=\frac{[XQ]}{QE}\) .......... (I) (Basic proportionality theorem) In ΔXEF, QR || EF .......... [Given] ∴ \(\frac{[XQ]}{[QE]}=\frac{[XR]}{[RF]}\)..........(II) […..] ∴ \(\frac{[XP]}{[PD]}=\frac{[XR]}{[RF]}\) .......... from (I) and (II) ∴ seg PR || seg DF .......... (converse of basic proportionality theorem)
Question 2.11
In ΔABC, ray BD bisects ∠ ABC and ray CE bisects ∠ ACB. If seg AB ≅ seg AC then prove that ED || BC.

In ΔABC, ray BD is the bisector of ∠ ABC ∴ by the theorem of angle bisector of a triangle, \(\frac{AB}{BC}=\frac{AD}{DC}\).………(1) In ΔABC, ray CE is the bisector of ∠ ACB ∴ by the theorem of angle bisector of a triangle, \(\frac{AC}{BC}=\frac{AE}{EB}\)………(2) Seg AB ≅ seg AC …..(Given)….(3) ∴ \(\frac{AC}{BC}=\frac{AC}{BC}\) …..[From (1), (2) and (3)]….(4) In ΔABC, \(\frac{AE}{EB}=\frac{AD}{DC}\)……..[From (1), (2) and (4)] ∴ by converse of basic proportionality theorem, seg ED ll side BC i.e. ED ll BC.
Practice set 1.3(Text Book Page 21)
Question 3.1
In figure, ∠ ABC = 75°, ∠ EDC = 75° state which two triangles are similar and by which test? Also write the similarity of these two triangles by a proper one to one correspondence.
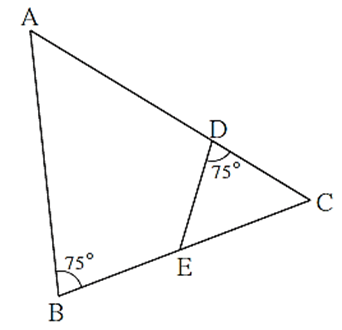
In ΔDCE and ΔBCA, ∠ CDE ≅ ∠ CBA (Each measures 75°) ∠ DCE ≅ ∠ BCA (Common angle) ∴ ∠ DCE ∼ ∠ BCA (AA test of similarity)
Question 3.2
Are the triangles in figure similar? If yes, by which test ?
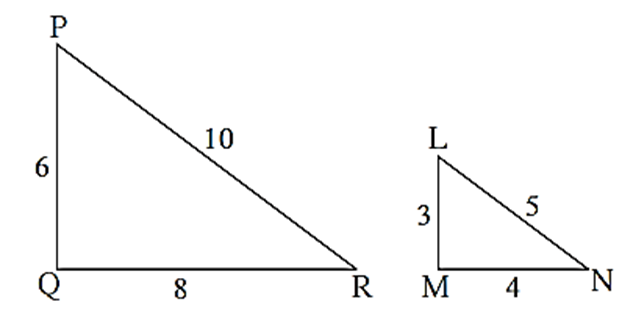
\(\frac{PQ}{LM}=\frac{6}{3}=\frac{2}{1}\) …….(1) \(\frac{QR}{MN}=\frac{8}{4}=\frac{2}{1}\) …..(2) \(\frac{PR}{LN}=\frac{10}{5}=\frac{2}{1}\) …….(3) In ΔPQR and ΔLMN, \(\frac{PQ}{LM}=\frac{QR}{MN}=\frac{PR}{LN}\) ….[From (1), (2) and (3)1 ∴ ΔPQR ∼ ΔLMN (SSS test of similarity)
Question 3.3
As shown in figure, two poles of height 8 m and 4 m are perpendicular to the ground. If the length of shadow of smaller pole due to sunlight is 6 m then how long will be the shadow of the bigger pole at the same time ?
PR and AC are two poles perpendicular to the ground. QR and BC are their shadows respectively. Because the shadows are cast at the same time ∴ ΔPQR ∼ ΔABC \(\frac{PR}{AC}=\frac{QR}{BC}\) …..[Corresponding sides of similar triangles are in proportion] ∴ \(\frac{4}{8}=\frac{6}{x}\) ∴ 4 x x = 8 x 6 ∴ x = \(\frac{8×6}{4} ∴ x = 12, ∴ BC = 12m Answer is -The length of the shadow of the bigger pole will be 12 m.
Question 3.4
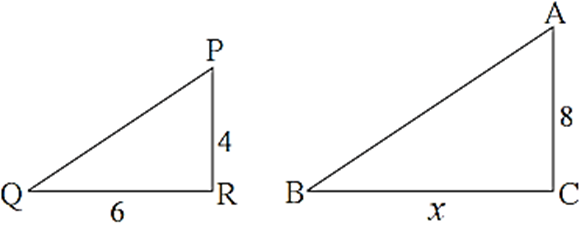
In ΔABC, AP ⊥ BC, BQ ⊥ AC, B-P-C, A-Q-C then prove that, ΔCPA ∼ ΔCQB. If AP = 7, BQ = 8, BC = 12 then find AC.
In ΔCPA and ΔCQB, ∠ CPA ≅ ∠ CQB …(Each measures 90°) ∠ ACP ≅ ∠ BCQ ….(Common angle) ∴ ΔCPA ∼ ΔCQB ….(AA test of similarity) ∴ \(\frac{AP}{BQ}=\frac{AC}{BC}\) ….[Corresponding sides of similar triangles are in proportion] ∴ \(\frac{7}{8}=\frac{AC}{12}\) ∴ AC x 8 = 7 x 12 ∴ AC = 10.5 Answer is AC = 10.5
Question 3.5
Given : In trapezium PQRS, side PQ || side SR, AR = 5AP, AS = 5AQ then prove that, SR = 5PQ
Side PQ ll Side SR and line QS is the transversal ∠ PQS ≅ ∠ RSQ …….(Alternate angles) i.e. ∠ PQA ≅ ∠ RSA ……(Q—A—S)…(1) In ΔPQA and ΔRSA, ∠ PQA ≅ ∠ RSA ….[From (1)] ∠ PAQ ≅ ∠ RAS …..(Vertically opposite angles) ΔPQA ∼ ΔRSA (AA test of similarity) \(\frac{PQ}{RS}=\frac{AQ}{AS}=\frac{AP}{PR}\)….(Corresponding sides of similar triangles are in proportion)..(2) AR = 5AP ....(Given)..(3) Substituting (3) in (2), We get, \(\frac{PQ}{SR}=\frac{AQ}{AS}=\frac{AP}{5AP}\) ∴ \(\frac{PQ}{SR}=\frac{AQ}{AS}=\frac{1}{5}\)…. (4) ∴ \(\frac{PQ}{SR}=\frac{1}{5}\)…[From (4)] ∴ SR = 5PQ
Question 3.6
In trapezium ABCD, (Figure) side AB || side DC, diagonals AC and BD intersect in point O. If AB = 20, DC = 6, OB = 15 then find OD.
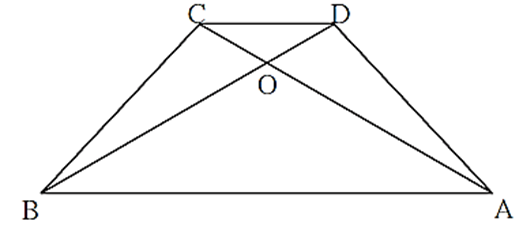
Side AB || side DC and line DB is the transversal, ∠ CDB ≅ ∠ ABD (Alternate angles) i.e. ∠ CDO ≅ ∠ ABO (B—O—D) ….(1) In ΔCOD and ΔAOB, ∠ CDO ≅ ∠ ABO ….[From (1)] ∠ COD ≅ ∠ AOB …..(Vertically opposite angles) ∴ ΔCOD ∼ ΔAOB (AA test of similarity) \(\frac{OD}{OB}=\frac{DC}{AB} …(Corresponding sides of similar triangles are in proportion) ∴ \(\frac{OD}{15}=\frac{6}{20} OD x 20 = 15 x 6 ∴ OD = \(\frac{15×6}{20} = \frac{90}{20}\) ∴ OD = 4.5 Answers is OD = 4.5.
Question 3.7
[] ABCD is a parallelogram point E is on side BC. Line DE intersects ray AB in point T. Prove that DE × BE = CE × TE.

Proof : Seg AB || seg CD …(Opposite sides of parallelogram are parallel) i.e. seg AT || seg CD (A—B—T) Line TD is the transversal, ∴ ∠ ATD ≅ ∠ CDT (Alternate angles) i.e. ∠ BTE ≅ ∠ CDE (A—B—T, T—E—D) ...(1) In ΔBET and ΔCED ∠ BTE ≅ ∠ CDE [From (1)1 ∠ BET ≅ ∠ CED (Vertically opposite angles) ∴ ΔBET ∼ ΔCED (AA test of similarity) ∴ \(\frac{BE}{CE}=\frac{TE}{DE}\) ….(Corresponding sides of similar CE DE triangles are in proportion) ∴ DE × BE = CE × TE.
Question 3.8
In the figure, seg AC and seg BD intersect each other in point P and Prove that, ΔABP ∼ ΔCDP
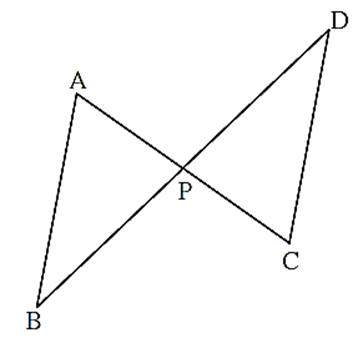
Proof : \(\frac{AP}{CP}=\frac{BP}{DP}\) (Given) ∠ APB ≅ ∠ CPD …..(Vertically opposite angles) ΔABP ∼ ΔCDP (SAS test of similarity)
Question 3.9
In the figure, in ΔABC, point D on side BC is such that, ∠ BAC = ∠ ADC. Prove that, CA2 = CB × CD
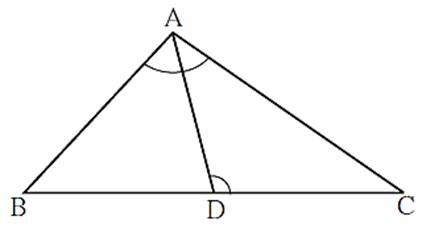
Proof; In ΔBAC and ΔADC, ∠ BAC ≅ ∠ ADC ….(Given) ∠ ACB ≅ ∠ DCA …..(Common angle) ΔBAC ∼ ΔADC ….(AA test of similarity) ∴ \(\frac{CA}{CD}=\frac{CB}{CA}\) …….(Corresponding sides of similar triangles are in proportion) ∴ CA2 = CB × CD.
Practice set 1.4(Text Book Page 25)
Question 4.1
The ratio of corresponding sides of similar triangles is 3 : 5; then find the ratio of their areas.
Let the corresponding sides of two similar triangles be x1 and x2. Let their respective areas be A1 and A2. x1 : x2 = 3 : 5 ….(Given) \(\frac{x_1}{x_2}=\frac{3}{5}\) …(1) The two triangles are similar. ∴ \(\frac{A_1}{A_2}=\frac{{x_1}^2}{{x_2}^2}\) ……(Theorem of areas of similar triangles) ∴ \(\frac{A_1}{A_2}=(\frac{x_1}{x_2})^2 =(\frac{3}{5})^2\) …[From (1)] \(\frac{A_1}{A_2}=\frac{9}{25}\) A1 : A2 = 9 : 25 Answer is - The ratio of the areas of two similar triangles is 9 : 25.
Question 4.2
If ΔABC ∼ ΔPQR and AB: PQ = 2:3, then fill in the blanks.
\(\frac{A(ΔABC)}{A(ΔPQR)}=\frac{AB^2}{[...]}=\frac{2^2}{3^2}=\frac{[...]}{[...]}\)
\(\frac{A(ΔABC)}{A(ΔPQR)}=\frac{AB^2}{[PQ^2]}=\frac{2^2}{3^2}=\frac{[4]}{[9]}\)
Question 4.3
If ΔABC ∼ ΔPQR, A (ΔABC) = 80, A (ΔPQR) = 125, then fill in the blanks.
\(\frac{A(ΔABC)}{A(Δ....)}=\frac{80}{125}\)
∴ \(\frac{AB}{PQ}=\frac{[...]}{[...]}\)
\(\frac{A(ΔABC)}{A(ΔPQR)}=\frac{80}{125}\) ∴ \(\frac{AB}{PQ}=\frac{[4]}{[5]}\) Explanation : ΔABC ∼ ΔPQR. By the theorem of areas of similar triangles \(\frac{A(ΔABC)}{A(ΔPQR)}=\frac{AB^2}{PQ^2}=\frac{80}{125}=\frac{16}{25}\) ∴ \(\frac{AB}{PQ}=\frac{[4]}{[5]}\)
Question 4.4
ΔLMN ∼ ΔPQR, 9 x A(ΔPQR ) = 16 x A(ΔLMN). If QR = 20 then find MN.
ΔLMN ∼ ΔPQR ....(Given) 9 x A(ΔPQR) = 16 x A(ΔLMN) ∴ \(\frac{A(ΔLMN)}{A(ΔPQR)}=\frac{9}{16}\) … (1) Now \(\frac{A(ΔLMN)}{A(ΔPQR)}=\frac{MN^2}{QR^2}\) ….(Theorem of areas of similar triangles) ∴ \( \frac{9}{16}=\frac{MN^2}{QR^2}\)…..from (1) ∴ \(\frac{MN}{QR}=\frac{3}{4}\) ∴ \(MN=\frac{20×3}{4}=15\) ….(…QR=20 given) Answer is –MN=15
Question 4.5
Areas of two similar triangles are 225 sq.cm. 81 sq.cm. If a side of the smaller triangle is 12 cm, then find corresponding side of the bigger triangle.
Let the areas of two similar triangles be A1 and A2. Let their respective corresponding sides be s1 and s2. A1 = 225 sq cm, A2 = 81 sq cm and s2 = 12 cm. …(Given) The two triangles are similar ∴ by the theorem of areas of similar triangles, \(\frac{A_1}{A_2}=\frac{{s_1}^2}{{s_2}^2}\) ∴ \(\frac{225}{81}=\frac{{s_1}^2}{12^2}\) ∴ \({s_1}^2=\frac{225×12^2}{81}\) ∴ \(s_1=\frac{15×12}{9}\) …(Taking square roots on both the sides) ∴ s1 = 20 cm Answer is-The corresponding side of the bigger triangle is 20 cm.
Question 4.6
ΔABC and ΔDEF are equilateral triangles. If A(ΔABC) : A (ΔDEF) = 1 : 2 and AB = 4, find DE.
ΔABC and ΔDEF are equilateral triangles. ∠ A = ∠ B = ∠ C = ∠ D = ∠ E = ∠ F = 60° …(Angles of equilateral triangle) In ΔABC and ΔDEF, ∠ A ≅ ∠ D and ∠ B ≅ ∠ E ….(Each measures 60°) ∴ ΔABC ∼ ΔDEF ….(AA test of similarity) By theorem of areas of similar triangles, \(\frac{A(ΔABC)}{A(ΔDEF)}=\frac{AB^2}{DE^2}\) .....(1) A(ΔABC) : A(ΔDEF) = 1 : 2 and AB = 4 ….(Given) .....(2) ∴ \(\frac{1}{2}=\frac{4^2}{DE^2}\) ….[From (1) and (2)] ∴ DE2 = 42 x 2 ∴ DE = 4\(\sqrt{2}\) ….(Taking square roots of both the sides) Answer is DE = 4\(\sqrt{2}\)
Question 4.7
In figure seg PQ || seg DE, A(ΔPQF) = 20 units, PF = 2 DP, then find A([] DPQE) by completing the following activity.

A(ΔPQF) = 20 sq units, PF = 2 DP, Let us assume DP = x. ∴ PF = 2x
DF = DP + [...] = [...] + [...] = 3x
In Δ FDE and Δ FPQ,
∠ FDE ≅ ∠ [...] .......... corresponding angles
∠ FED ≅ ∠ [...] .......... corresponding angles
∴ ΔFDE ∼ ΔFPQ .......... AA test
∴\(\frac{A(ΔFDE)}{A(ΔFPQ)}= \frac{[...]}{[...]}=\frac{(2x)^2}{(2x)^2}=\frac{9}{4}\)
A(ΔFDE) = \(frac{9}{4}\) A(ΔFPQ ) = \(frac{9}{4}\) x [...] = [ ..... ]
A([] DPQE) = A(ΔFDE) − A(ΔFPQ)
= [ ... ] – [... ]
= [ .... ]
A(ΔPQF) = 20 sq units, PF = 2 DP, Let us assume DP = x. ∴ PF = 2x DF = DP + [PF ] = [ x ] + [ 2x ] = 3x In Δ FDE and Δ FPQ, ∠ FDE ≅ ∠ [ FPQ ] .......... corresponding angles ∠ FED ≅ ∠ [FQP ] .......... corresponding angles ∴ ΔFDE ~ ΔFPQ .......... AA test ∴\(\frac{A(ΔFDE)}{A(ΔFPQ)}= \frac{[DF^2]}{[PF^2]}=\frac{(2x)^2}{(2x)^2}=\frac{9}{4}\) A(ΔFDE) = \(frac{9}{4}\) A(ΔFPQ ) = \(frac{9}{4}\) x [20] = [ 45 sq units ] A([] DPQE) = A(ΔFDE) − A(ΔFPQ) = [ 45 ] – [ 20 ] = [ 25 sq units ]
PDF-Notes,Solution,Text Book
Main Page : – Maharashtra Board Class 10th-Mathematics – All chapters notes, solutions, videos, test, pdf.
Next Chapter : Chapter-2-Pythagoras Theorem – Online Notes
We reply to valid query.