Solutions-Part-2-Class-10-Mathematics-1-Chapter-1-Linear Equations in Two Variables-Maharashtra Board

\(\begin{vmatrix} 3 &2 \\ 4& 5 \end{vmatrix}\) = 3 ×  [ 5] − [2 ] × 4 = [15 ] − 8 = [ 7]

\(\begin{vmatrix} -1 &7 \\ 2& 4 \end{vmatrix}\) = (−1) × 4 − 7 × 2 = − 4 − 14 = −18

Answer is −18

\(\begin{vmatrix} 5 &3 \\ -7& 0 \end{vmatrix}\) = 5 × 0 − 3 × (−7) = 0 + 21 = 21

Answer is 21

  \(\begin{vmatrix} \frac{7}{3} &\frac{5}{3} \\ \frac{3}{2}& \frac{1}{2} \end{vmatrix}\)

= \(\frac{7}{3}\times \frac{1}{2}-\frac{5}{3}\times \frac{3}{2}\)=\(\frac{7}{6}-\frac{15}{6}=\frac{7-15}{6}\)

= \(-\frac{4}{3}\)

Answer is\(-\frac{4}{3}\)

3x − 4y = 10

4x + 3y = 5

In above given equations

 a₁ = 3, b₁ = − 4, c₁ = 10

 a₂ = 4, b₂ = 3, c₂ = 5

D = \(\begin{vmatrix} a_1 &b_1 \\ a_2& b_2 \end{vmatrix}\)  = \(\begin{vmatrix} 3 &-4 \\ 4& 3 \end{vmatrix}\)

= 3 × 3 −(− 4) × 4 = 9 + 16 = 25

D_x = \(\begin{vmatrix} c_1 &b_1 \\ c_2& b_2 \end{vmatrix}\)   = \(\begin{vmatrix} 10 &-4 \\ 5& 3 \end{vmatrix}\)

= 10 × 3 −(− 4) × 5 = 30 + 20 = 50

D_y = \(\begin{vmatrix} a_1 &c_1 \\ a_2& c_2 \end{vmatrix}\) = \(\begin{vmatrix} 3 &10 \\ 4& 5 \end{vmatrix}\)

= 3 × 5 − 10 × 4  = 15 − 40 = − 25

By Cramers’s rule,

\(x=\frac{D_x}{D} = \frac{50}{25}=2\)

and \(y=\frac{D_y}{D}= \frac{-25}{25}=-1\)

Answer is (x, y) = (2, − 1)

Writing the equation in ax + by = c form

 4x + 3y = 4

 6x + 5y = 8

In above given equations

 a₁ = 4, b₁ = 3, c₁ = 4

 a₂ = 6, b₂ = 5, c₂ = 8

D = \(\begin{vmatrix} a_1 &b_1 \\ a_2& b_2 \end{vmatrix}\)  = \(\begin{vmatrix} 4 &3 \\ 6& 5 \end{vmatrix}\)  

= 4 × 5 − 3 × 6 = 20 −18 = 2

D_x = \(\begin{vmatrix} c_1 &b_1 \\ c_2& b_2 \end{vmatrix}\)  =\(\begin{vmatrix} 4 &3 \\ 6& 5 \end{vmatrix}\)  

= 4 × 5 − 3 × 8  = 20 - 24 = − 4

D_y = \(\begin{vmatrix} a_1 &c_1 \\ a_2& c_2 \end{vmatrix}\)  = \(\begin{vmatrix} 4 &3 \\ 6& 5 \end{vmatrix}\)

= 4 × 8 − 4 × 6  = 32 − 24 = 8

By Cramers’s rule,

\(x=\frac{D_x}{D} = \frac{-4}{2}=-2\)

and \(y=\frac{D_y}{D}= \frac{8}{2}=4\)

Answer is (x, y) = (− 2, 4)

x + 2y = − 1

2x − 3y = 12    

In above given equations

 a₁ = 1, b₁ = 2, c₁ = −1

 a₂ = 2, b₂ = −3, c₂ = 12

D = \(\begin{vmatrix} a_1 &b_1 \\ a_2& b_2 \end{vmatrix}\)  = \(\begin{vmatrix} 1 &2 \\ 2& -3 \end{vmatrix}\)

= 1 × (− 3) − 2× 2 = −3 − 4 = −7

D_x = \(\begin{vmatrix} c_1 &b_1 \\ c_2& b_2 \end{vmatrix}\) = \(\begin{vmatrix} -1 &2 \\ 12& -3 \end{vmatrix}\)

= −1 × (− 3) − 2× 12 =  3 − 24 = −21

D_y = \(\begin{vmatrix} a_1 &c_1 \\ a_2& c_2 \end{vmatrix}\) = \(\begin{vmatrix} 1 &-1 \\ 2& 12 \end{vmatrix}\)

= 1 × 12 − 2 × −1 = 12 +2 = 14

By Cramers’s rule,

\(x=\frac{D_x}{D} = \frac{-21}{-7}=3\)

and \(y=\frac{D_y}{D}= \frac{14}{-7}=-2\)

Answer is (x, y) = (3, −2)

6x − 4y = −12

8x − 3y = −2

In above given equations

 a₁ = 6, b₁ = −4, c₁ = −12

 a₂ = 8, b₂ = −3, c₂ = −2

D = \(\begin{vmatrix} a_1 &b_1 \\ a_2& b_2 \end{vmatrix}\)  = \(\begin{vmatrix} 6 &-4 \\ 8& -3 \end{vmatrix}\)

= 6 × (− 3) − (−4) × 8  = −18 + 32 = 14

D_x = \(\begin{vmatrix} c_1 &b_1 \\ c_2& b_2 \end{vmatrix}\)  = \(\begin{vmatrix} -12 &-4 \\ -2& -3 \end{vmatrix}\)

= (− 12) × (− 3) − (−4) × (− 2) = 36 − 8 = 28

D_y = \(\begin{vmatrix} a_1 &c_1 \\ a_2& c_2 \end{vmatrix}\) = \(\begin{vmatrix} 6 &-12 \\ 8& -2 \end{vmatrix}\)

= 6 × (− 2) − (−12) × 8  = −12 + 96 = 84

By Cramers’s rule,

\(x=\frac{D_x}{D} = \frac{28}{14}=2\)

and \(y=\frac{D_y}{D}= \frac{84}{14}=6\)

Answer is (x, y) = (2, 6)

4m + 6n = 54

3m + 2n = 28

In above given equations

 a₁ = 4, b₁ = 6, c₁ = 54

 a₂ = 3, b₂ = 2, c₂ = 28

D = \(\begin{vmatrix} a_1 &b_1 \\ a_2& b_2 \end{vmatrix}\)  = \(\begin{vmatrix} 4 &6 \\ 3& 2 \end{vmatrix}\)

= 4 × 2 − 6 × 3  =  8 − 18 = − 10

D_m = \(\begin{vmatrix} c_1 &b_1 \\ c_2& b_2 \end{vmatrix}\)  = \(\begin{vmatrix} 54 &6 \\ 28& 2 \end{vmatrix}\)

= 54 × 2 − 6 × 28 = 108 − 168 = −60

D_n = \(\begin{vmatrix} a_1 &c_1 \\ a_2& c_2 \end{vmatrix}\)  = \(\begin{vmatrix} 4 &54 \\ 3& 28 \end{vmatrix}\)

= 4 × 2 8 − 54 × 3  = 112 −162 = −50

By Cramers’s rule,

\(x=\frac{D_m}{D} = \frac{-60}{-10}=6\)

and \(y=\frac{D_n}{D}= \frac{-50}{-10}=5\)

Answer is (m, n) = (6, 5)

2x + 3y = 2

 x – \(\frac{y}{2}=\frac{1}{2}\)

In above given equations

 a₁ = 2, b₁ = 3, c₁ = 2

 a₂ = 1, b₂ = \(-\frac{1}{2}\)  , c₂ = \(\frac{1}{2}\)

D = \(\begin{vmatrix} a_1 &b_1 \\ a_2& b_2 \end{vmatrix}\)  = \(\begin{vmatrix} 2 &3 \\ 1& -\frac{1}{2} \end{vmatrix}\)

= 2 × (\(-\frac{1}{2}|)) − 3 × 1  = –1 – 3 = –4

D_x = \(\begin{vmatrix} c_1 &b_1 \\ c_2& b_2 \end{vmatrix}\) = \(\begin{vmatrix} 2 &3 \\ \frac{1}{2}& -\frac{1}{2} \end{vmatrix}\)

= 2 × (\(-\frac{1}{2}\)) − 3 × \(\frac{1}{2}\)  = −1− \(\frac{3}{2}\) = − \(\frac{5}{2}\)

D_y = \(\begin{vmatrix} a_1 &c_1 \\ a_2& c_2 \end{vmatrix}\)  = \(\begin{vmatrix} 2 &2 \\ 1& \frac{1}{2} \end{vmatrix}\)

= 2 × (\(\frac{1}{2}\)) − 2 × 1 =  1 − 2 = −1

By Cramers’s rule,

\(x=\frac{D_x}{D} = \frac{-\frac{5}{2}}{-4}=\frac{5}{8}\)

and \(y=\frac{D_y}{D}= \frac{-1}{-4}=\frac{1}{4}\)

Answer is (x, y) = (\(\frac{5}{8}\), \(\frac{1}{4}\))

\(\frac{2}{x}-\frac{3}{y}\) = 15  …….. (1)

\(\frac{8}{x}+\frac{5}{y}\) = 77 …….. (2)

Substituting a for  \(\frac{1}{x}\)  and b for \(\frac{1}{y}\)  the given equations become,

2a − 3b = 15  …….(3)

8a + 5b = 77  ……(4)

Multiplying equation (3) by 4,

8a − 12b = 60  ……(5)

Subtracting equation (5) from equation (4),

\(\begin{array}{rrrrrrr}
& 8a & + & 5b & = & 77 &\text{…..(4)}\\
- & & & & & & \\
&8a & - & 12b & = & 60 &\text{…..(5)} \\
-& & +& & &-& \\ \hline
&  &  & 17b & = & 17 & \\
\end{array}\)

∴ b = 1

Substituting b = 1 in equation (3),

2a −3(1) = 15,  ∴ 2a – 3 = 15, ∴ 2a = 15 + 3

2a = 18,  ∴ a=9

Resubstituting the values of a and b,

a  = \(\frac{1}{x}\)  = 9 and b =  \(\frac{1}{y}\)  = 1

∴ x =  \(\frac{1}{9}\)  , and y = 1

Answer is (x, y) = ( \(\frac{1}{9}\), 1)

  \(\frac{10}{x+y}+\frac{2}{x-y}\) = 4  …….. (1)

\(\frac{15}{x-y}-\frac{5}{x-y}\) = –2  …….. (2)

Substituting a for  \(\frac{1}{x+y}\)  and b for \(\frac{1}{x-y}\)  the given equations become,

10a + 2b = 4  …….(3)

15a – 5b = –2  ……(4)

Multiplying equation (3) by 5,

50a + 10b = 20  ……(5)

Multiplying equation (4) by 2,

30a – 10b = –4  ……(6)

Adding equation (5) and (6),

\(\begin{array}{rrrrrrr}
& 50a & + & 10b & = & 20 &\text{…..(5)}\\
+ & & & & & & \\
&30a & - & 10b & = & -4 &\text{…..(6)} \\
& & & & && \\ \hline
&80a  &  &  & = & 16 & \\
\end{array}\)

   ∴ a = \(\frac{16}{80}\) = \(\frac{1}{5}\)

Substituting a = \(\frac{1}{5}\) in equation (3),

\(10(\frac{1}{5})\) + 2b = 4,  ∴ 2 + 2b  = 4, ∴ 2b = 4 – 2 = 2

∴ b = 1

Resubstituting the values of a and b,

a  =  \(\frac{1}{x+y}=\frac{1}{5}\)    and b = \(\frac{1}{x-y}\) = 1

∴ x + y = 5 ….(7)  , and x — y = 1 …..(8)

Adding equation (5) and (6),

\(\begin{array}{rrrrrrr}
& x & + & y & = & 5 &\text{…..(7)}\\
+ & & & & & & \\
&x & - & y & = & 1 &\text{…..(8)} \\
& & & & && \\ \hline
&2x  &  &  & = & 6 & \\
\end{array}\)

∴ x = 6/2 = 3

Substituting x = 3 in equ. (7),

3 + y = 5, ∴ y = 5 – 3 = 2

 Answer is (x, y) = (3, 2 )

\(\frac{27}{x-2}+\frac{31}{y+3}\) = 85 …….. (1)

\(\frac{31}{x-2}-\frac{27}{y+3}\) = 89  …….. (2)

Substituting a for \(\frac{1}{x-2}\) and b for  \(\frac{1}{y+3}\) the given equations become,

27a  +  31b = 85  …….(3)

31a – 27b = 89  ……(4)

Adding equation (3) and (4),

\(\begin{array}{rrrrrrr}
& 27a & + & 31b & = & 85 &\text{…..(3)}\\
+ & & & & & & \\
&31a & - & 27b & = & 89 &\text{…..(4)} \\
& & & & && \\ \hline
&58a  &+  &58b  & = & 174 & \\
\end{array}\)

  ∴  a + b = 3 (Dividing both sides by 58)….. (5)

 Subtracting equation (3) from equation (4),

\(\begin{array}{rrrrrrr}
& 31a & - & 27b & = & 89 &\text{…..(3)}\\
- & & & & & & \\
&27a & + & 31b & = & 85 &\text{…..(4)} \\
&- &- & & &-& \\ \hline
&4a  &-  &4b  & = & 4 & \\
\end{array}\)

   ∴ a - b = 1 (Dividing both sides by 4) … (6)

 Adding equation (5) and (6),

\(\begin{array}{rrrrrrr}
& a & + & b & = & 3 &\text{…..(5)}\\
+ & & & & & & \\
&a & - & b & = & 1 &\text{…..(6)} \\
& & & & && \\ \hline
&2a  &  &  & = & 4 & \\
\end{array}\)

∴ a = 2

 Substituting a = 2  in equation (5),

2 + b = 3,  ∴ b  = 3 – 2 , ∴ b = 1

Resubstituting the values of a and b,

a  = \(\frac{1}{x-2}\) = 2   

∴ 2(x – 2) = 1, ∴ 2x – 4 = 1,  ∴ 2x = 1+ 4 =5 ∴x = 5/2

 b = \(\frac{1}{y+3}\)  = 1

∴ y + 3 = 1, ∴ y = 1 – 3 = –2 , ∴ y = – 2

Answer is (x, y) = ( 5/2, – 2)

\(\frac{1}{3x+y}+\frac{1}{3x-y}\) = \(\frac{3}{4}\) …….. (1)

\(\frac{1}{2(3x+y)}-\frac{1}{2(3x-y}\) = \(-\frac{1}{8}\)  …….. (2)

Substituting a for \(\frac{1}{3x+y}\)   and b for \(\frac{1}{3x-y}\) the given equations become,

a  +  b = \(\frac{3}{4}\)   …….(3)

\(\frac{a}{2}-\frac{b}{2}\)  = \(-\frac{1}{8}\)  ……(4)

Multiplying equation (3) by 4

4a + 4b = 3 …….(5)

Multiplying equation (4) by 8

4a – 4b = – 1 …….(6)

Adding equation (5) and (6),

\(\begin{array}{rrrrrrr}
& 4a & + & 3b & = & 3 &\text{…..(3)}\\
+ & & & & & & \\
&4a & - & 4b & = & -1 &\text{…..(4)} \\
& & & & && \\ \hline
&8a  &  &  & = & 2 & \\
\end{array}\)

∴ a  = \(\frac{1}{4}\)

Substituting  a  =\(\frac{1}{4}\) in equation (5)

4(¼) + 4b = 3, ∴ 1 + 4b = 3, ∴ 4b = 3 – 1 = 2

∴b = \(\frac{1}{2}\)

Resubstituting the values of a and b,

a  = \(\frac{1}{3x+y}\) = \(\frac{1}{4}\) 

∴ 3x + y = 4  …..(7)

And  

 b = \(\frac{1}{3x-y}\) =\(\frac{1}{2}\)

∴ 3x – y  = 2 …….(8)

Adding equation (7) and (8),

\(\begin{array}{rrrrrrr}
& 3x & + & y & = & 4 &\text{…..(7)}\\
+ & & & & & & \\
&3x & - & y & = & 2 &\text{…..(8)} \\
& & & & && \\ \hline
&6x  &  &  & = & 6 & \\
\end{array}\)

∴ x  = 1

Substituting x =1 in equation 7

∴ 3 + y = 4 ∴ y = 4 – 3 = 1

Answer is (x, y) = (1, 1 )

Let the greater number be x and the smaller number be y.

From the first condition,

x – y = 3  …..(1)

Thrice the greater number = 3x.

Twice the smaller number = 2y.

From the second condition,

3x + 2y = 19

Multiplying equation (1) by 2,

2x – 2y = 6  …..(3)

Adding equations (2) and (3),

\(\begin{array}{rrrrrrr}
& 3x & + & 2y & = & 19 &\text{…..(2)}\\
+ & & & & & & \\
&2x & - & 2y & = & 6 &\text{…..(3)} \\
& & & & && \\ \hline
&5x  &  &  & = & 25 & \\
\end{array}\)

∴ x = 5

Substituting x = 5 in equation (1),

5 – y = 3 – y = 3 – 5  –y = –2  ∴ y = 2

The required numbers are 5 and 2 is the answer.

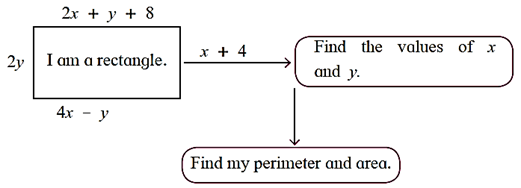
The opposite sides of a rectangle are of equal lengths.

 2x + y + 8 = 4x – y

∴ 2x – 4x + y + y = – 8

∴ – 2x + 2y = – 8

∴ – x + y = – 4  (Dividing both the sides by 2)  …..(1)

Also, x + 4 = 2y

∴ x – 2y = – 4 ……..(2)

Adding equations (1) and (2),

\(\begin{array}{rrrrrrr}
& -x & + & y & = & -4 &\text{…..(1)}\\
+ & & & & & & \\
&x & - & 2y & = & -4 &\text{…..(2)} \\
& & & & && \\ \hline
&  &  &  -y& = & -8 & \\
\end{array}\)

∴ y = 8

Substituting y = 8 in equation (2),

x – 2(8) = – 4,  ∴ x –16 = – 4 , ∴ x = – 4 + 16 = 12

∴ x  = 12

The length of the rectangle = 4x – y = 4(12) – 8 = 48 – 8 = 40

The breadth of the rectangle = 2y = 2 × 8 = 16

The area of a rectangle = l × b

= 40 × 16 = 640 sq. units

The perimeter of the rectangle = 2(l + b)

= 2(40 + 16)

= 2 × 56= 112 units

Answer is x = 12; y = 8. The area of the rectangle is 640 sq. units and its perimeter is 112 units.

Let the father’s present age be x years and the son’s present age be y years.

From the first condition,

x + 2y = 70  …… (1)

Double the age of father = 2x.

From the second condition,

2x + y = 95  …..(2)

Multiplying equation (1) by 2,

2x + 4y = 140  ……(3)

Subtracting equation (2) from equation (3),

\(\begin{array}{rrrrrrr}
& 2x &+ & 4y & = & 140 &\text{…..(3)}\\
- & & & & & & \\
& 2x & + & y & = & 95 &\text{…..(2)} \\
-& &- & & &-& \\ \hline
&  &  &  3y& = & 45 & \\
\end{array}\)

∴ y = 15

Substituting y = 15 in equation (1),

x + 2(15) = 70,  ∴ x + 30 = 70

∴ x = 70 – 30 , ∴ x = 40

Answer is the father’s present age is 40 years and the son’s present age is 15 years.

Let the numerator of the fraction be x and its denominator be y.

Twice the numerator = 2x.

From the first condition,

y = 2x + 4, ∴ 2x + 4 = y,  ∴ 2x  – y = – 4 ...(1)

If 6 is subtracted both from the numerator and the denominator, then the numerator becomes (x – 6) and the denominator becomes ( y – 6).

From the second condition,

y – 6 = 12(x – 6)

∴ y – 6 = 12x – 72

 12x – 72 = y – 6

 12x – y = - 6 + 72

 12x – y = 66  ……(2)

Subtracting equation (1) from equation (2),

\(\begin{array}{rrrrrrr}
& 12x & - & y & = & 66 &\text{…..(2)}\\
- & & & & & & \\
& 2x & - & y & = & -4 &\text{…..(1)} \\
-& &+ & & &+ & \\ \hline
& 10x &  &  & = & 70 & \\
\end{array}\)

∴ x = 7

Substituting x = 7 in equation (1),

2(7) – y = – 4

 14 – y = – 4

– y = – 4 – 14

– y = –18,  ∴ y = 18

The numerator, x is 7 and the denominator, y is 18

Answer is- The required fraction is \(\frac{7}{18}\)

Let the weight of a box of type A be x ton and that of a box of type B be y ton.

The weight of 150 boxes of type A = 150x ton.

The weight of 100 boxes of type B = 100 y ton.

From the first condition,

150x + 100y = 10

 15x + 10y = 1  (Dividing both the sides by 10) …… (1)

Similarly, from the second condition,

260x + 40y = 10

 26x + 4y = 1  (Dividing both the sides by 10) …… (2)

Multiplying equation (1) by 2 and equation (2) by 5,

30x + 20y = 2  ….(3)

130x + 20y = 5  ……(4)

Subtracting equation (3) from equation (4),

\(\begin{array}{rrrrrrr}
& 130x & + & 20y & = & 5 &\text{…..(4)}\\
- & & & & & & \\
& 30x & + & 20y & = & 2 &\text{…..(3)} \\
-& &- & & &- & \\ \hline
& 100x &  &  & = & 3 & \\
\end{array}\)

∴ x = \(\frac{3}{100}\)

Substituting x = \(\frac{3}{100}\)  in equation (1),

15(\(\frac{3}{100}\)) + 10y = 1

\(\frac{45}{100}\) + 10y = 1

10y = 1- \(\frac{45}{100}\)

∴ 10y = \(\frac{55}{100}\) =

∴ y = \(\frac{45}{1000}\)  ...(Dividing both the sides by 10)

Answer is - The weight of a box of type A is \(\frac{3}{100}\) ton

 i.e.  ton = \(\frac{3}{100}\) × 1000 kg = 30 kg and

the weight of a box of type B is \(\frac{55}{1000}\)  ton

i.e.  ton = \(\frac{55}{1000}\) × 1000 kg = 55kg

Let Vishal travelled x km by bus and y km by plane.

Time = (distance)/(speed)

Time taken by Vishal while travelling by bus

= \(\frac{x}{60}\)h

Time taken by Vishal while travelling by plane

= \(\frac{y}{700}\)h

From the given conditions,

x + y = 1900   ……(1)

and \(\frac{x}{60}+\frac{y}{700}\) = 5 ….(2)

Multiplying equation (2) by 2100, the LCM of 60 and 700, 

\(\frac{x}{60}×2100+\frac{y}{700}×2100\) = 5 × 2100

∴ 35x + 3y = 10500  …….(3)

Multiplying equation (1) by 3,

3x + 3y = 5700  …..(4)

Subtracting equation (4) from equation (3),

\(\begin{array}{rrrrrrr}
& 35x & + & 3y & = & 10500 &\text{…..(3)}\\
- & & & & & & \\
& 3x & + & 3y & = & 5700 &\text{…..(4)} \\
-& &- & & &- & \\ \hline
& 32x &  &  & = & 4800 & \\
\end{array}\)

∴ x =  \(\frac{4800}{32}\) = 150

∴ x = 150

Answer is- Vishal travelled 150 km by bus.