Motion in a Plane
Maharashtra Board-Class-11-Science-Physics-Chapter-3
Solutions
Question 1.
Choose the correct option.
(i) An object thrown from a moving bus is on example of
(A) Uniform circular motion
(B) Rectilinear motion
(C) Projectile motion
(D) Motion in one dimension
(C) Projectile motion
(ii) For a particle having a uniform circular motion, which of the following is constant
(A) Speed
(B) Acceleration
(C) Velocity
(D) Displacement
(A) Speed
(iii) The bob of a conical pendulum under goes
(A) Rectilinear motion in horizontal plane
(B) Uniform motion in a horizontal circle
(C) Uniform motion in a vertical circle
(D) Rectilinear motion in vertical circle
(B) Uniform motion in a horizontal circle
(iv) For uniform acceleration in rectilinear motion which of the following is not correct?
(A) Velocity-time graph is linear
(B) Acceleration is the slope of velocity time graph
(C) The area under the velocity-time graph equals displacement
(D) Velocity-time graph is nonlinear
(D) Velocity-time graph is nonlinear
(v) If three particles A, B and C are having velocities \(\vec{V_A}\), \(\vec{V_B}\) and \(\vec{V_C}\) which of the following formula gives the relative velocity of A with respect to B
(A) \(\vec{V_A}\) + \(\vec{V_B}\)
(B ) \(\vec{V_A}\) − \(\vec{V_C}\) + \(\vec{V_B}\)
(C) \(\vec{V_A}\) − \(\vec{V_B}\)
(D) \(\vec{V_C}\) − \(\vec{V_A}\)
(C) \(\vec{V_A}\) − \(\vec{V_B}\)
Question 2.
Answer the following questions.
(i) Separate the following in groups of scalar and vectors: velocity, speed, displacement, work done, force, power, energy, acceleration, electric charge, angular velocity.
Scalars : speed, work done, power, energy, electric charge.
Vectors : velocity, displacement, force, acceleration, angular velocity.
(ii) Define average velocity and instantaneous velocity. When are they same?
Average velocity : The average velocity of a particle is the displacement of the particle divided by the time elapsed during which the displacement occurs.
If \(\vec{x_1}\) and \(\vec{x_2}\) are the position vectors of the particle at instants t1 and t2 respectively, then
\(\vec{v_{av}}=\frac{displacement}{elapsed\,time} = \frac{Δ\vec{x}}{Δt}\) = \(\frac{\vec{x_2}-\vec{x_1}}{t_2-t_1}\)
Instantaneous velocity : The velocity at a given instant is called the instantaneous velocity and is defined as the limiting value of the average velocity as the time interval approaches zero.
\(\vec{v}=\lim\limits_{Δt\to{0}}\frac{Δ\vec{x}}{Δt}= \frac{d\vec{x}}{dt}\)
When a particle moves with uniform velocity (i.e., a velocity which remains constant with time both in magnitude and direction), the acceleration is zero and the average velocity equals the instantaneous velocity.
(iii) Define free fall.
When a body starts with zero velocity at a certain height from the ground and falls under the influence of the gravity of the Earth, ignoring air resistance and buoyancy of air, it is said to be in free fall..
(iv) If the motion of an object is described by x = f(t) write formulae for instantaneous velocity and acceleration.
Given x =f(t), the instantaneous velocity is
\(v=\frac{dx}{dt}=\frac{d}{dt}f(t)\)
and the instantaneous acceleration is
\(a=\frac{dv}{dt}=\frac{d^2x}{dt^2}=\frac{d^2}{dt^2}f(t)\)
(v) Derive equations of motion for a particle moving in a plane and show that the motion can be resolved in two independent motions in mutually perpendicular directions.
Let \(\vec{u}\) be the initial velocity of a particle at an initial time ti = 0, \(\vec{a}\) its uniform (constant) acceleration, \(\vec{v}\) its final velocity at a final time tf = t, \(\vec{r_0}\) is the position vector at time ti, \(\vec{r}\) the position vector at time tf, and \(\vec{s}\) the displacement of the particle in the elapsed time Δt = tf — ti = t. Then,
\(\vec{a}\) = \(\frac{\vec{v}-\vec{u}}{t}\)
∴ \(\vec{v}\) = \(\vec{u}+\vec{a}t\) = …..(1)
\(\vec{s}\) = \((\vec{v_{av}})t\) = \(\frac{1}{2}(\vec{u}+\vec{v})t\)
= \(\frac{1}{2}(\vec{u}+\vec{u}+\vec{a}t)t\)
∴ \(\vec{s}\) = \(\vec{u}t+\frac{1}{2}\vec{a}t^2\) …..(2)
The dot product of Eq.(1) with itself gives
\(\vec{v}·\vec{v}\) = \((\vec{u}+\vec{a}t)·(\vec{u}+\vec{a}t)\)
= \(\vec{u}·\vec{u}+2\vec{u}·\vec{a}t+\vec{a}·\vec{a}t^2\)
∴ v2 = u2 + \(2\vec{a}·(\vec{u}t+\frac{1}{2}\vec{a}t^2)\)
Substituting from Eq. (2),
v2 = u2 + 2\(\vec{a}·\vec{s}\) ……..(3)
Equations (1), (2) and (3) are the kinematical equations (equations of motion) in vector form.
For a motion in an x-y plane (i.e., a two-dimensional motion), the component equations are
vx_= ux + axt ……(1a)
vy_= uy + ayt …..(1b)
sx = x — x0 = uxt + \(\frac{1}{2}\)axt2 ...(2a)
sy = y — y0 = uyt + \(\frac{1}{2}\)ayt2...(2b)
v2x = u2x + axsx ….(3a)
v2y = u2y + aysy …..(3b)
We can see that Eqs. (1a), (2a) and (3a) involve only the x-components of displacement, velocity and acceleration, while Eqs. (1b), (2b) and (3b) involve the y-components of these quantities.
Thus, a two-dimensional motion can be described by two exclusive components along two perpendicular directions.
(vi) Derive equations of motion graphically for a particle having uniform acceleration, moving along a straight line.
Consider a particle moving in a straight line with an initial velocity u and constant acceleration a. The v—t graph is a straight line with slope a and y-intercept u. With u and a both positive, the graph is as shown in Fig.
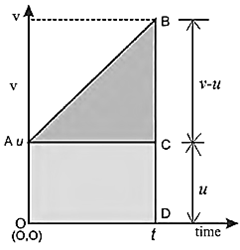
The slope of the line gives the acceleration of the particle,
a = \(\frac{dv}{dt}=\frac{v-u}{t-0}=\frac{v-u}{t}\)
∴ v = u + at
This is the first equation of motion (or the first kinematical equation).
The area under the ‘straight line for a time interval Δt = t − 0, as shown by the shaded region,
area of rect. OACD + area of Δ ABC
= (OA x AC) + \(\frac{1}{2}\)(AC x BC)
= ut + \(\frac{1}{2}\)t(v − u)
= ut +\(\frac{1}{2}\)at2 ( '.' v−u = at)
= s, distance covered in the elapsed time t.
∴ s = ut +\(\frac{1}{2}\)at2
This is the second equation of motion (or the second kinematical equation).
[Alternatively, the shaded area = area of the trapezium OABD = \(\frac{1}{2}\)(OA + BD) x OD
= \(\frac{1}{2}\)(v + u)t
= vav t { '.' vav = \(\frac{1}{2}\)(v + u)}
= distance covered in the elapsed time t]
∴ s = \(\frac{1}{2}(u+v)(\frac{v-u}{a})\)
substituting for t from the first kinematical equation. '
∴ s = \(\frac{v^2-u^2}{2a}\)
∴ v2 = u2 + 2as
This is the third equation of motion (or the third kinematical equation).
(vii) Derive the formula for the range and maximum height achieved by a projectile thrown from the origin with initial velocity at an angel θ to the horizontal.
If the projectile is launched with an initial velocity and a launch angle θ from the origin of the vertical x—y frame of reference containing the x and y components of the initial velocity are
ux = u cos θ, uy = u sin θ …… (1)
and those of the acceleration are
ax = 0, ay = −g ….(2)
(i) The vertical component of the instantaneous velocity is
vy = uy + ayt = u sin θ — gt ………(3)
The time of ascent (ta) is the time taken by the projectile to reach the peak of its trajectory where vy = 0. Hence, substituting t = ta and vy = 0 in the above equation (3),
ta = \(\frac{u\,sin\,θ}{g}\)
(ii) The time of flight (T) of a projectile is the time it takes to cover its entire trajectory or to cover its hofizontal range
The time of descent (td) is the time taken by the projectile to return to its initial launch height, usually the ground level, from the peak of its trajectory. It can be shown that td = ta.
∴ T = ta + td = 2ta = \(\frac{2u\,sin\,θ}{g}\)
(iii) The range or horizontal range R is the horizontal distance travelled by the projectile during its flight.
∴ R = uxT = \(\frac{2u_xu_y}{g}\)
= \(\frac{2(u\,sin\,θ)(u\,cos\,θ)}{g}\)
= \(\frac{u^2(sin\,θ\,cos\,θ)}{g}\)
∴ R = \(\frac{u^2sin\,2θ}{g}\) ….(4)
(iv) The vertical component of the displacement of the projectile at an instant t is
y = uyt − ½ gt2
At t= ta, the projectile is at its peak, i.e., at maximum height, y = H.
∴ H = uyta − \(\frac{1}{2}\)gt2a
= \(u_y(\frac{u_y}{g})-\frac{1}{2}g(\frac{u_y}{g})^2\)
= \(\frac{u_y^2}{2g}=\frac{u^2sin^2θ}{2g}\)
(viii) Show that the path of a projectile is a parabola.
Suppose a projectile is launched obliquely with an initial velocity , inclined at an angle θ to the horizontal, called the launch angle or the angle of projection, and that after launching no force, except that due to gravity, acts on it.
Then, the projectile's trajectory or path is confined to a vertical plane containing . Its acceleration, due only to gravity, is constant near the Earth's surface and always vertically downward. In the horizontal direction it is not acted upon by any force. Hence, along that direction, it has no acceleration, i.e., it moves with a constant velocity. We orient the x-axis horizontal and the y-axis vertical such that lies in the xy plane and take the launch point as the origin of the axes; the motion then lies in the xy plane. (For reference, see Fig.)
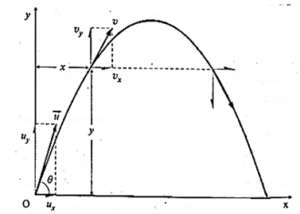
The x and y components of the kinematic variables are
(i) the initial velocity :
ux = u cos θ, uy = u sin θ …… (1)
(ii) the acceleration :
ax = 0, ay = −g ….(2)
(iii) the displacement :
x = uxt + \(\frac{1}{2}\)at2 = (u cos θ)t …….(3)
y = uyt + \(\frac{1}{2}\)ayt2
= (u sin θ)t − \(\frac{1}{2}\)gt2 ……(4)
From above Eq. (3), t = \(\frac{x}{u\,cos\,θ}\)
Substituting the value of t in Eq. (4),
y = \((u\,sin\,θ)\frac{x}{u\,cos\,θ}-\frac{1}{2}g(\frac{x}{u\,cos\,θ})^2\)
∴ y = x tan θ \(-(\frac{g}{2u^2\,cos^2\,θ})x^2\)
Since θ, u and g are the constants of the motion, the above equation is of the form y = bx — cx2, in which b and c are constants. This being the equation of a parabola, the trajectory of the projectile is a parabola.
(ix) What is a conical pendulum? Show that its time period is given by 2π\(\sqrt{\frac{L\,cos\,θ}{g}}\), where L is the length of the string, θ is the angle that the string makes with the vertical and g is the acceleration due to gravity.
Conical pendulum : A conical pendulum is a simple pendulum whose bob revolves in a horizontal circle with constant speed with the centre of its circular path below the point of suspension such that the string makes a constant angle θ with the vertical.
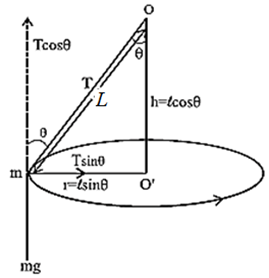
Expression :
Consider a conical pendulum of string length L with its bob of mass m performing UCM along a horizontal circle of radius r (Fig-7.).
The centre O’ of the circular path is vertically below the point of suspension O, and the string makes a constant angle θ with the vertical.
At every instant of its motion, the bob is acted upon by its weight m\(\vec{g}\) and the tension\(\vec{F}\) in the string. If the constant linear speed of the bob is v, the necessary horizontal centripetal force is
FC = mv2/r
\(\vec{F}\) is the resultant of the tension in the string and the weight. Resolve \(\vec{F}\) into components F cos θ vertically opposite to the weight of the bob and F sin θ horizontal. F cos θ balances the weight. F sin θ is the necessary centripetal force.
∴ F sin θ = mv2/r and
F cos θ = mg
Dividing Eq. (1) by Eq. (2),
tan θ = v2/rg ……(3)
The period T of the conical pendulum is the time taken by its bob to complete one revolution in a horizontal circle with constant speed v.
Then,
v = 2πr/T ….(4)
∴ tan θ = \(\frac{4π^2r^2}{T^2rg}\)=\(\frac{4π^2r}{T^2g}\)
∴ T2 = \(\frac{4π^2r}{g\,tan\,θ}\)= \(\frac{4π^2L\,sin\,θ}{g\,tan\,θ}\) ..(‘.’ r = L sin θ)
= \(\frac{4π^2L\,cos\,θ}{g}\)
∴ T = 2π\(\sqrt{\frac{L\,cos\,θ}{g}}\)=2π\(\sqrt{\frac{h}{g}}\) … (5)
where h = L cos θ is the axial height of the cone.
Equation (5) is the required expression.
(x) Define angular velocity. Show that the centripetal force on a particle undergoing uniform circular motion is −mω2 \(\vec{r}\) .
(i) Angular velocity : The time rate of angular displacement of a particle performing circular motion is called the angular velocity.
If the particle has an angular displacement δθ in a short time interval δt its angular velocity
\(\vec{ω} =\lim_{δt→0}\frac{\vec{δθ}}{dt}=\frac{\vec{dθ}}{dt}\)
is a vector in the direction of \(\vec{δθ}\), given by the right hand rule or right-handed screw rule.
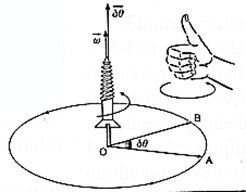
(ii) Consider a particle performing uniform circular motion with a constant angular velocity \(\vec{ω}\) along a circle in the xy plane. Let r be the radius of the circle and its centre be the origin of the coordinate axes. If the angular position of the particle at any instant t is θ as shown in the figure, then θ = ωt.
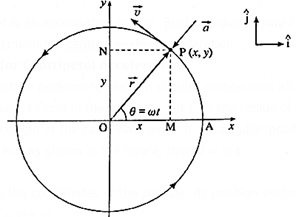
If x and y are the coordinates of the particle, its position vector or the radius vector at time t is \(\vec{r}=x\hat{i}+y\hat{j}\)
where \(\hat{i}\) and \(\hat{j}\) are unit vectors along the x and y axes respectively.
From Δ POM,
x =r cos θ = r cos ωt and
y = r sin θ = r sin ωt
∴ \(\vec{r}\) = r cos ωt \(\hat{i}\) + r cos ωt \(\hat{j}\)
The linear velocity of the particle is
\(\vec{v}=\frac{d\vec{r}}{dt}=\frac{d}{dt}\)(r cos ωt \(\hat{i}\) + r cos ωt \(\hat{j}\))
∴\(\vec{r}\) = −ωr sin ωt \(\hat{i}\) + ωr cos ωt \(\hat{j}\)
Since r and ω are constant in uniform circular motion is along the tangent to the path in the sense of motion of the particle.
The linear acceleration of the particle is
\(\vec{a}=\frac{d\vec{v}}{dt}=\frac{d}{dt}\)(−ωr sin ωt \(\hat{i}\) + ωr cos ωt \(\hat{j}\))
= −ω2r cos ωt \(\hat{i}\) − ω2r sin ωt \(\hat{j}\)
= −ω2(r cos ωt \(\hat{i}\) + r sin ωt \(\hat{j}\))
∴\(\vec{a}\)=−ω2\(\vec{r}\)
The acceleration of a particle performing UCM has the magnitude ω2r. The minus sign shows that its direction is opposite to that of \(\vec{r}\).
It means that at every instant the acceleration is directed along the radius towards the centre of the circle. This acceleration is called radial acceleration or centripetal acceleration.
A net real force must act on the particle to produce this acceleration. This force, which at every instant must point towards the centre of the circle, is called the centripetal force.
If m is the mass of the particle, the centripetal force,
\(\vec{F}\)= m\(\vec{a}\) = −mω2\(\vec{r}\)
Question 3.
Solve the following problems.
(i) An aeroplane has a run of 500 m to take off from the runway. It starts from rest and moves with constant acceleration to cover the runway in 30 sec. What is the velocity of the aeroplane at the take off ?
Given : s = 500 m, u = 0, constant acceleration, t = 30 s
Since acceleration is constant,
s = vavt = \((\frac{u+v}{2})=\frac{v}{2}t\) (‘.’ u = 0)
The velocity of the aeroplane at take off,
v = 2s/t = 2(500)/30 = 100/3 m/s
= \(\frac{100/1000\,km}{3/3600\,hr}=\frac{360}{3}\) = 120 km/h
(ii). A car moving along a straight road with a speed of 120 km/hr, is brought to rest by applying brakes. The car covers a distance of 100 m before it stops. Calculate (i) the average retardation of the car (ii) time taken by the car to come to rest.
Given : u = 120 km/h = (120×103 )/3600 m/s = 100/3 m/s, s = 100 m, v=0
(i) v2 = u2 + 2as = 0, as v = 0
∴ 2as = −u2
∴ a = −u2/2s
∴ a = \(-\frac{(100/3)^2}{2×100}\) = \(-\frac{100×100}{9×2×100}\)
= \(-\frac{50}{9}\) = − 5.556 m/s2
∴ The average retardation of the car
= −a = 5.556 m/s2
(ii) v = u + at = 0, as v = 0
∴ u = −at, ∴ t = —u/a
∴t = \(-\frac{(100/3)}{(-50/9)}\) = \(\frac{300}{50}\) = 6 s
This is the time taken by the car to come to rest
(iii) A car travels at a speed of 50 km/hr for 30 minutes, at 30 km/hr for next 15 minutes and then 70 km/hr for next 45 minutes. What is the average speed of the car?
Given : v1 = 50 km/h, t1 = 30 min =30/60 h = 0.5 h,
v2 = 30 krn/h, t2 = 15 min = 15/60 h = 0.25 h,
v3 = 70 km/h, t3 = 45 min = 45/60 h = 0.75 h
The average speed of the car,
v = \(\frac{s_1+s_2+s_3}{t_1+t_2+t_3}\) = \(\frac{v_1t_1+v_2t_2+v_3t_3}{t_1+t_2+t_3}\)
= \(\frac{50×0.5+30×0.25+70×0.75}{0.5+0.25+0.75}\)
= \(\frac{25+7.5+52.5}{1.5}=\frac{85}{1.5}\)
= 56.66 km/h
(iv) A velocity-time graph is shown in the adjoining figure.
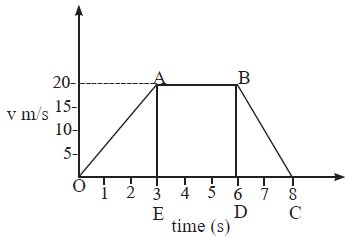
Determine:
(a) initial speed of the car
(b) maximum speed attained by the car
(c) part of the graph showing zero acceleration
(d) part of the graph showing constant retardation
(e) distance travelled by the car in first 6 sec.
(a) The initial speed (at t = 0) of the car = speed at O = 0 m/s.
(b) The maximum speed attained by the car = speed at A = 20 m/s.
(c) The car has zero acceleration (or constant speed) between t = 3 s and t = 6 s as shown by the part AB.
(d) In the 2 seconds time interval (t = 6 s to t= 8 s) in which the car decelerates, the part BC of the graph is a straight line showing that there is uniform (constant) retardation.
[Note : The car had varying speed in the regions OA and BC.]
(e) The distance travelled by the car in the first 6 seconds
= area under the curve OAB
= area of Δ OAE + area of rect. ABDE
= OE x AE + AB x AE
= x 3 x 20 + 3 x 20 = 30 + 60 = 90 m
(v) A man throws a ball to maximum horizontal distance of 80 meters. Calculate the maximum height reached.
Given: Rmax = 80 m
R = \(\frac{u^2\,sin\,2θ}{g}\) and H = \(\frac{u^2\,sin\,2θ}{2g}\)
The maximum range is attained for launch angle θ = 45°, so that sin 2θ = 1 and the maximum range of the projectile is
Rmax = u2/g
The corresponding maximum (peak) height is
H = \(\frac{u^2(sin\,45)^2}{2g}\) = \(\frac{u^2(\frac{1}{\sqrt{2}})^2}{2g}\) = u2/4g
∴ H = Rmax/4 = 80/4 = 20 m
(vi) A particle is projected with speed v0 at angle θ to the horizontal on an inclined surface making an angle Φ (Φ< θ ) to the horizontal. Find the range of the projectile along the inclined surface.
Suppose a particle is projected with an initial speed u = v0 and angle of projection θ from the bottom of an inclined surface whose angle of inclination with the horizontal is Φ, Fig.

Let the launch point be the origin of the vertical x-y frame of reference. The particle strikes the inclined surface at a point A. We have to find an expression for the range OA.
The equation of the trajectory of profile is given by
y = x tan θ − \((\frac{g}{2u^2\,cos^2θ})x^2\) …..(1)
In Δ OAB
R = OA = \(\frac{OB}{cosΦ}\) = \(\frac{x}{cosΦ}\)
∴ x = R cos Φ …..(2)
And R = OA = \(\frac{AB}{sinΦ}\) = \(\frac{y}{sinΦ}\)
∴ y = R sin Φ …..(3)
From eq. (1), (2) and (3)
R sin Φ = R cos Φ tan θ − \((\frac{g}{2v_0^2\,cos^2θ})\)R2cos2Φ ….(‘.’ u=v0)
∴ sin Φ = cos Φ tan θ − \((\frac{g}{2v_0^2\,cos^2θ})\)R cos2Φ
∴ \(\frac{gR\,cos^2Φ}{2v_0^2\,cos^2θ}\) = ( cos Φ tan θ - sin Φ )
Hence
R = \((\frac{2v_0^2\,cos^2θ}{g\,cos^2Φ})\)( cos Φ tan θ - sin Φ )
= \((\frac{2v_0^2\,cos\,θ}{g\,cos^2Φ})(\frac{cos\,θ\,cos\,Φ\,sin\,θ}{cos\,θ} - cos\,θ\,sin\,Φ)\)
= \((\frac{2v_0^2\,cos\,θ}{g\,cos^2Φ})\)( sin θ cos Φ − cos θ sin Φ )
= \((\frac{2v_0^2\,cos\,θ\,sin(θ-Φ)}{g\,cos^2Φ})\) ….[‘.’ sin θ cos ∅ − cos θ sin ∅ = sin(θ − ∅)]
(vii) A metro train runs from station A to B to C. It takes 4 minutes in travelling from station A to station B. The train halts at station B for 20 s. Then it starts from station B and reaches station C in next 3 minutes. At the start, the train accelerates for 10 sec to reach the constant speed of 72 km/hr. The train moving at the constant speed is brought to rest in 10 sec. at next station.
(a) Plot the velocity- time graph for the train travelling from the station A to B to C.
(b) Calculate the distance between the stations A, B and C.
Given :
| Time, t(s) | Speed, v(m/s) |
| 0 | 0 |
| 0-10 | Increase to 20 m/s |
| 10-230 | 20, constant |
| 230-240 | Decrease to 0 |
| 240-260 | 0 |
| 260-270 | Increase to 20 m/s |
| 270-430 | 20, constant |
| 430-440 | Decrease to 0 |
(a) v-t graph
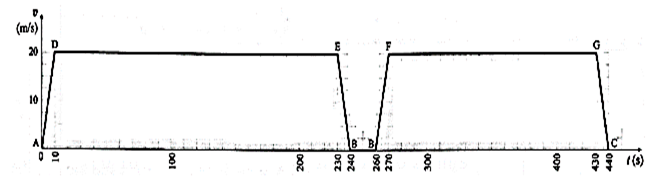
(b) Distances from the graph :
The distance between stations A and B = the shaded area ADEBA
= \(\frac{(240-0)+(230-10)}{2}×20\) = (240 + 220) x 10 = 4600 m = 4.6 km
The distance between stations B and C = the shaded area BFGCB
= \(\frac{(440-260)+(430-270)}{2}×20\) = (180 + 160) x 10 = 3400 m = 3 4 km
(viii) A train is moving eastward at 10 m/sec. A waiter is walking eastward at 1.2m/sec; and a fly is flying toward the north across the waiter’s tray at 2 m/s. What is the velocity of the fly relative to Earth.
Given : Speed of the train relative to the Earth, vTE = 10 m/s due east;
speed of the waiter relative to the train, vWT = 1.2 m/s due east;
speed of the fly relative to the waiter, vFW = 2 m/s due north
Using an xy coordinate system with the positive direction of x due east and that of y due north,
\(\vec{v}_{TE}=10\hat{i}\) m/s, \(\vec{v}_{WT}=1.2\hat{i}\) m/s, \(\vec{v}_{FW}=2\hat{j}\) m/s
The velocity of the fly relative to the Earth is
\(\vec{v}_{FE}=\vec{v}_{FW}+\vec{v}_{WT}+\vec{v}_{TE}\)
= 2\(\hat{j}\) + 1.2\(\hat{i}\) + 10\(\hat{i}\)
= (11.2\(\hat{i}\) + 2\(\hat{j}\)) m/s
|\(\vec{v}_{FE}\)| = \(\sqrt{(11.2)^2+(2)^2}\)
= \(\sqrt{125.44+4}\)
= 11.38 m/s
tan θ = 2/11.2 = 0.1786
∴ θ = tan-1 0.1786 = 10°7'
The velocity of the fly relative to the Earth is (11.2\(\hat{i}\) + 2\(\hat{j}\)) m/s, i.e., 11.38 m/s in the direction of 10°7' north of east.
(ix) A car moves in a circle at the constant speed of 50 m/s and completes one revolution in 40 s. Determine the magnitude of acceleration of the car.
Given: v = 50 m/s, T= 40s
The magnitude of the acceleration of the car = a
= v ω
= v\((\frac{2π}{T})\) ...( \(ω=\frac{2π}{T}\)
= 50\((\frac{2×3.142}{40})\) = \((\frac{50}{20})\)(3.142)
= 2.5 x 3.142 = 7.855 m/s2
(x) A particle moves in a circle with constant speed of 15 m/s. The radius of the circle is 2 m. Determine the centripetal acceleration of the particle.
Given : v = 15 m/s, r =2m
The centripetal acceleration of the particle
= a = v2/r = (15)2/2
= 225/2
= 112.5 m/s2
(xi) A projectile is thrown at an angle of 30° to the horizontal. What should be the range of initial velocity (u) so that its range will be between 40m and 50 m? Assume g = 10 m s-2.
Given:
θ = 30°, R1 = 40m, R2 =50 m, g = 10 m/s2
R = \(\frac{u^2\,sin\,2θ}{g}\)
∴ u2 = \(\frac{Rg}{sin60°}\) = \(\frac{10R}{\sqrt{3}/2}\)
∴ u2 = \(\frac{20R}{\sqrt{3}}\)
For R = R1,
u12 = \(\frac{20×40}{\sqrt{3}}\) = = \(\frac{800}{\sqrt{3}}\) = 461.9 (m/s)2
∴ u1 = 21.49 m/s
As u2 = \(\frac{20R}{\sqrt{3}}\)
\(\frac{u_2^2}{u_1^2}=\frac{R_2}{R_1}=\frac{50}{40}\) = 1.25
∴ u22 = 1.25 u12 = (1.25)(461.9) = 577.3 (m/s)2
∴ u2 = 24.03 m/s
21.49 ≤ u ≤ 24.03 m/s
This is the required range of the initial (i.e launch) velocity.
Main Page : – Maharashtra Board Class 11th-Physics – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter 2: Mathematical Methods – Online Solutions
Next Chapter : Chapter 4: Laws of Motion – Online Solutions
We reply to valid query.