Electrostatics
Maharashtra Board-Class-12th-Physics-Chapter-8
Notes-Part-2
Topics to be Learn : Part-2
|
Equipotential Surfaces :
Equipotential surface : An equipotential surface is that surface, at every point of which the electric potential is the same.
Electric field lines and equipotential surfaces are always mutually perpendicular. In a diagram, only a few representative equipotentials are shown, usually with equal potential differences between adjacent surfaces.
Equipotential surfaces for different potentials do not touch or intersect since a point cannot be at two electric potentials simultaneously.
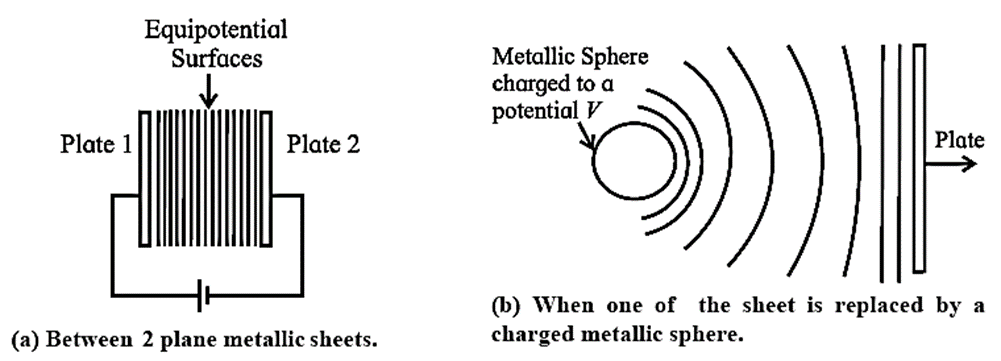
Case 1 : For the special case of a uniform field, in which the field lines are equally-spaced parallel lines, the equipotentials are parallel planes perpendicular to the field lines, Fig.
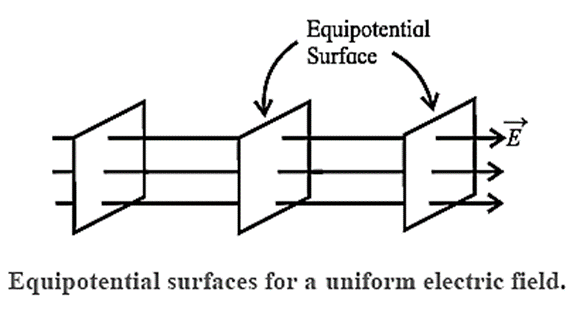
- For equal potential differences between adjacent planes, these equipotential are equally spaced.
Case 2 : For the special case of a single point charge, for which the field lines are radial, the equipotential are concentric spheres centred on the point charge, Fig.
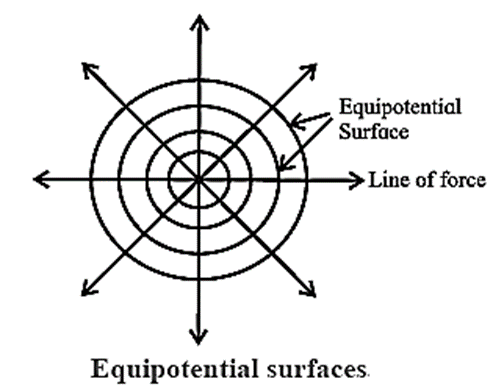
For a given point charge q.
V = C/r
where C = \(\frac{q}{4πε_0}\) is a constant. Since 1/r is not a linear function of r, equipotentials with equal potential differences between adjacent surfaces are not evenly spaced in radius.
- For a negative point charge, the direction of electric field lines would be reversed, coverging at the charge. There would be no change in the shape of the equipotential surfaces, except that they would correspond to negative potentials.
Electric field lines and equipotential surfaces are always mutually perpendicular :
Explanation :
If a test charge q0 is moved on an equipotential surface of potential V, the electric potential energy U = q0V remains constant. Because U does not change as q0 is moved, the work done by the electric field on q0 must be zero.
If is the electric field on the surface,
dW = \(\vec{F}.\vec{dx}\) = \(q_0\vec{F}.\vec{dx}\) = \(q_0\vec{E}cos θ\) = 0
∴ cos θ = 0 or θ = 900
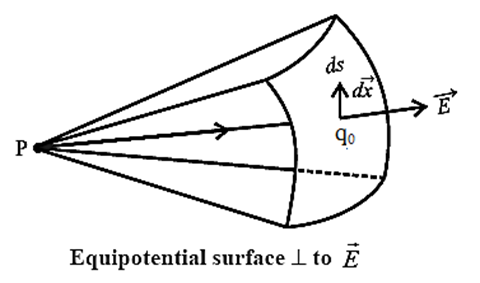
Hence, the electric force \(q_0\vec{E}\) is always perpendicular to the displacement of a charge moving on an equilateral surface. Thus, electric field lines and equipotential surfaces are always mutually perpendicular.
- Note that if \(\vec{E}\) is not perpendicular to a equipotential surface everywhere, it would have a nonzero component along the surface. So to move a test charge against this component work would have to be done. But by the definition of equipotential surfaces, there is no potential difference between any two points on an equipotential surface and hence no work is required to displace the charge on the surface. Therefore, we can conclude that the electrostatic field must be normal to the equipotential surface at every point, and vice versa.
Diagrams :
(a) A pair of charged parallel metal plates sets up a uniform electric field between the plates, away from its edges, as shown by their even spacing. The field is perpendicular to the plates, in the direction from the positive plate toward the negative plate. Conductors are equipotential surfaces, so the negative plate is an equipotential surface with potential taken as zero and the positive plate is an equipotential surface with potential = V. The equipotential surfaces between the plates are parallel to the plates. Electric field lines and equipotential surface.
Advantages of using electrostatic potential :
- The electrostatic potential at each point in space in the vicinity of the source charges represents a scalar field.
- The advantages of electrostatic potential field associated with a given distribution of charges are as follows :
- If we know the potential difference between any two points, we can easily obtain the change in potential energy and the work done when a charge placed in the field moves between these two points.
- Electric field is a vector field. Electrostatic potential being a scalar field, the potential at any point due to several charges is simply the algebraic sum of the potentials due to the individual charges.
- The construction of equipotential surfaces helps to visualize the electric field pattern.
- It is possible to calculate the electric field from the scalar potential field function V (by differentiating V with respect to the space coordinates.)
Electrical Energy of Two Point Charges and of a Dipole in an Electrostatic Field:
When two like charges lie infinite distance apart, their potential energy is zero because no work has to done in moving one charge at infinite distance from the other. But when they are brought closer to one another, work has to be done against the force of repulsion.
As electrostatic force is conservative, this work gets stored as the potential energy of the two charges.
Electrostatic potential energy of a system of point charges is defined as the total amount of work done to assemble the system of charges by bringing them from infinity to their present locations.
(a) Potential energy of a system of 2 point charges:
Let us consider 2 charges q1 and q2 with position vectors r1 and r2 relative to some origin (O).
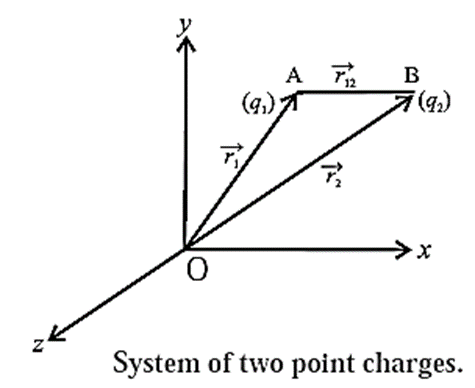
To calculate the electric potential energy of the two charge system, we assume that the two charges q1 and q2 are initially at infinity.
We then determine the work done in bringing the charges to the given location by an external agency.
In bringing the first charge q1 to position A(\(\vec{r_1}\)) no work is done because there is no external field against which work needs to be done as charge q2 is still at infinity i.e., W1 = 0. This charge produces a potential in space given by
V1 = \(\frac{1}{4πε_0}\frac{q_1}{r_1}\) ……..(1)
Where r1 is the distance of point A from the origin.
When we bring charge q2 from infinity to B (\(\vec{r_2}\) at a distance r12, from q1, work done is
W2 = (potential at B due to charge q1) × q2
= \(\frac{1}{4πε_0}\frac{q_1}{r_{12}}×q_2\) ...(where AB = r12) ……..(1)
This work done in bringing the two charges to their respective locations is stored as the potential energy of the configuration of two charges.
Hence, the total work done is
W = W1 + W2 = 0 +\(\frac{1}{4πε_0}\frac{q_1q_2}{r_{12}}\)
= \(\frac{1}{4πε_0}\frac{q_1q_2}{r_{12}}\)
Since the charges were always kept in equilibrium, the change in the potential energy Uf − Ui equals W.
Since the charges were brought from infinity where their potential energy is assumed to be zero, U1 = 0. Therefore, the potential energy of the system of two point charges is
U = Uf = \(\frac{1}{4πε_0}\frac{q_1q_2}{r_{12}}\)
(b) Potential energy for a system of N point charges:
Consider assembling a configuration of N point charges q1, q2, q3,... , qN at points A, B, C, D,…, respectively, in a region free of external electric field.
Let \(\vec{r_1}\), \(\vec{r_2}\), \(\vec{r_3}\), ......\(\vec{r_N}\) be the position vectors of the points A, B, C, D,… etc., respectively, with respect to an arbitrary reference frame.
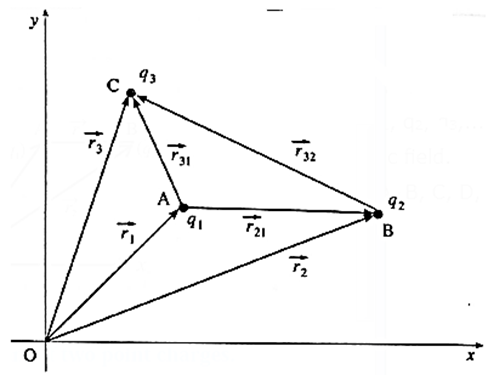
A configuration of three point charges (For reference only)
No work is done in bringing the first charge q1 from infinity to point A, so W1 = 0. Subsequently, the potential at B is
VB = \(\frac{1}{4πε_0}\frac{q_1}{r_{21}}\)
where r21 =|\(\vec{r}_{21}\)|, \(\vec{r}_{21}\) = \(\vec{r_2}-\vec{r_1}\) being the position vector of B with respect to A. Consequently, the work done by an external agent in bringing q2 from infinity to B in the electric field of q1 is
W2 = VB.q2 = \(\frac{1}{4πε_0}\frac{q_1q_2}{r_{21}}\)
Subsequently, the potential at C is
VC = V1 + V2
where V1 and V2 are the potentials due to q1 and q2.
V1 = \(\frac{1}{4πε_0}\frac{q_1}{r_{31}}\), V2 = \(\frac{1}{4πε_0}\frac{q_2}{r_{32}}\),
Where r31 =|\(\vec{r}_{31}\)|, \(\vec{r}_{31}\) = \(\vec{r_3}-\vec{r_1}\) and r32 =|\(\vec{r}_{32}\)|, \(\vec{r}_{32}\) = \(\vec{r_3}-\vec{r_2}\)
∴ VC = \(\frac{1}{4πε_0}(\frac{q_1}{r_{31}}+\frac{q_2}{r_{32}})\)
Consequently, the work done by the external agent in bringing the third charge q3 from infinity to C in the electric fields of q1 and q2 is
W3 = VC.q3 = \(\frac{1}{4πε_0}(\frac{q_1q_3}{r_{31}}+\frac{q_2q_3}{r_{32}})\)
Now, the potential at D is
VD = V1 + V2 + V3 = \(\frac{1}{4πε_0}(\frac{q_1}{r_{41}}+\frac{q_2}{r_{42}}+\frac{q_3}{r_{43}})\)
And W4 = VD.q4 = \(\frac{1}{4πε_0}(\frac{q_1q_4}{r_{41}}+\frac{q_2q_4}{r_{42}}+\frac{q_3q_4}{r_{43}})\)
Hence, the total work done in assembling N point charges is
W = W1 + W2 + W3 + W4+ .... .. +WN.
= \(\frac{1}{4πε_0}[\sum_{j=1\,to\,N-1,J≠k}(\sum_{k=2\,to\,N})\frac{q_jq_k}{r_{kj}}]\)
= Uf − Ui
Since the charges were brought from infinity where the potential energy is assumed to be zero, Ui = 0. Therefore, the potential energy of the configuration of N point charges is
U = Uf = \(\frac{1}{4πε_0}[\sum_{j=1\,to\,N-1,J≠k}(\sum_{k=2\,to\,N})\frac{q_jq_k}{r_{kj}}]\) = \(\frac{1}{4πε_0}[\sum_{\text{all pairs}}\frac{q_jq_k}{r_{kj}}]\)
(c) Potential energy of a single charge in an external field:
If V (\(\vec{r}\)) is the external potential at any point P having position vector\(\vec{r}\), then by definition, work done in bringing a unit positive charge from ∞ to the point P is equal to V.
∴ Work done in bringing a charge q, from ∞ to the given point in the external field is qV (\(\vec{r}\))
This work is stored in the form of potential energy of a system of charge q.
∴ PE of a system of a single charge q at in an external field is given by
PE = U(\(\vec{r}\)) = qV(\(\vec{r}\))
where it is assumed that q is sufficiently small and does not significantly distort the electric field and the potential at the point.
(d) Potential energy of a system of two charges in an external field:
Consider assembling a system of two point charges q1 and q2 at points A and B, respectively, in a region of external electric field.

Let \(\vec{r_1}\) and \(\vec{r_2}\) be the position vectors of A and B, respectively, with respect to an arbitrary reference frame. \(\vec{r}_{21}\) =\(\vec{r_2}-\vec{r_1}\) is the position vector of B with respect to A.
Let V1 and V2 be the electric potentials of A and B due to the external field.
The work done in bringing the charge q1 from infinity to A against the electric force of the external field is
W1 = T1V1
Subsequently, the electric potential at B is
VB = V2 + V’(due to q1)
= V2 + \(\frac{1}{4πε_0}\frac{q_1}{r_{21}}\)
where r21=|\(\vec{r}_{21}\)|.
Consequently, the work done in bringing the second charge q2 from infinity to B is
W2 = q2VB
= q2V2 + \(\frac{1}{4πε_0}\frac{q_1q_2}{r_{21}}\)
Hence, the total work done by an external agent in assembling the two point charges in a region of external electric field is
W = W1 + W2
= q1V1 + q2V2 + \(\frac{1}{4πε_0}\frac{q_1q_2}{r_{21}}\)
Since the charges were always kept in equilibrium, the change in the potential energy of the system Uf − Ui = W. Also, since the charges were brought from infinity where their potential energy is assumed to be zero, Ui = 0. Therefore, the potential energy of the system of two charges in an external field is
U = Uf = q1V1 +q2V2 + \(\frac{1}{4πε_0}\frac{q_1q_2}{r_{21}}\)
(e) Potential energy of a dipole in an external field:
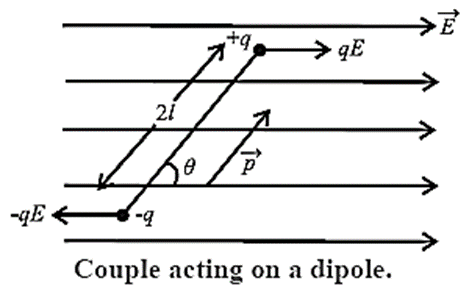
Consider a dipole with charges -q and +q separated by a finite distance 2l, placed in a uniform electric field \(\vec{E}\). It experiences a torque \(\vec{τ}\) which tends to rotate it.
\(\vec{τ}=\vec{P}×\vec{E}\) or τ = pE sin θ
In order to neutralize this torque, let us assume an external torque is applied, which rotates it in the plane of the paper from angle θ0 to angle θ, without angular acceleration and at an infinitesimal angular speed. Work done by the external torque
W = \(\int_{θ}^{θ}τ_{ext}(θ)dθ\)=\(\int_{θ}^{θ}pE\,sinθ\,dθ\)
= pE\([-cosθ]_{θ_0}^{θ}\)
= pE[−cos θ − (−cos θ0)]
= pE[−cos θ + cos θ0]
= pE[cos θ0 − cos θ]
This work done is stored as the potential energy of the system in the position when the dipole makes an angle θ with the electric field. The zero potential energy can be chosen as per convenience. We can choose U(θ0 ) = 0, giving
∴ U(θ) − U(θ0 ) = pE[cos θ0 − cos θ]
a) If initially the dipole is perpendicular to the field \(\vec{E}\) i.e., θ0 = π/2
U(θ) = pE[cos π/2 − cos θ]
= − pE cos θ
∴ U(θ) = \(-\vec{p}.\vec{E}\)
b) If initially the dipole is parallel to the field \(\vec{E}\) then θ0 = 0 and cos θ0 = 1
∴ U(θ) = pE[1 − cos θ]
Conductors and Insulators, Free Charges and Bound Charges Inside a Conductor:
Conductors and Insulators:
Materials or substances contain a large number of free charge carriers (free electrons) which allow electricity to flow through them are called the conductors.
In a metal the outer (valence) electrons are loosely bound to the nucleus and are thus free for conductivity, when an external electric field is applied.
Reasons of shocks : Metals, humans, earth and animal bodies are all conductors. The main reason we get electric shocks is that being a good conductor our human body allows a resistance free path for the current to flow from the wire to our body.
- During electric shock we experience an extreme stimulation of nerves and muscles. It needs a minimum of 1 mA of electric current to pass through our body for us to experience a shock.
- The danger of electric shock arises not from mere contact with a live wire but rather from simultaneous contact with a live wire and another body of wire at a different potential so that our body provides a conducting path between the two and current passes through our body.
- Touching a single wire by the birds does not result in a current through their bodies because then the electric circuit is not complete.
- But if a person touches two wires at different potentials at once, or if a bare-footed person touches the live wire only, the electric circuit is complete and the person receives an electric shock. In the latter case, the current from the wire passes to the Earth through the body.
Properties of conductors under electrostatic conditions :
Under electrostatic conditions the conductors have following properties.
- In the interior of a conductor, net electrostatic field is zero.
- Potential is constant within and on the surface of a conductor.
- In static situation, the interior of a conductor can have no charge.
- Electric field just outside a charged conductor is perpendicular to the surface of the conductor at every point.
- Surface charge density of a conductor could be different at different points.
Electrostatic shielding
The use of a conducting box to protect sensitive instruments from stray electric fields, or the use of a conducting wire cage to protect a person near a high-voltage installation or from lightning strike, is called electrostatic shielding
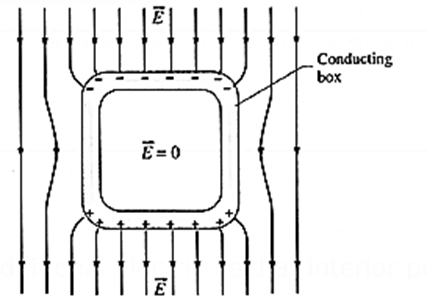
- When an isolated conductor, uncharged or charged, is placed in an external electric field, as in Fig. all points of the conductor come to the same potential. The free conduction electrons in the conductor distribute themselves on the surface, leaving a net positive charge on some regions of the surface and a net negative charge on other regions.
- This charge distribution causes an additional electric field at interior points such that the total field at every point inside is zero.
- The charge distribution on the conductor is such that the net electric field at all points on the surface to be perpendicular to the surface, thereby altering the shapes of the field lines near the conductor.
- During lightning and thunder storm it is always advisable to stay inside the car than near a tree in open ground, since the car acts as a shield.
Faraday cage :
The hollow conductor or the conducting wire cage that shields its interior from external electric fields is called a Faraday cage or Faraday shield
- A Faraday Cage, made from a contiguous metal sheet or from a fine metal mesh, is used to shield its content or occupant from static and nonstatic electric fields.
- Electro-magnetic shielding: MRI scanning rooms are built in such a manner that they prevent the mixing of the external radio frequency signals with the MRI machine.
Free charges and Bound charges inside materials:
Bound charges : In a material, the inner shell electrons are tightly bound to their respective nuclei and together they have fixed lattice positions. They are called bound charges.
- In insulators, all inner shell and outer shell electrons are tightly bound to their respective nuclei so that even at room temperature the number of free charges is several orders lower than that in a metallic conductor. Hence, they are poor conductors of electricity and heat.
- In the absence of free conduction electrons, excess charges transferred to an insulator remain localized. An insulator can have non-zero surface charge density as well as volume charge density.
Free charges or free electrons :In metals, the outermost valence electrons are loosely bound to their respective nucleus and, due to the regular atomic arrangement in a lattice, are set free to move inside the metal. They are called free charges or free electrons.
- Under an applied electric field, the free electrons drift in a direction opposite to the electric field and constitute an electric current in the metal.
- In electrolytes, electrical dissociation of ionic molecules results in both positive and negative free charges, and electric conduction is due to both types of tree charges.
- Under electrostatic conditions, excess charges reside only on the surface of a conductor.
Dielectrics and Electric Polarisation:
Dielectrics : Dielectrics are insulates which can be used to store electrical energy. When dielectric substances are placed in an external field, their positive and negative charges get displaced in opposite directions and the molecules develop a net dipole moment. This is called polarization of the material and such materials are called dielectrics.
- A dielectric can sustain a high electric field up to a certain limit. An ideal dielectric has no free charges.
Important commercial dielectrics are of two types, polar and nonpolar.
Examples :
- Polar dielectrics : Silicones, halogenated hydrocarbons.
- Nonpolar dielectrics : (1) Ceramics, glasses, plastics (polyethylene, polystyrene, etc.) mica paper. (2) Liquid : Mineral oils.
Polar dielectrics :
A molecule in which the centre of mass of positive charges (protons) does not coincide with the centre of mass of negative charges (electrons), because of the asymmetric shape of the molecules is called polar molecule. see Fig.
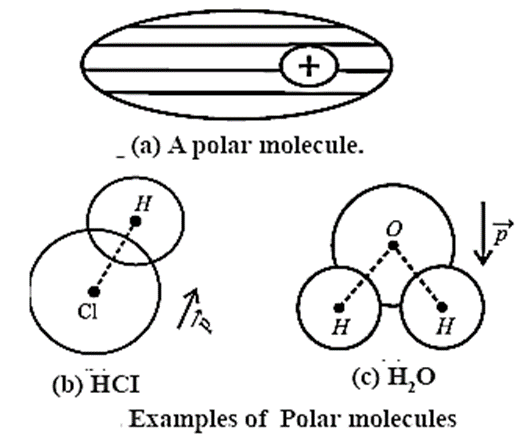
- Dipole moments of polar molecules are of the order of 10−30 C-m.
- Water molecule has a bent shape with its two O - H bonds which are inclined at an angle of about 105°. It has a very high dipole moment of 6.1 × 10-30 C.m.
- Examples : Gaseous hydrogen halides (HF, HCl,etc.); NH3, NO3, N2O, water molecules; all hetero-nuclear diatomic molecules (with any covalent bond between two different atoms).
Non Polar dielectrics:
A molecule in which the centre of mass of the positive charges coincides with the centre of mass of the negative charges is called a non polar molecule. see Fig. (a).

These have symmetrical shapes and have zero dipole moment in the normal state.
Polarization of a non-polar dielectric in an external electric field:
In the absence of an external electric field, the molecules of a nonpolar dielectric have no inherent electric dipole moments. An applied electric field slightly separates the centres of negative and positive charges. Then, a nonpolar molecule acquires an induced dipole moment in the direction of the applied field, as shown in Fig.
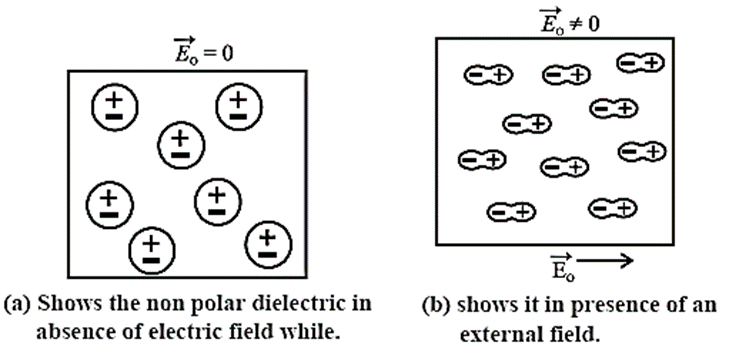
The induced dipole moments of all the molecules add up giving the dielectric a net induced electric dipole moment in the presence of the applied field.
Polarization of a polar dielectric in an external electric field:
In the absence of an external electric field, the permanent electric dipole moments of the molecules of a polar dielectric orient in random directions due to thermal agitation such that their vector sum is zero, see below Fig. (a).
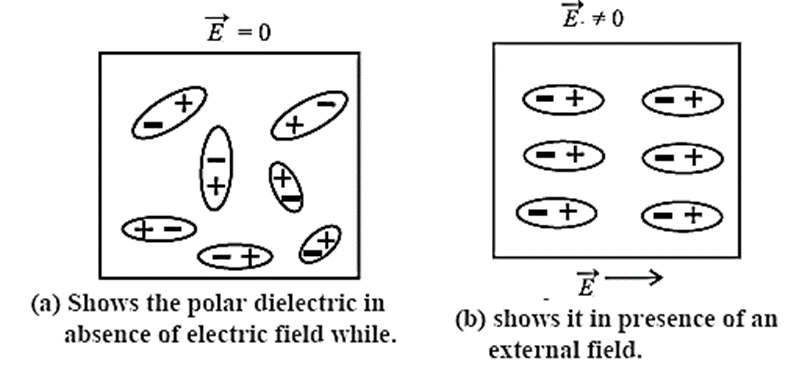
An applied electric field does slightly increases the separation between the centres of negative and positive charges. But, a much larger effect is the tendency of the dipole moments to align with the field, although thermal agitation prevents complete alignment, as shown in above Fig. (b).
- Due to the partial alignment of the dipole moments, a polar dielectric also acquires a net induced electric dipole moment in the direction of the applied field.
- The extent of polarisation depends on the relative values of the two opposing tendencies: (1) the tendency of the applied field to align the dipoles (2) thermal agitation that tends to randomize.
Linear isotropic dielectric : A linear isotropic dielectric is one which when placed in a uniform electric field acquires an induced electric dipole moment in the direction of the field and proportional to the applied electric field intensity.
- Examples : Mica, glass.
Electric polarization in dielectrics : The electric polarization at every point within a dielectric is defined as the electric dipole moment per unit volume. It has the direction of the external electric field.
Electric susceptibility : In a linearly isotropic dielectric placed in a uniform electric field, the electric polarization \(\vec{P}\) is directly proportional to the electric field intensity \(\vec{E}\) inside the dielectric.
∴ \(\vec{P}\) = χeε0\(\vec{E}\)
where the proportionality constant χe, a positive quantity, is called the electric susceptibility of the dielectric.
It describes the electrical behaviour of a dielectric. It has different values for different dielectrics.
For vacuum χe = 0.
Note : χe is dimensionless. SI units of P and E are C/m2 and N/C.
Reduction of electric field due to polarization of a dielectric:
When a dielectric is placed in an external electric field, the value of the field inside the dielectric is less than the external field as a result of polarization.
Consider a rectangular slab of a linear isotropic dielectric placed in a uniform external electric field. In case of a nonpolar dielectric, the applied field slightly separates the centres of negative and positive charge in a molecule inducing an electric dipole moment in the direction of the field. In most cases, this separation is a very small fraction of a molecular diameter. In case of a polar dielectric, the permanent dipole moments of its molecules are partially aligned with the field. In either case, the dielectric is said to become polarized.
In a uniformly polarized dielectric, the charges of adjacent interior dipoles add to zero. But due to the unbalanced positive ends of dipoles at one face of the slab, bound positive charge appears on that exterior surface. Similarly, bound negative charge appears on the opposite exterior surface of the slab. These bound surface charges are called polarization charges. There is, however, no excess charge in any volume element within the slab and the slab as a whole remains electrically neutral.
The external electric field \(\vec{E_0}\) polarizes the dielectric, with a net polarization \(\vec{P}\) parallel to \(\vec{E_0}\). Within the dielectric, the induced field \(\vec{E_P}\) = \(-\frac{\vec{P}}{ε_0}\) due to the polarization charges is opposite to the applied field, see Fig.

\(\vec{E}\) = \(\vec{E_0}\)+\(\vec{E_P}\) = \(\vec{E_0}\)\(-\frac{\vec{P}}{ε_0}\)
i.e. E = E0 − EP in magnitude
Assuming the dielectric to be isotropic and linear,
\(\vec{P}\)= χeε0\(\vec{E}\)
where χe is the electric susceptibility of the dielectric.
∴ \(\vec{E_0}\) = (1 + χe)\(\vec{E}\) = k\(\vec{E}\)
where k = 1 + χe is the dielectric constant. This implies E = E0/k, thus less than E0. Thus, the effect of a dielectric material is always to decrease the electric field below the applied electric field.
Know This :
|
Main Page : – Maharashtra Board Class 12th-Physics – All chapters notes, solutions, videos, test, pdf. Previous Chapter : Chapter-7-Wave Optics –Online Notes Next Chapter : Chapter-9-Current Electricity – Online Notes
We reply to valid query.