Laws of Motion
Maharashtra Board-Class-11-Science-Physics-Chapter-4
Solutions
Question 1.
Choose the correct answer.
(i) Consider following pair of forces of equal magnitude and opposite directions:
- (P) Gravitational forces exerted on each other by two point masses separated by a distance.
- (Q) Couple of forces used to rotate a water tap.
- (R) Gravitational force and normal force experienced by an object kept on a table.
For which of these pair/pairs the two forces do NOT cancel each other’s translational effect?
(A) Only P (B) Only P and Q
(C) Only R (D) Only Q and R
(A) Only P
(ii) Consider following forces:
- (w) Force due to tension along a string,
- (x) Normal force given by a surface,
- (y) Force due to air resistance and
- (z) Buoyant force or upthrust given by a fluid.
Which of these are electromagnetic forces?
(A) Only w, y and z
(B) Only w, x and y
(C) Only x, y and z
(D) All four.
(D) All four.
(iii) At a given instant three point masses m, 2m and 3m are equidistant from each other. Consider only the gravitational forces between them. Select correct statement/s for this instance only:
(A) Mass m experiences maximum force.
(B) Mass 2m experiences maximum force.
(C) Mass 3m experiences maximum force.
(D) All masses experience force of same magnitude.
(C) Mass 3m experiences maximum force.
(iv) The rough surface of a horizontal table offers a definite maximum opposing force to initiate the motion of a block along the table, which is proportional to the resultant normal force given by the table. Forces F1 and F2 act at the same angle θ with the horizontal and both are just initiating the sliding motion of the block along the table.
Force F1 is a pulling force while the force F2 is a pushing force. F2 > F1 , because
(A) Component of F2 adds up to weight to increase the normal reaction.
(B) Component of F1 adds up to weight to increase the normal reaction.
(C) Component of F2 adds up to the opposing force.
(D) Component of F1 adds up to the opposing force.
(A) Component of F2 adds up to weight to increase the normal reaction.
(v) A mass 2m moving with some speed is directly approaching another mass m moving with double speed. After some time, they collide with coefficient of restitution 0.5. Ratio of their respective speeds after collision is
(A) 2/3
(B) 3/2
(C) 2
(D) ½
(B) 3/2
(vi) A uniform rod of mass 2m is held horizontal by two sturdy, practically inextensible vertical strings tied at its ends. A boy of mass 3m hangs himself at one third length of the rod. Ratio of the tension in the string close to the boy to that in the other string is
(A) 2
(B) 1.5
(C) 4/3
(D) 5/3
(B) 1.5
(vii) Select WRONG statement about centre of mass:
(A) Centre of mass of a ‘C’ shaped uniform rod can never be a point on that rod.
(B) If the line of action of a force passes through the centre of mass, the moment of that force is zero.
(C) Centre of mass of our Earth is not at its geometrical centre.
(D) While balancing an object on a pivot, the line of action of the gravitational force of the earth passes through the centre of mass of the object.
(D) While balancing an object on a pivot, the line of action of the gravitational force of the earth passes through the centre of mass of the object.
(viii) For which of the following objects will the centre of mass NOT be at their geometrical centre?
(I) An egg
(II) a cylindrical box full of rice
(III) a cubical box containing assorted sweets
(A) Only (I)
(B) Only (I) and (II)
(C) Only (III)
(D) All, (I), (II) and (III).
(D) All, (I), (II) and (III).
Question 2.
Answer the following questions.
(i) In the following table, every entry on the left column can match with any number of entries on the right side. Pick up all those and write respectively against A, B, C and D.
| Name of the force | Type of the force |
| Force due to tension in a string | EM force |
| Normal force | Reaction force |
| Frictional force | Conservative force |
| Resistive force offered by air or water for objects moving through it. | Non conservative force |
| Name of the force | Type of the force |
| Force due to tension in a string | EM force, Reaction force, Non conservative force |
| Normal force | EM force, Reaction force, Non conservative force |
| Frictional force | EM force, Reaction force, Non conservative force |
| Resistive force offered by air or water for objects moving through it. | EM force, Non conservative force |
(ii) In real life objects, never travel with uniform velocity, even on a horizontal surface, unless something is done? Why is it so? What is to be done?
A real object on a horizontal surface stops moving because of the presence of resistive forces of friction or viscous drag. For its continued motion, an external force is required to overcome these resistive forces.
(iii) For the study of any kind of motion, we never use Newton’s first law of motion directly. Why should it be studied?
Newton's first law of motion is not dismissed for two reasons :
- Before Newton synthesized and firmly founded that branch of mechanics called dynamics, Artistotelians had a different view of the role of force. They held that force was the cause of uniform (unaccelerated) motion. Newton's first law of motion implies that a net force is the cause of change of velocity. Thus, the first law was an accepted emphasis on the changing point of view in mechanics.
- Newton's first law defines inertial frames of reference and limits the scope of the second law to such frames. In deriving the first law from the second law, \(\vec{v}\) is assumed to be measured in an inertial frame; i.e., Newton's first law is built into the argument and not truly ‘derived’ from the second law. The first law is independent and necessary to understand Newton's concept of force. The argument that the first law is redundant, as some sceptics would like to impress upon us, is a deceptive fallacy.
(iv) Are there any situations in which we cannot apply Newton’s laws of motion? Is there any alternative for it?
Limitation of Newton’s laws of motion
- Newton’s laws are applicable only in the inertial frames of reference which they define. If the body is in a frame of reference of acceleration (a), we need to use a pseudo force (−m ) in addition to all the other forces while writing the force equations.
- Newton’s laws are applicable for point objects.
- Newton’s laws are applicable to rigid bodies. A body is said to be rigid if the relative distances between its particles do not change for any deforming force.
- For objects moving with speeds comparable to that of light, Newton’s laws of motion do not give results that match with the experimental results and Einstein's special theory of relativity has to be used.
- Behaviour and interaction of objects having atomic or molecular sizes cannot be explained using Newton’s laws of motion, and quantum mechanics has to be used.
(v) You are inside a closed capsule from where you are not able to see anything about the outside world. Suddenly you feel that you are pushed towards your right. Can you explain the possible cause (s)? Is it a feeling or a reality? Give at least one more situation like this.
The push to the right is due to the acceleration of the observer's frame of reference – the capsule — to the left. This could be due to an acceleration of the capsule in a straight line towards the left or due to the circular motion of the capsule, in which case it is the centripetal acceleration.
The force to the right is a reality in the observer's reference frame.
Similar pseudo force is experienced in a lift which accelerates up or down, and in an accelerating vehicle.
(vi) Among the four fundamental forces, only one force governs your daily life almost entirely. Justify the statement by stating that force.
Majority of forces experienced in our daily life, such as force of friction, normal reaction, tension in strings, collision forces, elastic forces, viscosity (fluid friction), etc. are EM in nature.
Thus, the electromagnetic force, the second strongest of the four fundamental forces, almost governs our daily life.
(vii) Find the odd man out:
(a) Force responsible for a string to become taut on stretching
(b) Weight of an object
(c) The force due to which we can hold an object in hand.
Answer :
(b) Weight of an object, it is due to the gravitational force of the Earth. The other two - tension in a string and friction — are electromagnetic in origin.
(viii) You are sitting next to your friend on ground. Is there any gravitational force of attraction between you two? If so, why are you not coming together naturally? Is any force other than the gravitational force of the earth coming in picture?
The attraction of gravity is universal. The gravitational forces between ordinary uncharged objects, on the other hand, are hidden by frictional forces of one type or another, or by the enormously higher gravitational force owing to the Earth. As a result, we do not perceive all regular objects colliding owing to mutual pulls. Because of their reciprocal gravitational pulls, the friction forces between the friends and the earth keep them from colliding.
(ix) Distinguish between:
(A) Real and pseudo forces,
| Real force | Pseudo force |
| A real force has its origin in any of the four basic interactions between matter. | A pseudo force arises due to the acceleration of the observer’ s frame of
reference and not due to any of the four basic interactions between matter. |
| A real force on one body due to another body is always accompanied by an equal and opposite reaction on the other body. | Newton's third law of motion does not apply in that there is no reaction force on some other body. |
(B) Conservative and non-conservative forces.
| Conservative force | Non-conservative force |
| The force required to move a body from one point to another is called a conservative force if the work done in moving the body between these points is independent of the path taken. | A force that is not conservative is called a non-conservative force. It is a dissipative path dependent force. |
| The work done on a body against a conservative force is stored in the body as its potential energy. | The work done against a non-conservative force is lost and cannot be converted into useful work later. |
| The work done on a body by a conservative force decrease the potential energy of the body, but the total mechanical energy of the body is conserved. | The work done on a body by a non-conservative force changes (decreases) the total mechanical energy of the body, i.e., the total mechanical energy is not conserved. |
(C) Contact and non-contact forces,
| Contact force | Non-contact force |
| A contact force arises due to direct physical contact between interacting objects. | A non-contact force acts without the necessity of physical contact between interacting objects. |
| A contact force has its origin in electro-magnetic interaction between the objects. | Each of the four fundamental forces of nature are non-contact action-at-a-distance type force. |
(D) Inertial and non-inertial frames of reference.
| Inertial frames | Non-inertial frames |
| A frame of reference in which every free body moves with a constant velocity (including zero) is called an inertial frame of reference. It is taken to be a frame fixed to the fixed distant stars.
A frame of reference which itself has uniform motion in a straight line with respect to an inertial frame of reference is also an inertial frame. |
An accelerated frame of reference, that is, one which has an acceleration with respect to an inertial frame of reference, is called a non-inertial frame of reference. |
| Newton's laws are obeyed in an inertial frame. | Newton's laws are not obeyed in a noninertial frame. |
| In this frame, any force acting on a body is a real force. | The acceleration of the frame gives rise to a pseudo force. |
(x) State the formula for calculating work done by a force. Are there any conditions or limitations in using it directly? If so, state those clearly. Is there any mathematical way out for it? Explain.
(a) The work done by a force in moving a body is defined to be the scalar product of the force and the displacement of the body.
Let be the force at a point along the path, and let θ be the angle between and at this point. Then, the work done during the displacement is
dW = (F cos θ) ds = \(\vec{F}.\vec{ds}\)
Then, W = \(\int_A^B{dW} = \int_A^B \vec{F}.\vec{ds}\)
This is the formula for calculating work done by variable force.
(b) The formula W = (\vec{F}.\vec{s}\) = (F cos θ)s is applicable only if (\vec{F}\) is constant, both in magnitude and direction, over the displacement
If the force varies in magnitude and/or direction, then we must consider dW = \(\vec{F}.\vec{ds}\) during an infinitesimal displacement \(\vec{ds}\) in an infinitesimal time interval dt→0. The total work done by the variable force in moving the body from point A to point B is given by the integrating dW over the path from A to B.
W = \(\int_A^B{dW} = \int_A^B \vec{F}.\vec{ds}\)
(c) Graphically, we plot the component of \(\vec{F}\) parallel to the direction of the motion at a point as a function of the displacement. Then, the total work is given by the area under the curve between the initial and final points.
(xi) Justify the statement, “Work and energy are the two sides of a coin”.
Work is considered to be done when a body moves in response to an external force.
The effect of another body or bodies is referred to as external force. Thus, if body 2 executes work on body 1, body 2 transfers energy to body 1, whose change in kinetic energy is equal to the work done on it according to the work-energy theorem. As a result, work and energy are considered to be two sides of the same coin.
(xii) From the terrace of a building of height H, you dropped a ball of mass m. It reached the ground with speed v. Is the relation _mgH = ½ mv2 applicable exactly? If not, how can you account for the difference? Will the ball bounce to the same height from where it was dropped?
- Let the ball dropped from the terrace of a building of height h have mass m. during free fail, the ball is acted upon by gravity (accelerating conservative force).
- While coming down, the work that is done is equal to the decrease in potential energy.
- This work done however is not entirely converted into kinetic energy but some part of it is used in overcoming the air resistance (retarding non-conservative force). This part of energy appears in some other forms such as heat, sound, etc.
- Thus, in this case of an accelerating conservative force along with a retarding non—conservative force, the work—energy theorem is given as, Decrease in the gravitational, PE. = increase in the kinetic energy + work done against non-conservative forces
- Thus, the relation mgh = ½ mv2 is not applicable when non-conservative forces are considered. The part of the energy converted to heat, sound, etc. also needs to be added to the equation.
- The ball will not bounce to the same height from where it was dropped due to the loss in kinetic energy during the collision making it an inelastic collision.
(xiii) State the law of conservation of linear momentum. It is a consequence of which law? Given an example from our daily life for conservation of momentum. Does it hold good during burst of a cracker?
Principle or law of conservation of linear momentum : When the resultant external force acting on a system is zero, the total linear momentum of the system is constant i.e., it is conserved. OR The total linear momentum of an isolated system, i.e., a system subject only to internal forces, is constant i.e., it is conserved.
The principle is a consequence of Newton's third law of motion.
Examples :
- As a person jumps out of a stationary boat, the boat moves in the backward direction. Initially, the momentum of the system was zero because both of them were at rest. While jumping, the forward momentum of the person must be equal in magnitude to the backward momentum of the boat such that their sum is zero and the total linear momentum of the person and boat is conserved.
- When a bomb explodes in mid-air, the fragments fly off in different directions However, it is found that the vector sum of the momenta of all the fragments at any instant always remains equal to the initial momentum of the bomb in both magnitude and direction. Here, there is an increase in KE and production of heat, sound and light because the chemical PE of its explosive ingredients is partly converted to these forms.
Linear momentum conservation during the burst of a cracker:
- The law of conservation of linear momentum holds good during the bursting of a cracker.
- When a cracker is at rest before the explosion, the linear momentum of the cracker is zero.
- When the cracker explodes into number of pieces, scattered in different directions, the vector sum of the linear momentum of these pieces is also zero. This is as per the law of conservation of linear momentum.
(xiv) Define coefficient of restitution and obtain its value for an elastic collision and a perfectly inelastic collision.
Coefficient of Restitution e: When two bodies collide with each other, the negative ratio of their relative velocity after collision to their relative velocity before collision, is called the coefficient of restitution (e).
Coefficient of restitution during a head-on, elastic collision:
Consider the head-on collision of two particles of masses m1 and m2, moving before the collision with constant velocities \(\vec{u_1}\) and \(\vec{u_2}\) in the laboratory frame of reference, see below Fig. After the collision they have velocities \(\vec{v_1}\) and \(\vec{v_2}\), again considered to be constant.
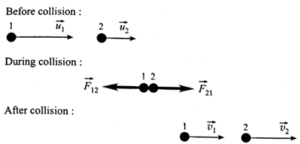
Since the collision is head-on, i.e., the motion is confined to one dimension, the velocity vectors all lie in the same line and hence we can write the equations in scalar form with the usual sign convention. Therefore, by the principle of conservation of linear momentum,
m1u1 + m2u2 = m1v1 + m2v2
or m1(u1 − v1) = m2(v2 − u2) …..(2)
Also, since the collision is elastic, total kinetic energy before collision = total kinetic energy after collision :
½ m1u12 + ½ m2u22 = ½ m1v12 + ½ m2v22
∴ m1(u12 − v12)=m2(v22 − u22)
Or m1(u1 − v1) (u1 + v1) = m2(v2 − u2) (v2 + u2) …….(3)
Dividing Eq. (3) by Eq. (2 ), we get,
u1 + v1 = v2 + u2 …….(4)
Rearranging the terms in Eq. (4),
u1 − u2 = v2 − v1 …….(5)
Here, (u1 − u2) is the velocity with which particle 1 approaches particle 2 before collision and (v2 − v1) is the velocity with which particle 2 separates away from particle 1 after collision.
Hence, in a head-on elastic collision, velocity of separation = velocity of approach.
From Eq. (5), the coefficient of restitution,
e = \(\frac{v_2-v_1}{u_1-u_2}\) = 1
In a perfectly inelastic collision, the colliding particles stick together and move with a common velocity. That is, their velocity of separation after the collision is zero. Therefore, the coefficient of restitution,
e = \(\frac{\text{velocity of separation}}{\text{velocity of approach}}\) = 0
Thus, for an elastic collision, coefficient of restitution, e =1. For a perfectly inelastic collision, e =0 (by definition). Thus, for any collision, the coefficient of restitution lies between 1 and 0.
(xv) Discuss the following as special cases of elastic collisions and obtain their exact or approximate final velocities in terms of their initial velocities.
(a) Colliding bodies are identical.
(b) A very heavy object collides on a lighter object, initially at rest.
(c) A very light object collides on a comparatively much massive object, initially at rest.
Two particles of masses m1 and m2 move with initial velocities u1 and u2 such that particle 1 collides head-on elastically with particle 2.
Their respective velocities after the collision are
v1 = \((\frac{m_1-m_2}{m_1+m_2})u_1+(\frac{2m_2}{m_1+m_2})u_2\)
v2 = \((\frac{2m_1}{m_1+m_2})u_1+(\frac{m_2-m_1}{m_1+m_2})u_2\)
Special cases :
(a) If the Colliding bodies are identical (or equal masses), m1 = m2
Substituting m1 = m2 in the above equations,
v1 = \((0)u_1+(\frac{2m_2}{2m_2})u_2\) = u2
and v2 = \((\frac{2m_1}{2m_1})u_1+(0)u_2\) = u1
This shows that in a head-on elastic collision of two particles of equal masses, the particles exchange their velocities.
Further, if the second particle is at rest before the collision, u2 = 0, so that after the collision, v1 = 0 and v2 = u1 that is, the first particle initially moving stops and the second one takes off with the initial velocity of the first.
(b) If colliding body is much heavier and the struck body is initially at rest, i.e., m1 >> m2 and u2= 0
Then,
v1 ≅ \((\frac{m_1}{m_1})u_1\) ≅ u1
and v2 ≅ \((\frac{2m_1}{m_1})u_1\) ≅ 2u1
that is, if a massive particle makes an elastic head-on collision with a light one at rest, the massive one continues its motion at almost the same speed, and the light one takes off at nearly twice this speed.
(c) The body which is struck is much heavier than the colliding body and is initially at rest, i.e., m1 << m2 and u2= 0
Then, ignoring m1 in comparison to m2, the final velocities are
v1 ≅ \((-\frac{m_1}{m_1})u_1\) ≅ −u1 and v2 ≅ (0)u1 ≅ 0
Thus, if a light particle makes an elastic collision with a massive one at rest, it rebounds with almost its initial speed; the massive one is almost unaffected.
(xvi) A bullet of mass m1 travelling with a velocity u strikes a stationary wooden block of mass m2 and gets embedded into it. Determine the expression for loss in the kinetic energy of the system. Is this violating the principle of conservation of energy? If not, how can you account for this loss?
Consider a perfectly inelastic, head on collision of two bodies of masses m1 and m2 with respective initial velocities u1 and u2. As the collision is perfectly inelastic, they move jointly after the collision, i.e., their final velocity is the same. Let it be v.
According to conservation of linear momentum,
m1u1 + m2u2 = (m1 + m2)v
∴ v = \(\frac{m_1u_1+m_2u_2}{m_1+m_2}\)
This is the common velocity after a perfectly inelastic collision
Loss in the kinetic energy :
Loss in K.E. = Δ (K.E.) = Total initial K.E. − Total final K.E.
= ½ (m1+m2)v2 – (½ m1u12 + ½ m2u22)
= ½ (m1+m2)\((\frac{m_1u_1+m_2u_2}{m_1+M-2})^2\) – (½ m1u12 + ½ m2u22)
= \(\frac{1}{2}[\frac{(m_1u_1+m_2u_2)^2}{m_1+m_2}-(m_1u_1^2+m_2u_2^2)]\)
= \(\frac{1}{2}[\frac{m_1u_1^2+2m_1m_2u_1u_2+m_2^2u_2^2-m_1^2u_1^2-m_2^2u_2^2-m_1m_2u_1^2-m_1m_2u_2^2}{m_1+m_2}]\)
= \(\frac{1}{2}[-\frac{m_1m_2(u_1^2+u_2^2-2u_1u_2)}{m_1+m_2}]\) = \(-\frac{1}{2}(\frac{m_1m_2}{m_1+m_2})(u_1-u_2)^2\)
Since the bracketed terms are always positive, the minus sign in Eq. (2) shows that the final kinetic energy is less than the initial kinetic energy. That is, there is a loss in kinetic energy.
∴ Loss in KE = initial KE — final KE = \(\frac{1}{2}(\frac{m_1m_2}{m_1+m_2})(u_1-u_2)^2\)
The loss in KE of the bullet is partly utilised in doing work against the retarding force of the block, partly in deforming the wood, and the rest is converted into heat and vibrational energy. Total energy is conserved, and the principle of energy conservation is not violated.
(xvii) One of the effects of a force is to change the momentum. Define the quantity related to this and explain it for a variable force. Usually when do we define it instead of using the force?
(a) For a force \(vec{F}\) which is constant over the time interval Δt during which it acts, the impulse of the force is defined as the product \(\vec{F}\)Δt :
\(\vec{J}\) = \(\vec{F}\)Δt
Newton's second law of motion, which duplicates the first law with quantitative precision, states that the change in momentum of a body equals the impulse of the applied force and is made in the direction of that force.
Then,
\(\vec{J}=\vec{dp}=\vec{p_f}-\vec{p_i}=m(\vec{v}-\vec{u})\)
where m is the mass of the body \(\vec{p_i}\) and \(\vec{p_f}\) are the initial and final momenta of the body over the time interval of the impulse.
For a time-varying force \(\vec{F}(t)\), whose magnitude over the interval Δt is given by the curve in Fig. (a), the impulse of the force is given by the area under the curve :
\(\vec{J}=\int_{t_i}^{t_f}\vec{F}dt\)

For a time-varying force, the magnitude of the impulse can also be written as
J = Fav Δt
where Fav is the average force that would impart the same impulse as the variable force over the time interval, i.e., the area Fav Δt of the rectangle in Fig. (b) is equal to the area under the curve in Fig. (a).
(b) Force is an abstract concept while what we actually observe is the change in momentum. The concept of impulse becomes more useful when the force varies with time, as in a two-body collision.
(xviii) While rotating an object or while opening a door or a water tap we apply a force or forces.
(a) Under which conditions is this process easy for us? Why?
(b) Define the vector quantity concerned.
(c) How does it differ for a single force and for two opposite forces with different lines of action?
(a)

- While opening a door fixed to a frame on hinges, turning a door requires the least force when it is applied as far away from the rotation axis of the hinges as possible. So, handles on doors are put as far away as possible from the hinges.
- Also, it is easier to turn a door if the force is applied perpendicular to the rotation axis.
- Thus, turning effect of a force or torque depends on the magnitude of the force, its direction and point of application.
- For a measure of the turning effect of a force lying in a plane perpendicular to the axis of rotation, we must consider the magnitude of the applied force and the distance of its line of action from the axis.
(b) Torque or moment of a force about a point : The moment of a force about a point or torque is a quantitative measure of the ability of a force to change the state of rotation of a body. The magnitude of the torque is the product of the magnitude of the force and the moment arm.
Consider a rigid body free to rotate about an axis as shown (Fig). Suppose a force \(\vec{F}\) acts on the body at point P. The position vector of the point of application of the force with respect to the axis is \(\vec{r}\)
The moment arm of the force is the perpendicular distance rL from the axis to the line of action of the force. If θ is the smaller angle between \(\vec{r}\) and \(\vec{F}\), rL = r sin θ.
The magnitude of the torque is τ = FrL = Fr sin θ = rF sin θ
The rotation of a body about a single axis would be clockwise or anticlockwise. The torque is considered positive if it tends to rotate the body anticlockwise, and is negative if it tends to rotate the body clockwise.
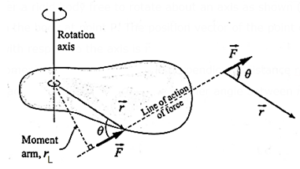
In vector form,
\(\vec{τ}\) = \(\vec{r}×\vec{F}\)
The direction of \(\vec{τ}\) is thus given by the right-handed screw rule for a vector product.
(c) Distinguish between the torques of a force and a couple :
In many situations the word couple is used synonymous to moment of the couple or its torque, i.e., every time we may not say it as torque due to the couple, but say that a couple is acting. (***write any two points)
| Torques of a force (Moment of a force ) | Torques of a couple (Moment of a couple) |
| \(\vec{τ}\) = \(\vec{r}×\vec{F}\) | \(\vec{τ}\) = \(\vec{r_{12}}×\vec{F_1}\) = \(\vec{r_{21}}×\vec{F_2}\) |
| \(\vec{τ}\) depends upon the axis of rotation and the point of application of the force. | \(\vec{τ}\) depends only upon the two forces, i.e., it is independent of the axis of rotation or the points of application of forces. |
| It can produce translational acceleration also, if the axis of rotation is not fixed or if friction is not enough. | Does not produce any translational acceleration, but produces only rotational or angular acceleration. |
| Its rotational effect can be balanced by a proper single force or by a proper couple. | Its rotational effect can be balanced only by another couple of equal and opposite torque. |
(xix) Why is the moment of a couple independent of the axis of rotation even if the axis is fixed?
Let a couple of a pair of forces \(\vec{F_1}\) and \(\vec{F_2}\) in the plane of the page act on the rigid body as shown (Fig.). \(\vec{F_2}\) = \(-\vec{F_1}\) Let F1 = F2 = F. The perpendicular distance rL = AB is the arm of the couple.
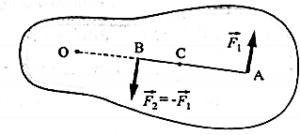
(1) About the point O :
The torque due to \(\vec{F_1}\);
\(\vec{τ_1}\) = \(\vec{OA}×\vec{F_1}\)
∴ τ 1 = F(OA) (anticlockwise)
The torque due to \(\vec{F_2}\) is
\(\vec{τ_2}\) = \(\vec{OB}×\vec{F_2}\)
∴ τ 2 = −F(OB) (clockwise)
Since the torques obey the superposition principle of forces, the resultant torque on the body is the sum \(\vec{τ_1}\) of \(\vec{τ_2}\) and
τ = τ 1 + τ 2 = F(OA) − F(OB)
= F(OA − OB) = F(AB) = FrL (anticlockwise) …..(1)
(2) About the point C :
τ 1 = F(CA) and τ 2 = F(CB) (both anticlockwise)
τ = τ 1 + τ 2 = F(CA) + F(CB)
= F(AB) = FrL (anticlockwise) ……(2)
From Eqs. (1) and (2), the torque due to a couple about any point in its plane is the same, i.e., it is independent of the axis of rotation.
(xx) Explain balancing or mechanical equilibrium. Linear velocity of a rotating fan as a whole is generally zero. Is it in mechanical equilibrium? Justify your answer.
Balancing or mechanical equilibrium :
The momentum of a system is constant in the absence of an external unbalanced force. This state is called mechanical equilibrium.
- A rigid body is said to be in equilibrium if there is no change in its state of motion.
- If there is no change in its velocity, the body is said to be in translational equilibrium.
- If there is no change in the rotational state of the body, it is said to be in rotational equilibrium.
Condition for translational equilibrium:
A rigid body is in translational equilibrium when the resultant force acting on it is zero. By Newton's first law of motion, a body remains in its natural state of constant velocity (including zero) if the net force on the body is zero.
For translational equilibrium, the forces acting on the body must be concurrent. Thus, if F1, F2, F3,.. are concurrent forces acting on a rigid body the first condition of equilibrium is
\(\vec{F_1}+\vec{F_2}+\vec{F_3}\) = 0 or ∑ \(\vec{F_i}\) = 0
Condition for rotational equilibrium : A rigid body is in rotational equilibrium when the resultant torque acting on it is zero. If the forces acting on a rigid body are not concurrent, then their resultant may form a couple. Since the sum of the forces constituting a couple is zero, the first condition for equilibrium is satisfied, But the action of the couple is to change the state of rotation of the body. A body at rest will start rotating, or if it was initially rotating, it will speed up or slow down.
Thus, if \(\vec{F_1}\), \(\vec{F_2}\), \(\vec{F_3}\) ,.. are nonconcurrent forces acting on a rigid body and \(\vec{τ_1}\), \(\vec{τ_2}\), \(\vec{τ_3}\), are the respective torques produced by them about any point, the second condition for equilibrium is
\(\vec{τ_1}\) + \(\vec{τ_2}\) + \(\vec{τ_3}\)…. = 0 or ∑ \(\vec{τ_i}\) = 0
Rotating fan in mechanical equilibrium :
- When a ceiling/table fan is stationary, it satisfies the condition for translational equilibrium.
- When the blades of the fan rotate with constant angular velocity, their angular acceleration is zero. Hence, it also satisfies the condition for rotational equilibrium. Therefore, a fan rotating with constant angular velocity is in mechanical equilibrium.
(xxi) Why do we need to know the centre of mass of an object? For which objects, its position may differ from that of the centre of gravity?
In real life, we always come across finite objects (objects of measurable sizes). Concept of centre of mass helps us in considering these objects to be point objects at a particular location, thereby allowing us to apply Newton’s laws of motion.
The centre of gravity of a body does not coincide with its centre of mass when the body is in a nonuniform gravitational field or, equivalently, when the extent of the body is very large.
Question 3.
Solve the following problems.
(i) A truck of mass 5 ton is travelling on a horizontal road with 36 km/hr stops on traveling 1 km after its engine fails suddenly. What fraction of its weight is the frictional force exerted by the road? If we assume that the story repeats for a car of mass 1 ton i.e., can moving with same speed stops in similar distance same how much will the fraction be?
Given : m = 5 ton = 5000 kg, u = 36 km/h = 36000 m/3600 s = 10 m/s, v = 0,
s = 1 km = 1000 m, g = 10 m/s2
v2 − u2 = 2as ∴ 0 − u2 = 2as
∴ a = \(-\frac{u^2}{2s}\) = \(-\frac{10^2}{2×1000}\) = \(-\frac{100}{2000}\)
= \(-\frac{1}{20}\) m/s2
The frictional force exerted by the road on the truck = |ma|
\(\frac{|ma|}{|mg|}\) = \(\frac{|a|}{|g|}\) = \(\frac{1/20}{10}\) = \(\frac{1}{200}\)
This gives the required fraction. It has the same value for the truck and the car.
(ii) A lighter object A and a heavier object B are initially at rest. Both are imparted the same linear momentum. Which will start with greater kinetic energy: A or B or both will start with the same energy?
Let m1 and m2 be me masses of lighy object A and heavy objects B and v1 and v2 be their respective velocities.
Since both are imparted with the same linear momentum,
m1 v1 = m2 v2
The kinetic energy of the lghter object A
K.E.A = \(\frac{1}{2}\)m1 v12
The kinetic energy of the heavier object B
K.E.B = \(\frac{1}{2}\)m2 v22
…(‘.’ m1 v1 = m2 v2)
m1.K.E.A = m2.K.E.B
As m1 < m2 therefore K.E.A > K.E.B lighter object A has more kinetic energy.
(iii) As I was standing on a weighing machine inside a lift it recorded 50 kg wt. Suddenly for few seconds it recorded 45 kg wt. What must have happened during that time? Explain with complete numerical analysis.
Given : mg = 50 kg wt, mg − ma =45 kg wt as the reading recorded by the weighing machine is less than mg, g = 10 m/s2
∴ \(\frac{mg-ma}{mg}\) = \(\frac{45}{50}\)
∴ \(1-\frac{a}{g}=\frac{9}{10}\)
∴ \(\frac{a}{g}=1-\frac{9}{10}=\frac{1}{10}\)
∴ a = g/10 = 10/10 = 1 m/s2
The lift must be coming down with this acceleration.
(iv) Figure below shows a block of mass 35 kg resting on a table. The table is so rough that it offers a self adjusting resistive force 10% of the weight of the block for its sliding motion along the table. A 20 kg wt load is attached to the block and is passed over a pulley to hang freely on the left side. On the right side there is a 2 kg wt pan attached to the block and hung freely. Weights of 1 kg wt each, can be added to the pan. Minimum how many and maximum how many such weights can be added into the pan so that the block does not slide along the table?
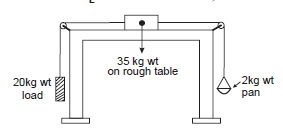
Let mB and mL be the masses of the block and the hanging load, respectively. Let mo be the mass of the pan and m1 the mass added to the pan. Let fs be the friction (self-adjusting resistive) force on the block.
Given : mB = 35 kg, mL = 20 kg, mo = 2 kg, f= 10% of mBg = 0.1mBg
The total mass on the right hand side is
m = mo + m1

From the free-body diagrams for the hanging load and the pan, shown in Figs. 4.7 (a) and (b), for the system to be at rest,
T1 − mLg = 0 T1 = mLg ……(1)
and T2 — mg = 0 T2 = mg ……..(2)
If the total mass on the right hand side, m, is less than a certain minimum, the block will tend to slide to the left, so that fs will be to the right, Fig. (c). Then,
T1 − T2 − fS = mBa (a is to the left)
mLg – mg − fS = mBa …....(3)
If m is more than a certain maximum, the block will tend to slide to the right, so that fs will be to the left, Fig. (d). Then,
T2 − T1 − fs = mBa (a is to the left)
mg − mLg − fs = mBa …...(4)
For the block to be at rest, i.e., a = 0, Eqs. (3) and (4) respectively sets the minimum and maximum values of m.
From Eq. (3),
(mL − m − 0.1mB) g = 0
∴ m = mL − 0.1mB = [20 − 0.1(35)]kg
mo + m1 = 20 − 3.5 = 16.5 kg
m1 = 16.5 kg − mo = 16.5 − 2 = 14.5 kg
Hence, minimum 15 weights, each of 1 kg wt, can be added to the pan.
From Eq. (4),
(m − mL − 0.1mB) g = 0
m = mL + 0.1mB = [20 + 0.1(35)]kg
mo + m1 = 20 + 3.5 = 23.5 kg
m1 = 23.5 kg − mo = 23.5 − 2 = 21.5 kg
Hence, maximum 21 weights, each of 1 kg wt, can be added to the pan.
(v) Power is rate of doing work or the rate at which energy is supplied to the system. A constant force F is applied to a body of mass m. Power delivered by the force at time t from the start is proportional to
(a) t (b) t2 (c) (d) t0
Derive the expression for power in terms of F, m and t.
The power P delivered by a force is the time rate of work done by the force :
P = dW/dt
Under the action of a constant force if the displacement of the body in an infinitesimal time interval dt is , the infinitesimal work done by the force in this time dt is
dW = \(\vec{F}\vec{ds}\)
∴ P = \(\vec{F}\frac{\vec{ds}}{dt}\) = \(\vec{F}.\vec{v}\) = Fv cos θ
Since \(\vec{F}\) is constant, the acceleration \(\vec{a}=\frac{\vec{F}}{m}\) is also constant.
∴ \(\vec{u}=\vec{u}+\vec{a}t=\vec{a}t\) ('.'u = 0)
∴ \(\vec{u}\) = \(\frac{\vec{F}}{m}t\) = \(\frac{F^2t}{m}\)
∴ P = \(\vec{F}.\frac{\vec{F}}{m}t\) is the required expression
. ∴ P ∝ t
(vi) 40000 litre of oil of density 0.9 g cc is pumped from an oil tanker ship into a storage tank at 10 m higher level than the ship in half an hour. What should be the power of the pump?
Given : V = 40000, L = 40 m3, ρ = 0.9 g/cm3 = 900 kg/m3, h = 10 m,
g = 10 m/s2, t = 30 min = 1800 s
The power of the pump, P = work done/tlme
∴ P = \(\frac{mgh}{t}\) = \(\frac{(Vρ)gh}{t}\)
= \(\frac{40×900×10×10}{1800}\)
= 20 x 100 = 2000 W = 2kW
(vii) Ten identical masses (m each) are connected one below the other with 10 strings. Holding the topmost string, the system is accelerated upwards with acceleration g/2. What is the tension in the 6th string from the top (Topmost string being the first string)?
For the mass at the top see below Fig.,

T1 − (T2 + mg) = ma (upward) .... (1)
For the subsequent masses,
T2 − (T3 + mg) = ma ……(2)
T3 − (T4 + mg) = ma …..(3)
T4 − (T5 + mg) = ma …..(4)
T5 − (T6 + mg) = ma ……(5)
Adding all these equations, we get,
T1 − T6 − 5mg = 5ma
T6 = T1 − 5 mg − 5ma
Now, T1 − 10 mg = 10 ma
.'.T1 = 10 mg + 10 ma
.'. T6 = 10mg + 10ma − 5mg − 5ma
.'.T6 = 5mg + 5ma = 5m(g+a)
Now, a = g/2
The tension in the 6th string,
T6 = 5m(g + \(\frac{g}{2}\)) = 5m\((\frac{3g}{2})\) = \(\frac{15}{2}\)mg
= 7.5 mg
[Note : If we take a = 0.2g, then T6 = 5mg + 5m(0.2g) =5mg + mg = 6mg which is the answer given in the textbook]
(viii) Two galaxies of masses 9 billion solar mass and 4 billion solar mass are 5 million light years apart. If, the Sun has to cross the line joining them, without being attracted by either of them, through what point it should pass?
Data: r = rA + rB = 5 x 106 ly
mA = 9 x 109 Ms, mB = 4 x 109 Ms
Ms = solar mass
For the net gravitational force on the Sun due to the two galaxies to be zero, the path of the Sun must be perpendicular to the line joining the two galaxies. Let rA and rB be the distances of the galaxies A and B from the Sun as it crosses the line joining the galaxies. At this point, the magnitudes of the gravitational force on the Sun due to the galaxies A and B are, respectively,
FSA = \(\frac{Gm_AM_S}{r^2_A}\) and FSB = \(\frac{Gm_BM_S}{r^2_B}\)
Since, FSA = FSB
\(\frac{m_A}{r^2_A}=\frac{m_B}{r^2_B}\)
∴ \(\frac{r^2_A}{r^2_B}=\frac{m_A}{m_B}\) = \(\frac{9×10^9}{4×10^9}\) = \(\frac{9}{4}\)
∴ \(\frac{r_A}{r_B}=\frac{3}{2}\)
∴ rA = \(\frac{3}{2}\)rB
∴ rA + rB = 5 x 106 ly
∴ \(\frac{3}{2}\)rB + rB = 5 x 106 ly
∴ \(\frac{5}{2}\)rB = 5 x 106 ly
∴ rB = 2 x 106 ly and rA = 3 x 106 ly
The neutral point on the line joining the two galaxies, where the sun experiences no net force due to the galaxies, is 3 million light years from the 9 billion solar massive galaxy.
(ix) While decreasing linearly from 5 N to 3 N, a force displaces an object from 3 m to 5 m. Calculate the work done by this force during this displacement.
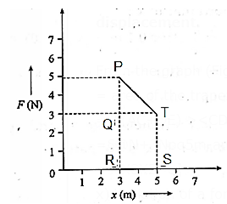
From the graph (Fig.), the work done by the linearly varying force
= area of the trapezium PRST
= \(\frac{1}{2}\)(PR+ST) x RS
= \(\frac{1}{2}\)(5N + 3N) x (5m − 3m)
= \(\frac{1}{2}\) x 8 x 2 = 8 J
(x) Variation of a force in a certain region is given by F = 6x2 − 4x − 8. It displaces an object from x = 1 m to x = 2 m in this region. Calculate the amount of work done.
Given : F = (6x2 − 4x − 8)N, xi = 1 m, xf=2 m
The work done by the force,
W = \(\int_{x_i}^{x_f} Fdx = \int_{x_i}^{x_f}(6x^2-4x-8)dx\)
= \([6(\frac{x^3}{3})-4(\frac{x^2}{2})-8x]-{x_i=1}^{x_i=2}\)
= \([2x^3 − 2x^2 −8x]_1^2\)
=(2 x 8 − 2 x 4 − 8 x 2) − (2 – 2 − 8)
=(16 – 8 −16) − (−8)
= −8 + 8 = 0 J
(xi) A ball of mass 100 g dropped on the ground from 5 m bounces repeatedly. During every bounce 64% of the potential energy is converted into kinetic energy. Calculate the following:
(a) Coefficient of restitution.
(b) Speed with which the ball comes up from the ground after third bounce.
(c) Impulse given by the ball to the ground during this bounce.
(d) Average force exerted by the ground if this impact lasts for 250 ms.
(e) Average pressure exerted by the ball on the ground during this impact if contact area of the ball is 0.5 cm2.
Given: m = 100 g = 0.1 kg, g = 10 m/s2, h=5 m, conversion of 64% of PE into KE during every bounce, t = 250 ms = 0.25 s, A = 0.5 cm2 = 0.5 x 10-4 m2
(a) Just before the ball strikes the ground for the first time, \(\frac{1}{2}\)mv12 = mgh
Just after the first bounce, \(\frac{1}{2}\)mv22 = 0.64 mgh
∴ \(\frac{v_2^2}{v_1^2}\) = 0.64
∴ \(\frac{v_2}{v_1}\) = 0.8
The coefficient of restitution
e = [velocity of separation]/[velocity of approach] = \(\frac{v_2}{v_1}\) = 0.8
(b) Initial PE = mgh = 0.1 x 10 x 5 = 5 J
After the first bounce,
KE = 0.64 x 5 J
After the second bounce,
KE = 0.64 x 0.64 x 5 J
After the third bounce,
KE = 0.64 x 0.64 x 0.64 x 5 J
= (0.64)3 x 5 J
If v is the corresponding speed of the ball,
\(\frac{1}{2}\)mv2 = (0.64)3 x 5
mv2 = (0.64)3 x 10
Now, m = 0.1 kg ∴ 0.1 v2 = (0.64)3 x 10
∴ v2 = (0.64)3 x 100
∴ v = (0.64)3/2 x 10 = [(0.64)1/2]3 x 10
= 10 x (0.8)3 = 10 x \(\frac{512}{1000}\) = 5.12 m/s
(c) After the second bounce \(\frac{1}{2}\)mv22 = 0.64 x 0.64 x 5 J
∴ \(\frac{1}{2}\) x 0.1 v2 = (0.64)2 x 5
∴ v2 = (0.64)2 x 10 x 10
v = 0.64 x 10 = 6.4 m/S
Impulse = change in momentum
= 0.1 x 6.4 kg.m/s − (− 0.1 x 5.12 kg.m/s)
(considering the direction of the velocity)
= 0.1 x (6.4 + 5.12) = 0.1 x 11.52
= 1.152 kg.m/s
= 1.152 N.S
(d) Impulse \(\vec{F}\)t = 1.152 N.s, t = 0.25 s
∴ Average force, \(\vec{F}\) = \(\frac{1.152}{0.25}\) = 4 x 1.152
∴ = 4.608 N
(e) Average pressure = \(\frac{\vec{F}}{A}\) = \(\frac{4.608}{0.5×10^4}\)
= 2 x 4.608 x 104
= 9.216 x 104 N/m2
= 9.216 x 104 Pa
(xii) A spring ball of mass 0.5 kg is dropped from some height. On falling freely for 10 s, it explodes into two fragments of mass ratio 1:2. The lighter fragment continues to travel downwards with speed of 60 m/s. Calculate the kinetic energy supplied during explosion.
Given : m = 0.5 kg, g = 10 m/s2, free fall for 10 S, \(\frac{m_1}{m_2}\) = \(\frac{1}{2}\) , m1 + m2 = 0.5 kg, v of m1 = 60 m/s
∴ m1 = \(\frac{m_2}{2}\)
Also, m1 + m2= 0.5 kg
∴ \(\frac{m_2}{2}\) + m2 = 0.5
∴ \(\frac{3}{2}\)m2 = 0.5 = \(\frac{1}{2}\) ∴ m2 = \(\frac{1}{3}\) kg
∴ m1 = \(\frac{m_2}{2}\) = \(\frac{1}{6}\)kg
Free fall of m : v = gt = 10 x 10 = 100 m/s
The corresponding KE of m = \(\frac{1}{2}\)mv2
= \(\frac{1}{2}\) x 0.5 x (100)2 = 2500 J
KE of m1 = \(\frac{1}{2}\)m1v12 = \(\frac{1}{2}×\frac{1}{6}×(60)^2\) = 300 J
By momentum conservation,
mv = m1v1 + m2v2
∴ 0.5 x 100 = \(\frac{1}{6}×60+\frac{1}{3}v_2\) = 10 + \(\frac{v_2}{3}\)
∴ \(\frac{v_2}{3}\) = 50 − 10 = 40
∴ v2 = 120 m/s
KE of m2 = \(\frac{1}{2}\)m2v22 = \(\frac{1}{2}×\frac{1}{3}×(120)^2\) = 2400 J
Total KE of the fragments = 300 + 2400
= 2700 J
KE of the ball just before the explosion = 2500 J
Hence, the KE supplied during the explosion = 2700 J — 2500 J = 200 J
(xiii) A marble of mass 2m travelling at 6 cm/s is directly followed by another marble of mass m with double speed. After collision, the heavier one travels with the average initial speed of the two. Calculate the coefficient of restitution.
Mass of marble 1 m1 = m, u1 = 12 cm/s,
Mass of marble 2 m2 = 2m, u2 = 6 cm/s,
After collision speed of m2 = average speed of two = (12+6)/2 = 9 cm/s = v2
By momentum conservation,
m1u1 + m2u2 = m1v1 + m2v2
∴ mu1 + 2mu2 = mv1 + 2mv2 (..m1 = m, m2 = 2m)
∴ 12m + 12m = mv1 + 18 m (..u1 = 12, u2 = 6)
∴ v1 = 24 − 18 = 6 cm/s
v2 − v1 = 9 − 6 = 3 cm/s
u1 − u2 = 12 − 6 = 6 cm/s
The coefficient of restitution,
e = \(\frac{v_2-v_1}{u_1-u_2}=\frac{3}{6}\) = 0.5
(xiv) A, 2 m long wooden plank of mass 20 kg is pivoted (supported from below) at 0.5 m from either end. A person of mass 40 kg starts walking from one of these pivots to the farther end. How far can the person walk before the plank topples?
Given : W = 20 kg, W1 = 40 kg
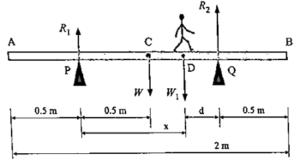
In Fig. AB = 2 m, AP = PC = CQ = QB = 0.5m,
Suppose the person starts walking from pivot P towards Q. Also, suppose the plank begins to topple when the person is at point D, a distance x from P. At that instant, the upward reaction R1 at P becomes zero.
Taking moments about pivot Q,
W x QC + W1 x QD + (−R2) x 0 = 0
∴ W1 x QD = −W x QC
∴ QD = (−W x QC)/W1 = −(20 x 0.5)/40 = − 0.25 m
|d| = 0.25 m
PD = x = PQ − |d| = 1 − 0.25 = 0.75 m
∴ The person can walk up to 0.75 m from pivot P, i.e., 1.25 m from end A.
(xv) A 2 m long ladder of mass 10 kg is kept against a wall such that its base is 1.2 m away from the wall. The wall is smooth but the ground is rough. Roughness of the ground is such that it offers a maximum horizontal resistive force (for sliding motion) half that of normal reaction at the point of contact. A monkey of mass 20 kg starts climbing the ladder. How far can it climb along the ladder? How much is the horizontal reaction at the wall?
Data : From Fig. Ladder AB = L = 2 m, W = 10 kg, OB = 1.2 m, W1 = 20 kg,
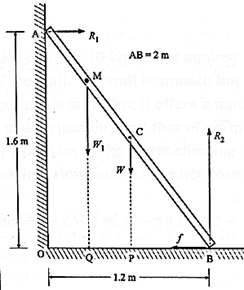
f = 0.5R2
Since Δ OAB is a right triangle, right-angled at O,
OA = \(\sqrt{AB^2-OB^2}\) = \(\sqrt{2^2-1.2^2}\)
= \(\sqrt{4-1.44}\) = = \(\sqrt{2.56}\) = 1.6 m
According to the first condition for equilibrium,
∑ Fy = 0 = R2 − W − W1 = 0 ……(1)
and ∑ Fx = 0 = R1 − f …..(2)
From Eq. (1),
R2 = W + W1 = 10 + 20 = 30 kg
From Eq. (2) and data,
R1 = f = 0.5 R2 = 0.5 (30) = 15 kg
The horizontal reaction at the wall,
R = 15 kg = 15 kg x 10 m/s2 = 150 N
From the second condition for equilibrium, taking moments about B,
—R1 x OA + W1 x BQ + W x BP + (R2) x 0 + (—f) x 0 = 0
∴ W1 x BQ = R1 x OA – W x BP
BP = \(\frac{1}{2}\)BE = \(\frac{1}{2}\)(1.2 m) = 0.6 m
∴ BQ = \(\frac{(15×1.6)-(10×0.6)}{20}\) = \(\frac{24-6}{20}\) = 0.9 m
BM/BA = BQ/BE
∴ BM = 2(\(\frac{0.9}{1.2})\) = 1.5 m
∴ The monkey can climb up 1.5 m along the ladder.
(xvi) Four uniform solid cubes of edges 10 cm, 20 cm, 30 cm and 40 cm are kept on the ground, touching each other in order. Locate centre of mass of their system.
Given : L1 = 10 cm, L2 = 20 cm, L3 = 30 cm, L4 = 40 cm.
L2/L1 = 20/10 = 2, ∴ (L2/L1)3 = 8
L3/L1 = 30/10 = 3, ∴ (L3/L1)3 = 27
L4/L1 = 40/10 = 4, ∴ (L3/L1)3 = 64
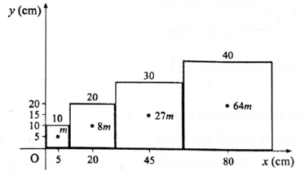
Mass = volume x density; volume = L3
Let m1= m = mass of cube A
Mass of cube B, m2 = 8m; mass of cube C, m3 = 27m; mass of cube D, m4 = 64m
∴ m1 + m2 + m3 + m4 = m + 8m + 27m + 64m = 100m
From the figure, x1 = 5 cm, x2 = 20 cm, x3 = 45 cm, x4 = 80 cm
∴ XCM = \(\frac{m_1x_1+m_2x_2+m_3x_3+m_4x_4}{m_1+m_2+m_3+m_4}\)
= \(\frac{m×5+8m×20+27m×45+64m×80}{100m}=\frac{6500m}{100m}\)= 65 cm
Also y1 = 5m, y2 = 10 cm, y3 = 15 cm, y4 = 20 cm
∴ YCM = \(\frac{\sum_im_iy_i}{\sum_im_i}\) = \(\frac{1×5+8×10+27×15+64×20}{100}=\frac{1770}{100}\) = 17.7 cm
Similarly z1 = 5 cm, z2 = 10 cm, z3 = 15 cm, z4 = 20 cm
∴ ZCM = 17.7 cm
(xvii) A uniform solid sphere of radius R has a hole of radius R/2 drilled inside it. One end of the hole is at the centre of the sphere while the other is at the boundary. Locate centre of mass of the remaining sphere.
Let M = mass of the sphere of radius R, ρ = density of the material of the sphere
ρ = mass/volume
∴ M = \((\frac{4}{3}πR^3)ρ\)
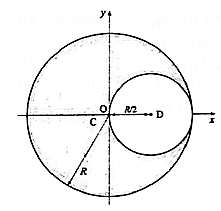
If we imagine the hole (spherical cavity) to be filled with the same material as that of the sphere, the mass of this (smaller) sphere
= \(\frac{4}{3}π(\frac{R}{2})^3ρ=\frac{M}{8}\)
M − M/8 = 7M/8
Treating the hole as a sphere with mass –M/8, the X coordinate of the centre of mass (C) of the remaining sphere will be
XCM = \(\frac{\sum_im_ix_i}{\sum_im_i}\) = \(\frac{0-(M/8)(R/2)}{7(M/8)}\)
= \(-\frac{R}{16}×\frac{8}{7}=-\frac{R}{14}\)
(xviii) In the following table, every item on the left side can match with any number of items on the right hand side. Select all those.
| Types of collision | Illustrations |
| (a) Elastic collision
(b) Inelastic collision (c) Perfectly inelastic collision (d) Head on collision |
(i) A ball hit by a bat.
(ii) Molecular collisions responsible for pressure exerted by a gas. (iii) A stationary marble A is hit by marble B and the marble B comes to rest. (iv) A blob of clay dropped on the ground sticks to the ground. (v) Out of anger, giving a kick to a wall. (vi) A striker hits the boundary of a carrom board in a direction perpendicular to the boundary and rebounds. |
(a) —(ii) : (b) -(i), (iii), (iv), (v), (vi) : (c) - (iii), (iv) : (d) - (iii), (iv).
Main Page : – Maharashtra Board Class 11th-Physics – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter 3: Motion in a Plane – Online Solutions
Next Chapter : Chapter 5: Gravitation – Online Solutions
We reply to valid query.