Notes-Class-10-Mathematics-1-Chapter-3-Arithmetic Progression-Maharashtra Board

Topics to be learn : Sequence nth term of an A.P. Arithmetic Progression Sum of n terms of an A.P.

Sequence :

A set of numbers where the numbers are arranged in a definite order according to some definite rule is called a sequence.

Examples :

(i) 1, 2, 3, 4, 5, are serial numbers in a set of natural numbers.

(ii) 1, 3, 5, 7, 9, are odd numbers in a set of natural numbers.

(iii) 1, 4, 9, 16, 25, are the squares of the serial numbers in a set of natural numbers.

• In each of the above arrangements, there is some relationship between any two consecutive numbers
• The numbers are denoted by a₁, a₂, a₃, ..., a_n. a₁ is the first term, a₂ is the second term, ..., a_n is the nth term
• The sequence of numbers is denoted by f₁, f₂, f₃,…… .

 Activity : Complete the given pattern :

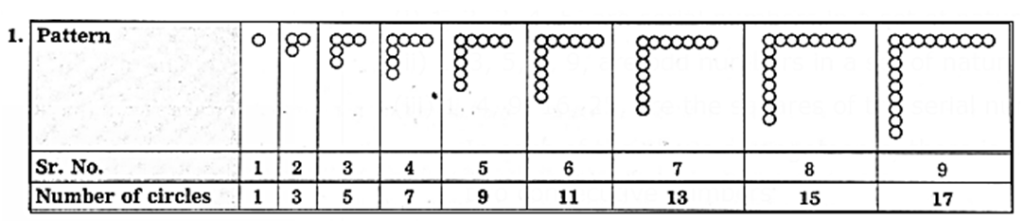
• The formula for the this pattern : 2n — 1, where n = 1, 2, 3,
• g. 5^th term = 2(5) — 1 = 9

• The formula for the this pattern : 3n + 2, where n = 1, 2, 3
• g. 4^th term = 3(4)+2= 14

Terms in a sequence :

• In a sequence, ordered terms are represented as t₁, t₂, t₃, . . . . .t_n . . .
• If the sequence is infinite, for every positive integer n, there is a term t_n.

Activity I : Some sequences are given below. Show the positions of the terms by t₁, t₂, t₃, . . . .

(1) 9, 15, 21, 27, . . .      Here t₁= 9, t₂= 15, t₃= 21, . . .

(2) 7, 7, 7, 7, . . .            Here t₁= 7, t₂= 7, t₃= 7, . . .

(3) —2, —6, —10, —14, . . .   Here t₁= —2, t₂= —6, t₃= —10, . . .

The relation in sequences : Examples :

(1) 1, 4, 7, 10, 13,  ….

(2) 6, 12, 18, 24,  …..

(3) 3, 3, 3, 3, …..

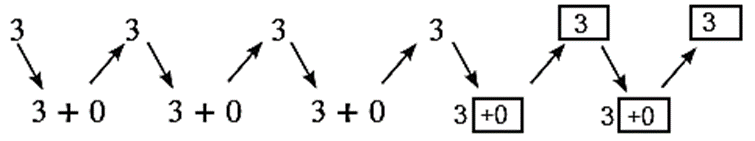
(4) 4, 16, 64, ……

(5) —1, —1.5, —2, —2.5, …….

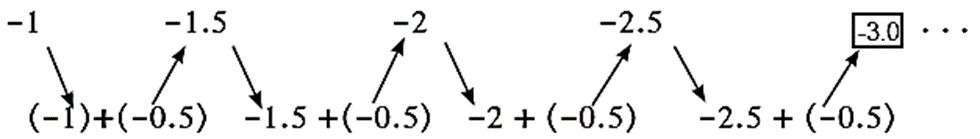
(6) 1³, 2³, 3³, 4³ ……

• In the sequences (1), (2), (3), (5), We get the next term by adding a fixed number to the previous term. This type of sequence is called Arithmetic progression.
• The sequence (4) is not an arithmetic progression. Here, we get the next term by multiplying a fixed number to the previous term. This type of sequence is called Geometric progression.
• The sequence (6) is neither an A.P. nor a G.P.

Arithmetic Progression :

Some sequences are given below. For every sequence write the next three terms.

(1) 100, 70, 40, 10, . . .

Ans :

(2) —7, —4, —1, 2, . . .

Ans :

(3) 4, 4, 4, . . .

Ans :

• In each sequence above, every term is obtained by adding a particular number to the previous term. The difference between two consecutive terms is constant.
• The difference in ex. (i) is negative, in ex. (ii) it is positive and in ex. (iii) it is zero. If the difference between two consecutive terms is constant, then it is called the common difference and is generally denoted by letter ‘d’.

Remember : (1) In a sequence if difference (tn +1— tn) is constant then the sequence is called an arithmetic progression. (2) In an A.P. the difference between two consecutive terms is constant and is denoted by d. (3) Difference d can be positive, negative or zero. (4) In an A.P. if the first term is a, and common difference is d then the terms in the sequence are a, (a + d), (a + 2d), . . . Example of Infinite A.P. : 3, 6, 9, 12, 15, …. This is an infinite A.P. of the natural numbers divisible by 3

nth term of an A. P. :

Formula for the nth term :

Generally in the A.P. t₁, t₂, t₃, . . . If first term is a and common difference is d,

t₁= a

t₂= t₁+ d = a + d = a + (2 — 1) d

t₃= t₂+ d = a + d + d = a + 2d = a + (3 — 1)d

t₄= t₃+ d = a + 2d + d = a + 3d = a +(4 — 1)d

We get the formula t_n= a +(n — 1) d.

 

Q. Find the 100th term of the A.P. 5, 8, 11, 14, . . . also check whether 61 is in this A.P.

Q. Kabir’s mother keeps a record of his height on each birthday. When he was one year old, his height was 70 cm, at 2 years he was 80 cm tall and 3 years he was 90 cm tall. His aunt Meera was studying in the 10th class. She said, ‘‘it seems like Kabir’s height grows in Arithmetic Progression’’. Assuming this, she calculated how tall Kabir will be at the age of 15 years when he is in the 10th ! She was shocked to find it. You too assume that Kabir grows in A.P. and find out his height at the age of 15 years.

Sum of first n terms of an A. P. :

Derivation of the formula :

Consider an A.P. : a, a+d, a +2d,… , [a+(n— 1)d], Where a is the first term and d is the common difference.

The sum of the first n terms of an A.P. is

S_n = a + [a+d] +...+ [a+(n—2)d] + [a + (n — 1)d]  …..(1)

Reversing the terms and rewriting the expression, we get,

S_n = [a+(n—1)d] + [a+(n—2)d] +... + [a +d] + a    ….(2)

Adding equations (1) and (2),

2S_n = [2a+(n—1)d] + [2a+ (n — 1) d] +…..  + [2a + (n — 1)d] ...(n times)

∴ 2S_n = n [2a + (n — 1) d]

∴ S_n  = \(\frac{n}{2}\)[2a + (n — 1) d]

The sum of the first n terms of an A.P. whose first term is a and the common difference d is

S_n  = \(\frac{n}{2}\)[2a + (n — 1) d]

A1so, S_n  = \(\frac{n}{2}\)[a + a + (n — 1) d]

∴ S_n  = \(\frac{n}{2}\)[t₁ + t_n]       …[t₁ = a and t_n = a + (n — 1)d]

If we take t_n as the last term l, then

S_n  = \(\frac{n}{2}\)[ a + l ]

 

Q. Derive the formula for the nth term of the sequence of odd natural numbers and even natural numbers.

Q. Find the sum of the first n (i) natural numbers (ii) odd natural numbers and (iii) even natural numbers.

Q. Find the sum of all odd numbers from 1 to 150

Application of A.P. :

We solve many word problems that arise in daily life using the theory and equations of an A.P.

Examples :

Q. A mixer manufacturing company manufactured 600 mixers in 3rd year and in 7th year they manufactured 700 mixers. If every year there is same growth in the production of mixers then find (i) Production in the first year (ii) Production in 10th year (iii) Total production in first seven years.