Nuclear Chemistry and Radioactivity
Maharashtra State Board-Class-11-Science-Chemistry-Chapter -13
Solutions
Question 1. Choose correct option.
(A) Identify nuclear fusion reaction
(a) \(_1^1\)H + \(_1^1\)H → \(_1^2\)H + \(_1^0\)e
(b) \(_1^2\)H + \(_1^1\)H → \(_2^3\)He
(c) \(_1^3\)H + \(_1^1\)H → \(_1^3\)H + \(_1^1\)p
(b) \(_1^2\)H + \(_1^1\)H → \(_2^3\)He
(B) The missing particle from the nuclear reaction is Al + He → ? + n
(a) \(_{15}^{30}\)P
(b) \(_{16}^{32}\)S
(c) \(_{10}^{14}\)Ne
(d) 14Si
(a) \(_{15}^{30}\)P
(C) \(_{60}^{27}\)CO decays with half−life of 5.27 years to produce \(_{60}^{28}\)Ni . What is the decay constant for such radioactive disintegration ?
(a) 0.132 y−1
(b) 0.138
(c) 29.6 y
(d) 13.8 %
(a) 0.132 y−1
(D) The radioactive isotope used in the treatment of Leukemia is
(a) 60Co
(b) 226Ra
(c) 32P
(d) 226I
(c) 32P
(E) The process by which nuclei having low masses are united to form nuclei with large masses is
(a) chemical reaction
(b) nuclear fission
(c) nuclear fusion
(d) chain reaction
(c) nuclear fusion
Question 2. Explain
(A) On the basis of even−odd of protons and neutrons, what type of nuclides are most stable ?
- Nuclides with even protons and even neutrons are most stable, as they form proton−proton and neutron−neutron pairs, ensuring the stability of the nucleus.
- There is one−third number of stable nuclides with either Z or N odd compared to both are even. But these nuclides are less stable compared to even number of protons and neutrons.
- There are only four stable nuclides with odd Z and odd N. Generally they are unstable due to the presence of two unpaired nucleous and about 2% of the earth's crust consists of such nuclides.
(B) Explain in brief, nuclear fission.
Nuclear fission :
- This involves the splitting of a heavy nucleus of an atom into two nearly equal fragments along with the release of large amount of energy.
- Consider the nuclear fission of 235U isotope by neutron.
\(_{92}^{232}\)U + \(_1^0\)n → \(_{56}^{142}\)Ba + 36Kr + 3 \(_1^0\)n + energy
- Each fission may lead to different products. The mass of fission products is less than the mass of parent nucleus and energy equivalent to loss in mass or mass defect is emitted in the reaction.
- The reaction indicates that fission of one 235U nucleus emits 3 neutrons which further bring about the fission of three 235U nuclei and this process continues resulting a chain reaction releasing a large amount of energy in a short time.
- Fission of 235U takes place by 400 ways yielding 800 fission products many of which are radioactive producing new elements on disintegration.
- The energy released per fission is about 200 MeV. This self sustained chain reaction is highly explosive.
- This energy may be utilised for destructive purposes, defence purpose as well as for peaceful purposes (nuclear reactor−power plant), etc.
(C) The nuclides with odd number of both protons and neutrons are the least stable. Why ?
The nuclides with odd number of both protons and neutrons are least stable due to absence of a partner nucleon for pairing with one odd nucleon. The presence of unpaired nucleons imparts instability to the nuclides.
For example, \(_{93}^{237}\)Np, \(_{97}^{247}\)Bk.
(D) Referring the stability belt of stable nuclides, which nuclides are −β and +β emitters ? Why ?
- Beta decay occurs when an unstable nucleus emits a beta particle and energy. A beta particle is either an electron or a positron. An electron is a negatively charged particle, and a positron is a positively charged electron (or anti−electron).
- When the beta particle is an electron, the decay is called beta−minus (ß−) decay. In beta−minus decay, a neutron breaks down to a proton and an electron, and the electron is emitted from the nucleus.
- When the beta particle is a positron, the decay is called beta−plus (ß+) decay. In beta−plus decay, a proton breaks down to a neutron and a positron, and the positron is emitted from the nucleus.
- Thus, beta−minus decay occurs when a nucleus has too many neutrons relative to protons (i.e., N/Z >1) and beta−plus decay occurs when a nucleus has too few neutrons relative to protons (i.e., N/Z <1).
- The nuclides having N/Z > 1, have a tendency to lose ß− ( e) reducing the ratio N/Z and attaining stability.
\(_{Z}^{A}\)X → \(_{Z+1}^{A}\)Y + \(_{-1}^{0}\)e (ß−).
- The nuclides having N/Z < 1 have a tendency to lose β+ e or position to attain stability).
\(_{Z}^{A}\)X → \(_{Z-1}^{A}\)Y + \(_{+1}^{0}\)e (ß+).
(E) Explain with an example each nuclear transmutation and artificial radioactivity. What is the difference between them ?
- Nuclear transmutation is transformation of a stable nucleus into another stable or unstable nucleus.
(_{7}^{14}\)N + (_{2}^{4}\)He → (_{8}^{17}\)O + (_{1}^{1}\)H
- Artificial radioactivity is nuclear transmutation in which a stable nucleus is converted into radioactive nucleus by high velocity projectiles.
(_{5}^{10}\)B + (_{2}^{4}\)He → (_{7}^{13}\)N + (_{0}^{1}\)n
Stable + Projectile → Radioactive
- Thus, the new isotope formed in artificial radioactivity is unstable and radioactive whereas in nuclear transmutation the new isotope formed is stable.
(F) What is binding energy per nucleon ? Explain with the help of diagram how binding energy per nucleon affects nuclear stability ?
The energy released equivalent to the mass lost (defect) during the formation of an atom (or nuclide) is called nuclear binding energy.
Binding energy per nucleon = \(\bar{B}\) = \(\frac{Δm×931.4}{A}\)
The nuclear stability can be explained by plotting binding energy per nucleon as a function of mass number A of various nuclides. The parabolic curve obtained is called binding energy curve.
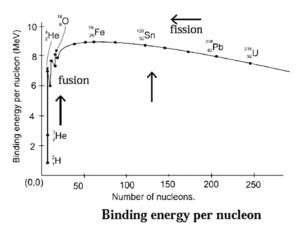
Inferences from binding energy curve :
- Light nuclides (A < 30) : For light nuclides, the peaks in curve with A values in multiples of 4 are very stable. They are \(_{2}^{4}\)He, \(_{6}^{12}\)C, \(_{8}^{16}\)O
- Medium mass nuclides : (30 < A < 90) : In these nuclides, the binding energy per nucleon, \(\bar{B}\) increases from 8 MeV for A = 6 to 8.3 MeV for A having values 28 to 32 and further remains nearly constant 8.5 MeV. The nuclides falling on the maximum are most stable. 56Fe having \(\bar{B}\) values 8.79 MeV is extremely stable.
- Heavy nuclides (A > 90) : For heavy nuclides the \(\bar{B}\) values decrease from 8.79 to 7.7 MeV. 209Bi is the most stable nuclide. Beyond this all nuclides are unstable and radioactive.
(G) Explain with example α−decay.
Alpha decay :
- The emission of α −particle from the radioactive nuclei is called α −decay.
- α −particle has +2 unit charge and 4 u mass.
- Hence on−particle is identified with helium nucleus and designated with
- On emission of α −particle, the parent element loses 2 protons and 2 neutrons, thus losing 4 u mass.
- The daughter element thus formed has mass 4 units less and charge or atomic number less by 2 units than its parent element.
\(_{Z}^{A}\)X → \(_{Z-2}^{A-4}\)Y + \(_{2}^{4}\)He
Parent → Daughter + α-particle
\(_{88}^{226}\)Ra → \(_{88}^{226}\)Rn + \(_{2}^{4}\)He
Parent → Daughter + α-particle
- The daughter element formed occupies two places (groups) to the left of the parent element in the periodic table.
(H) Energy produced in nuclear fusion is much larger than that produced in nuclear fission. Why is it difficult to use fusion to produce energy ?
Nuclear fusion offers greater energy than nuclear fission but requires extremely high temperatures, surpassing 108K which is achieved by nuclear fission. Hence, nuclear fusion cannot be used to produce energy.
(I) How does N/Z ratio affect the nuclear stability ? Explain with a suitable diagram.
The nuclear stability can be explained with the help of neutrons to proton (N/Z) ratio.
- When for stable nuclides the number of neutrons (N) is plotted as a function of number of protons (Z), a curve is obtained. This curved belt is called nuclear stability zone.

- The nuclides which exist outside the stability zone are unstable and radioactive.
- A straight line below the belt has equal number of neutrons and protons or the slope N/Z =1.
- Nuclides lighter than \(_{20}^{40}\)Ca are stable and have N = Z.
- For stable nuclides heavier than calcium, the ratio N/Z is greater than one.
- In heavier nuclides with the increasing number of protons there arises large coulombic repulsion among them. With increased number of neutrons the protons in the nuclei get separated decreasing the repulsion and increasing stability. Therefore, heavier nuclides require more number of neutrons than protons to attain a stability.
(J) You are given a very old sample of wood. How will you determine its age ?
The age of the wood sample can be determined by radiocarbon dating as 14C becomes a part of a plant due to the photosynthesis reaction (i.e., absorption of [14CO2 + 12CO2].
The activity (N) of a given wood sample and that of a fresh sample of the live plant (No) is measured, where, No denotes the activity of the given sample at the time of death.
The age of the given wood sample, can be determined by applying following Formulae:
t = \(\frac{2.303}{λ}\)log10\(\frac{N_0}{N}\)
where λ = \(\frac{0.693}{5730y}\) = 1.21 × 10−4 y−1
Question 3. Answer the following question
(A) Give example of mirror nuclei.
\(_{6}^{13}\)C and \(_{7}^{13}\)N are mirror nuclei in which the number of protons and neutrons differ by 1.
(B) Balance the nuclear reaction: \(_{54}^{118}\)Xe → ? + \(_{54}^{118}\)I
\(_{54}^{118}\)Xe → γ + \(_{54}^{118}\)I
(C) Name the most stable nuclide known. Write two factors responsible for its stability.
The most stable nuclide known is \(_{26}^{56}\)Fe.
- It has two magic numbers namely 26 protons and 56 − 26 = 30 neutrons.
- They have even Z and N. This gives extra stability to the nuclide.
(D) Write relation between decay constant of a radioelement and its half life.
The relation between decay constant (λ) and half life (t1/2) of a radioelement is,
t1/2 = \(\frac{0.693}{λ}\)
(E) What is the difference between an α−particle and helium atom ?
- The helium atom is composed of 2 protons and 2 neutrons (or 1 neutron) along with 2 electrons in the outer shell.
- On the other hand, α−particle constitutes 2 protons and 2 neutrons bound together to form a particle that is similar to helium (except the presence of electrons).
- Helium is one of the inert gas which is stable (duplet complete) whereas α−particle is unstable and highly reactive.
(F) Write one point that differentiates nuclear reactions from chemical reactions.
| Nuclear reactions | Chemical reactions. |
| Elements or isotopes of one element are converted into another element in a nuclear reaction. | Rearrangement of atoms by breaking and forming of chemical bonds. |
| Isotopes of an element behave differently. | Different isotopes of an element have same behaviour. |
| In addition to electrons, protons, neutrons, other elementary particles may be involved. | Only outer shell electrons take part in the chemical reaction. |
| The nuclear reaction is accompanied by a large amount of energy change. e.g. The nuclear transformation of 1 g of Uranium − 235 release 8.2 x 107 kJ | The chemical reaction is accompanied by relatively small amounts of energy.
e.g. chemical combustion of 1.0 g methane releases only 56 kJ energy. |
| The rates of reaction are influenced by temperature, pressure, concentration, and catalyst. | The rate of nuclear reactions is unaffected by temperature, pressure, and catalyst. |
(G) Write pairs of isotones and one pair of mirror nuclei from the following :
\(_{5}^{10}\)B, \(_{6}^{12}\)C, \(_{13}^{27}\)Al, \(_{6}^{11}\)C, \(_{14}^{28}\)S:
Pairs of Isotones :
(i) \(_{5}^{10}\)B, and \(_{6}^{11}\)C, (ii) \(_{13}^{27}\)Al, and \(_{14}^{28}\)S
Mirror nuclei: Since there are no isobars the given set of nuclides does not contain a pair of mirror nuclei.
(H) Derive the relationship between half life and decay constant of a radioelement.
The decay constant A of a radioelement is represented as,
λ = \(\frac{2.303}{t}\)log10\(\frac{N_0}{N}\)
where No is initial number of radioactive atoms at t − 0 and N is after time t.
∴ t = \(\frac{2.303}{λ}\)log10\(\frac{N_0}{N}\)
At half life period, t = t1/2 the number of atoms becomes N = N0/2
∴ t1/2 = \(\frac{2.303}{λ}\)log10\(\frac{N_0}{N_0/2}\)
= \(\frac{2.303}{λ}\)log10 2
= \(\frac{2.303×0.3010}{λ}\)
= \(\frac{0.693}{λ}\)
(I) Represent graphically log10 (activity/dps) versus t/s. What is its slope ?
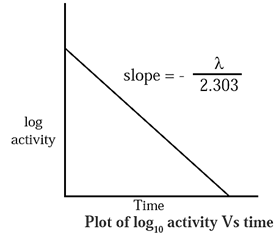
If a is activity of a radioelement then,
log10 a = \(-\frac{λt}{2.303}\) + log10 a0
where a0 is initial activity.
When log10 a is plotted versus t a straight line with negative slope is obtained,
∴ slope = \(-\frac{λt}{2.303}\)
(J) Write two units of radioactivity. How are they interrelated ?
Units of radioactivity : Rate of radioactive decay is expressed in dps.
(i) The unit for the radioactivity is curie (Ci).
1 Ci = 3.7 x 1010 dps (disintegrations per second)
(ii) Another unit of radioactivity is Becquerel (Bq)
1 Bq = 1 dps. Thus, 1Ci = 3.7 x 1010 dps = 3.7 x 1010 Bq
(K) Half life of 24Na is 900 minutes. What is its decay constant?
Given : t1/2 = 900 min. λ = ?
λ = \(\frac{0.693}{t_{1/2}}\) = \(\frac{0.693}{900}\) = 7.7 x 10−4 min−1
(L) Decay constant of 197Hg is 0.017 h−1. What is its half life ?
Given : λ = 0.017 h−1, t1/2 = ?
t1/2 = \(\frac{0.693}{λ}\) = \(\frac{0.693}{0.017}\) = 40.76 h
(M) The total binding energy of 58Ni is 508 MeV. What is its binding energy per nucleon ?
Given : Total B.E. = 508 MeV; A = 58, B.E. per nucleon = ?
B.E. per nucleon = \(\frac{\text{Total B.E.}}{\text{Number of nucleons}}\)
= \(\frac{508}{A}\)
= \(\frac{508}{58}\) = 8.759 MeV
Binding energy per nucleon = 8.759 MeV.
(N) Atomic mass of \(_{16}^{32}\)S is 31.97 u. If masses of neutron and H atom are 1.0087 u and 1.0078 u respectively. What is the mass defect ?
Given : Z = 16, A = 32; m = 31.97 u; mH = 1.0078 u; mn = 1.0087 u
Mass defect = Δm
= Z × mH + (A − Z)mn − m
= 16 × 1.0078 + (32 − 16)×1.0087 − 31.97
=16.1248 + 16.1392 − 31.97
= 0.294 u
Mass defect = Δm =0.294 u.
(O) Write the fusion reactions occurring in the Sun and stars.
\(_{1}^{1}\)H + \(_{1}^{1}\)H → \(_{1}^{2}\)H + \(_{+1}^{0}\)e
\(_{1}^{1}\)H + \(_{1}^{2}\)H → \(_{2}^{3}\)He
\(_{2}^{3}\)He + \(_{2}^{3}\)He → \(_{2}^{4}\)He + 2\(_{1}^{1}\)H
\(_{2}^{3}\)He + \(_{1}^{1}\)H → \(_{2}^{4}\)He + \(_{+1}^{0}\)e
- During nuclear fusion enormous energy is released. High temperature is required for nuclear fusion reaction which is attained by carrying out nuclear reaction prior to it. These reactions occur in the Sun and stars continuously.
(P) How many α and β − particles are emitted in the transmutation \(_{90}^{232}\)Th → \(_{92}^{208}\)Pb ?
Decrease in mass number = 232 − 208 = 24.
Since a emission decreases mass number by 4, there must be emission of 6 α particles.
Since each α particle emission decreases atomic number by 2,
final atomic number should be 90 − 12 = 78.
But since each β particle emission increases atomic number by 1, there must be emission of 4 β particles.
∴ 6 α and 4 β particles are emitted.
(Q) A produces B by ∝− emission. If B is in the group 16 of periodic table, what is the group of A ?
A → B + \(_{2}^{4}\)He (∝)
Group 18 Group 16
A is in group 18 of periodic table.
(R) Find the number of α and β− particles emitted in the process \(_{86}^{222}\)Rn → \(_{84}^{214}\)Po.
- The emission of one α−particle decreases the mass number by 4 whereas the emission of ß−particles has no effect on the mass number.
- Net decrease in mass number = 222 − 214 = 8. This decrease is only due to α−particle. Hence, number of α −particle emitted = 8/4 = 2
- Now, the emission of one α −particle decreases the atomic number by 2 and one ß−particle emission increases it by 1.
- The net decrease in atomic number = 86 − 84 = 2
- The emission of 2 α−particles causes a decrease in the atomic number by 4. However, the actual decrease is only 2. It means atomic number increases by 2. This increase is due to the emission of 2 ß−particles.
Thus, 2 α and 2 B−particles are emitted.
Question 4. Solve the problems
(A) Half life of 18F is 110 minutes. What fraction of 18F sample decays in 20 minutes ?
Given : t1/2 = 110 min; t = 20 min. Fraction of 19F sample decays = ?
λ = \(\frac{0.693}{t_{1/2}}\) = \(\frac{0.693}{110}\) = 6.3 x 10−3 min−1
λ = \(\frac{2.303}{t}\)log10\(\frac{N_0}{N}\)
∴ log10\(\frac{N_0}{N}\) = \(\frac{λt}{2.303}\) = \(\frac{6.3×10^{-3}×20}{2.303}\) = 0.05471
∴ \(\frac{N_0}{N}\) = Antilog 0.05471 = 1.134
∴ Fraction of sample left = \(\frac{N_t}{N_0}\) = \(\frac{1}{1.134}\) = 0.8818
∴ Fraction of sample decayed = 1 − 0.8818 = 0.1182
(B) Half life of 35S is 87.8 d. What percentage of 35S sample remains after 180 d ?
Given : t1/2 = 87.8 d; t = 180 d; Percentage of sample left = ?
λ = \(\frac{0.693}{t_{1/2}}\) = \(\frac{0.693}{87.8}\) = 7.893 x 10−3 d−1
λ = \(\frac{2.303}{t}\)log10\(\frac{N_0}{N}\)
∴ log10\(\frac{N_0}{N}\) = \(\frac{λt}{2.303}\) = \(\frac{7.893×10^{-3}×180}{2.303}\) = 0.6169
∴ \(\frac{N_0}{N}\) = Antilog 0.6169 = 4.139
∴ Fraction left = \(\frac{N_t}{N_0}\) = \(\frac{1}{4.139}\) = 0.2416
∴ Percentage of sample remained = 0.2416 × 100 = 24.16%
Percentage of sample 35S left = 24.16.
(C) Half life 67Ga is 78 h. How long will it take to decay 12% of sample of Ga ?
Given : t1/2 = 78 h; t = ? for decay of 12% of sample of Ga
λ = \(\frac{0.693}{t_{1/2}}\) = \(\frac{0.693}{78}\) = 8.885 x 10−3 h−1
λ = \(\frac{2.303}{t}\)log10\(\frac{N_0}{N}\)
∴ t = \(\frac{2.303}{λ}\)log10\(\frac{N_0}{N}\)
= \(\frac{2.303}{8.885×10^{-3}}\)log10\(\frac{100}{(100-12)}\)
= \(\frac{2.303}{8.885×10^{-3}}\)log10 1.136
= \(\frac{2.303×0.05538}{8.885×10^{-3}}\) = 14.35 h
Time to decay of 12% of sample of Ga = 14.35 h
(D) 0.5 g Sample of 201Tl decays to 0.0788 g in 8 days. What is its half life ?
Given : m0 = 0.5 g; m = 0.0788 J; t = 8 days; t1/2 = ?
λ = \(\frac{2.303}{t}\)log10\(\frac{m_0}{m}\)
= \(\frac{2.303}{8}\)log10\(\frac{0.5}{0.0788}\)
= \(\frac{2.303}{8}\)log10 6.345
= \(\frac{2.303×0.8024}{8}\) = 0.231 d−1
t1/2 = \(\frac{0.693}{λ}\) = \(\frac{0.693}{0.231}\) = 3.0 d
Half life, t1/2 = 3.0 d.
(E) 65% of 111In sample decays in 4.2 d. What is its half life ?
Given : Percentage decay = 65%; t = 4.2 d; t1/2 = ?
Percentage of element left = 100 − 65 = 35%
λ = \(\frac{2.303}{t}\)log10\(\frac{N_0}{N}\)
= \(\frac{2.303}{4.2}\)log10\(\frac{100}{35}\)
= \(\frac{2.303}{4.2}\)log10 2.857
= \(\frac{2.303×0.4559}{4.2}\) = 0.25 d−1
t1/2 = \(\frac{0.693}{λ}\) = \(\frac{0.693}{0.25}\) = 2.772 d
Half life, t1/2 = 2.772 d.
(F) Calculate the binding energy per nucleon of \(_{36}^{84}\)Kr whose atomic mass is 83.913 u. (Mass of neutron is 1.0087 u and that of H atom is 1.0078 u).
Given : For \(_{36}^{84}\)Kr, Z = 36, A = 84, mH = 1.0078 u, mn = 1.0087 u, m = 83.913 u
B.E. per nucleon = ?
Δm = Z x mH + (A − Z) x mn − m
= 36 × 1.0078 + (84 − 36) × 1.0087 − 83.913
= 36.2808 + 48 × 1.0086 − 83.913
= 36.2808 + 48.4176 − 83.913
= 0.7854 u
B.E. per nucleon = \(\frac{Δm×931.4}{A}\) = \(\frac{0.7854×931.4}{84}\) = 8.708 MeV
B.E. per nucleon = 8.708 MeV.
(G) Calculate the energy in Mev released in the nuclear reaction \(_{77}^{174}\)Ir → \(_{75}^{170}\)Re + \(_{2}^{4}\)He Atomic masses : Ir = 173.97 u, Re = 169.96 u and He = 4.0026 u
Given : Atomic masses :
mIr =173.97 u; mRe = 169.96 u; mHe = 4.0026 u
\(_{77}^{174}\)Ir → \(_{75}^{170}\)Re + \(_{2}^{4}\)He
Δm = (Total mass of reactants) – (Total mass of products)
= mIr− (mRe + mHe)
= 173.97 − (169.96 + 4.0026)
= 173.97 − 173.9626
= 7.4 × 10−3 u
Energy released, E = Δm x 931.4 = 7.4 × 10−3 × 931.4 = 6.892 MeV
Energy released = 6.892 MeV.
(H) A 3/4 of the original amount of radioisotope decays in 60 minutes. What is its half life ?
If N0 = 1 then N = 1 − 3/4 = 1/4 ; t = 60 min. t1/2 = ?
λ = \(\frac{2.303}{t}\)log10\(\frac{N_0}{N}\)
= \(\frac{2.303}{60}\)log10\(\frac{1}{1/4}\)
= \(\frac{2.303}{60}\)log10 4
= \(\frac{2.303×0.6021}{60}\) = 0.02311 min−1
t1/2 = \(\frac{0.693}{λ}\) = \(\frac{0.693}{0.02311}\) = 30 min
Half life, t1/2 = 30 min.
(I) How many ∝−particles are emitted by 0.1 g of 226Ra in one year?
Given : Mass of Radium = 0.1 g, t = 1 ∴ y = 1 x 365 x 24 x 60 x 60 s; Number of particles emitted = ?
Disintegrations per year = 0.1 x 3.7 × 1010 × 1 x 365 × 24 × 60 × 60 = 1.167 × 1017
Number of ∝−particles emitted = 1.167 x 1017.
(J) A sample of 32P initially shows activity of one Curie. After 303 days the activity falls to 1.5 × 104 dps. What is the half life of 32P ?
Given : No = 1Ci = 3.7 x 1010 dps; Nt = 1.5 ×104 dps; t = 303 d; t1/2 =?
λ = \(\frac{2.303}{t}\)log10\(\frac{N_0}{N}\)
= \(\frac{2.303}{3.3}\)log10\(\frac{3.7×10^{10}}{1.5×10^4}\)
= \(\frac{2.303}{3.3}\)log10 2.467 × 106
= \(\frac{2.303×6.3992}{3.3}\) = 0.04858
t1/2 = \(\frac{0.693}{λ}\) = \(\frac{0.693}{0.04858}\) = 14.27 d
Half life, t1/2 = 14.27 d.
(K) Half life of radon is 3.82 d. By what time would 99.9 % of radon will be decayed.
Given : t1/2 = 3.82 d; Decay = 99.9% ∴ N = 100 − 99.9 = 0.1; t =?
λ = \(\frac{0.693}{t_{1/2}}\) = \(\frac{0.693}{3.82}\) = 0.1814 d−1
λ = \(\frac{2.303}{t}\)log10\(\frac{N_0}{N}\)
∴ t = \(\frac{2.303}{λ}\)log10\(\frac{N_0}{N}\)
= \(\frac{2.303}{0.1814}\)log10\(\frac{100}{0.1}\)
= \(\frac{2.303×3}{0.1814}\) = 38.08 d
Time required = 38.08 d
(L) It has been found that the Sun’s mass loss is 4.34 × 109 kg per second. How much energy per second would be radiated into space by the Sun ?
Given :
Loss in mass Δm = 4.34 x 109 kg s−1 = 4.34 × 1012 g s−1 = \(\frac{4.34×10^{12}}{1.66×10^{-24}}\) u s−1
Energy radiated = Δm x 931.4
= \(\frac{4.34×10^{12}}{1.66×10^{-24}}\) x 931.4 MeV s−1
= \(\frac{4.34×10^{12}}{1.66×10^{-24}}\) x 931.4 x 106 eV s−1
= \(\frac{4.34×10^{12}}{1.66×10^{-24}}\) x 931.4 x 106 × 1.6 × 10−19 J s−1
= \(\frac{4.34×10^{12}}{1.66×10^{-24}}\) x 931.4 x 106 × 1.6 × 10−22 kJ s−1
= 3.896 x 1023 kJ s−1
Energy released = 3.896 x 1023 kJ s−1
(M) A sample of old wood shows 7.0 dps/g. If the fresh sample of tree shows 16.0 dps/g, How old is the given sample of wood ? Half life of 14C 5730 y.
Given : Initial rate of disintegration = R0 = 16.0 dps g−1 , Final rate of disintegration = R = 7.0 dps g−1 , t1/2 = 5730 y; t = ?
λ = \(\frac{0.693}{t_{1/2}}\) = \(\frac{0.693}{5730}\) = 1.209 x 10−4 y−1
λ = \(\frac{2.303}{t}\)log10\(\frac{R_0}{R}\)
∴ t = \(\frac{2.303}{λ}\)log10\(\frac{R_0}{R}\)
= \(\frac{2.303}{1.209×10^{-4}}\)log10\(\frac{16}{7}\)
= \(\frac{2.303}{1.209×10^{-4}}\)log10 2.286
= \(\frac{2.303×0.3591}{1.209×10^{-4}}\) = 6840 y
Age of wood sample = 6840 y.
PDF : Class-11-Chemistry-Chapter-13-Nuclear Chemistry and Radioactivity- Notes
PDF : Class-11-Chemistry-Chapter-13-Nuclear Chemistry and Radioactivity-Solution
All 16 Chapters Notes -11-Chemistry-(16 PDF) Rs.132
All 16 Chapters-Solutions-11-Chemistry- (16 PDF) Rs.128
All 16 Chapters-Notes+Solutions-11-Chemistry- (32 PDF) Rs.228
Main Page : – Maharashtra Board Class 11th-Chemistry – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter-12-Chemical Equilibrium – Online Solutions
Next Chapter : Chapter-14-Basic Principles of Organic Chemistry – Online Solutions