Solutions
Practice Set 5.1
Question 1.1.
How many possibilities are there in each of the following?
(1) Vanita knows the following sites in Maharashtra. She is planning to visit one of them in her summer vacation.
Ajintha, Mahabaleshwar, Lonar Sarovar, Tadoba wild life sanctuary, Amboli, Raigad, Matheran, Anandavan.
There are 8 places in list for planning to visit.
Therefore, Vanita has 8 possibilities of selecting any one of them.
(2) Any day of a week is to be selected randomly.
There are 7 days in a week.
Therefore, there are 7 possbilities of selecting any one day randomly.
(3) Select one card from the pack of 52 cards.
There are 52 cards.
Therefore, there are 52 possibilities of selecting one card.
(4) One number from 10 to 20 is written on each card. Select one card randomly.
There are 11 numbers from 10 to 20 written on the cards.
Therefore, there are 11 possibilities of selecting one card randomly.
Practice Set 5.2
Question 2.1
For each of the following experiments write sample space ‘S’ and number of sample points n(S).
(1) One coin and one die are thrown simultaneously.
(2) Two digit numbers are formed using digits 2, 3 and 5 without repeating a digits.
(1) The sample space for a coin
S = {H,T}, ∴ n(S)=2
The sample space for a die
S = (1, 2, 3, 4, 5, 6) ∴ n(S) = 6
∴ if a coin is tossed and a die is thrown simultaneously, the sample space
S = {H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6} ∴ n(S) = 12
(2) The two-digit numbers formed using digits 2,3,5
S = {23, 25, 32, 35, 52, 53}, ∴ n(S) = 6.
Question 2.2.
The arrow is rotated and it stops randomly on the disc. Find out on which colour it may stop.
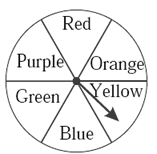
There are six colours on the disc. The arrow can stop on any of the colours.
∴ S = {Red, Orange, Yellow, Blue, Green, Purple }
∴ n(S)= 6.
Question 2.3.
In the month of March 2019, find the days on which the date is a multiple of 5. (see the given page of the calendar)
The dates multiples of 5 are 5, 10, 15, 20, 25, 30.
S={Tuesday, Sunday, Friday, Wednesday, Monday, Saturday }
∴ n(S) = 6.
Question 2.4.
Form a ‘Road safety commitee’ of two, from 2 boys (B1, B2) and 2 girls(G1, G2).
Complete the following activity to write the sample space.
(a) Committee of 2 boys = […..]
(b) Committee of 2 girls = [….]
(c) Committee of one boy and one girl = [B1G1] [….] […..] [……]
∴ Sample space = {..., ..., ..., ..., ..., ...}
(a) Committee of 2 boys = [B1 B2]
(b) Committee of 2 girls = [G1 G2]
(c) Committee of one boy and one girl = [B1 G1] [B1 G2] [B2 G1] [B2 G2]
∴ Sample space = { B1 B2, G1 G2, B1 G1, B1 G2, B2 G1, B2 G2}
Practice Set 5.3
Question 3.1.
Write sample space ‘S’ and number of sample point n(S) for each of the following experiments. Also write events A, B, C in the set form and write n(A), n(B), n(C).
(1) One die is rolled,
Event A : Even number on the upper face.
Event B : Odd number on the upper face.
Event C : Prime number on the upper face.
One die is rolled.
∴ the sample space S = {1, 2, 3, 4, 5, 6}. ∴ n(S) = 6.
Event A : Even number on the upper face.
∴ A = {2, 4, 6} ∴ n(A) = 3.
Event B : Odd number on the upper face.
∴ B = {1, 3, 5}. ∴ n(B) = 3
Event C : Prime number on the upper face.
∴ C = {2, 3, 5}, ∴ n(C) = 3.
(2) Two dice are rolled simultaneously,
Event A : The sum of the digits on upper faces is a multiple of 6.
Event B : The sum of the digits on the upper faces is minimum 10.
Event C : The same digit on both the upper faces.
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
∴ n(S) = 36.
Event A : The sum of the digits on upper faces is a multiple of 6.
∴ A = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1), (6, 6) }. ∴ n(A) =6.
Event B : The sum of the digits on upper faces is minimum 10.
∴ B = {(4, 6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6) }. ∴ n(B) = 6.
Event C : The same digit on both the upper faces.
∴ C= {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6) }. ∴ n(C) = 6.
(3) Three coins are tossed simultaneously.
Condition for event A : To get at least two heads.
Condition for event B : To get no head.
Condition for event C : To get head on the second coin.
Three coins are tossed simultaneously.
∴ the sample space,
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}. ∴ n(S) = 8.
Condition for event A : To get at least two heads.
∴ A = {HHH, HHT, HTH, THH} ∴ n(A) = 4.
Condition for event B : To get no head.
∴ B = {TTT} ∴ n(B) = 1.
Condition for event C: To get head on the second coin.
∴ C = {HHH, HHT, THH, THT } ∴ n(C) = 4.
(4) Two digit numbers are formed using digits 0, 1, 2, 3, 4, 5 without repetition of the digits.
Condition for event A : The number formed is even
Condition for event B : The number formed is divisible by 3.
Condition for event C : The number formed is greater than 50.
As we have to form two-digit numbers, 0 cannot be at tens place.
The sample space
S = {10, 12, 13, 14, 15, 20, 21, 23, 24, 25, 30, 31, 32, 34, 35, 40, 41, 42, 43, 45, 50, 51, 52, 53, 54}, ∴ n(S) = 25.
(i) Condition for event A : The number formed is even.
∴ A = {10, 12, 14, 20, 24, 30, 32, 34, 40, 42, 50, 52, 54}, ∴ n(A) = 13.
(ii) Condition for event B : The number is divisible by 3.
∴ B = {12, 15, 21, 24, 30, 42, 45, 51, 54}, ∴ n(B) = 9.
(iii) Condition for event C: The number is greater than 50.
∴ C = {51, 52, 53, 54}, ∴ n(C) = 4.
(5) From three men and two women, environment committee of two persons is to be formed.
Condition for event A : There must be at least one woman member.
Condition for event B : One man, one woman committee to be formed.
Condition for event C : There should not be a woman member.
Here, there are 3 men M1, M2, M3 and 2 women W1, W2.
A committee of two is to be formed.
∴ the sample space
S = {M1M2, M1M3, M2M3, M1W1, M1W2, M2W1, M2W2, M3W1, M3W2, W1W2}
∴ n(S) = 10
(i) Condition for event A : There must be at least one woman.
∴ A = {M1W1, M1W2, M2W1, M2W2, M3W1, M3W2, W1W2}, ∴ n(A) = 7.
(ii) Condition for event B : One man, one woman committee to be formed.
∴ B = {M1W1, M1W2, M2W1, M2W2, M3W1, M3W2}, ∴ n(B) = 6.
(iii) Condition for event C: There is no woman in the committee.
∴ C = {M1M2, M1M3, M2M3}, ∴ n(C) = 3.
(6) One coin and one die are thrown simultaneously.
Condition for event A : To get head and an odd number.
Condition for event B : To get a head or tail and an even number.
Condition for event C : Number on the upper face is greater than 7 and tail on the coin.
The sample space for a coin
S = {H, T}, ∴ n(S) = 2.
The sample space for a die
S = (1, 2, 3, 4, 5, 6), ∴ n(S) = 6
∴ if a coin is tossed and a die is thrown simultaneously, the sample space
S = {H1, H2, H3, H4, H5, H6,T1,T2,T3,T4,T5,T6}, ∴ n(S) = 12
(i) Condition for event A : To get a head and an odd number.
∴ A = {H1, H3, H5}, ∴ n(A) = 3.
(ii) Condition for event B : To get a head or tail and an even number.
∴ B = {H2, H4, H6, T2, T4, T6}. ∴ n(B) =6.
(iii) Condition for event C: Number on the upper face is greater than 7 and tail on the coin.
There is no number greater than 6 on a die.
∴ C = Φ, ∴ n(C) = 0.
Practice Set 5.4
Question 4.1.
If two coins are tossed, find the probability of the following events.
(1) Getting at least one head. (2) Getting no head.
Let S be the sample space.
Then S = {HH, HT, TH, TT}. ∴ n(S) = 4.
(1) Let A be the event where at least one head turns up
Then A = {HH, HT, TH}, ∴ n(A) = 3.
P(A) = \(\frac{n(A)}{n(S)}\) , ∴ P(A) = \(\frac{3}{4}\).
(2) Let B be the event where no head turns up.
Then B = {TT} , ∴ n(B) = 1
P(B) = \(\frac{n(B)}{n(S)}\) , ∴ P(B) = \(\frac{1}{4}\).
Answer : (1) \(\frac{3}{4}\) (2) \(\frac{1}{4}\) .
Question 4.2.
If two dice are rolled simultaneously, find the probability of the following events.
(1) The sum of the digits on the upper faces is at least 10.
(2) The sum of the digits on the upper faces is 33.
(3) The digit on the first die is greater than the digit on second die.
Two dice are rolled simultaneously.
∴ the sample space is
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6),
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
∴ n(S) = 36.
(1) Let A be the event that the sum of the digits on the upper faces is at least 10.
Then A = { (4, 6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6) }, ∴ n(A) = 6.
∴ P(A) = \(\frac{n(A)}{n(S)} = \frac{6}{36}\) = \(\frac{1}{6}\).
(2) Let B be the event that the sum of the digits on the upper faces is 33.
The sum of the digits on the upper faces is maximum (6, 6) that is 12.
∴ B = { }. ∴ n(B) = 0
∴ P(B) = \(\frac{n(B)}{n(S)} = \frac{0}{36}\) = 0
(3) Let C be the event that the digit on the first die is greater than the digit on the second die.
Then C = { (2, 1), (3, 1), (3, 2), (4, 1), (4, 2), (4, 3), (5, 1), (5, 2), (5, 3), (5, 4), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5) }, ∴ n(C) = 15.
∴ P(C) = \(\frac{n(C)}{n(S)} = \frac{15}{36}\) = \(\frac{5}{12}\).
Answer : (1) \(\frac{1}{6}\) (2) 0 (3) \(\frac{5}{12}\).
Question 4.3.
There are 15 tickets in a box, each bearing one of the numbers from 1 to 15. One ticket is drawn at random from the box. Find the probability of event that the ticket drawn -
(1) shows an even number. (2) shows a number which is a multiple of 5.
The sample space is
S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}, ∴ n(S) = 15
(1) Let A be the event that the ticket drawn bears an even number.
Then A = {2, 4, 6, 8, 10, 12, 14}, ∴ n(A) = 7
P(A) = \(\frac{n(A)}{n(S)} = \frac{7}{15}\)
(2) Let B be the event that the ticket drawn bears a number which is a multiple of 5.
Then B = {5, 10, 15}, ∴ n(B) = 3
P(B) = \(\frac{n(B)}{n(S)} = \frac{3}{15}\) = \(\frac{1}{5}\).
Answer : (1) \(\frac{7}{15}\) (2) \(\frac{1}{5}\)
Question 4.4.
A two digit number is formed with digits 2, 3, 5, 7, 9 without repetition. What is the probability that the number formed is
(1) an odd number ? (2) a multiple of 5 ?
The sample space is
S= {23, 25, 27, 29, 32, 35, 37, 39, 52, 53, 57, 59, 72, 73, 75, 79, 92, 93, 95, 97}
∴ n(S) = 20
(1) Let A be the event that two-digit odd numbers are formed.
Then A = {23, 25, 27, 29, 35, 37, 39, 53, 57, 59, 73, 75, 79, 93, 95, 97},
∴ n(A) = 16
P(A) = \(\frac{n(A)}{n(S)} = \frac{16}{20}\) = \(\frac{4}{5}\).
(2) Let B be the event that the two-digit number is a multiple of five.
Then B = {25, 35, 75, 95}, ∴ n(B) = 4
P(B) = \(\frac{n(B)}{n(S)} = \frac{4}{20}\) = \(\frac{1}{5}\).
Answer : (1) \(\frac{4}{5}\). (2) \(\frac{1}{5}\).
Question 4.5.
A card is drawn at random from a pack of well shuffled 52 playing cards. Find the probability that the card drawn is -
(1) an ace. (2) a spade.
S is the sample space
∴ n(S) = 52 ….... (There are 52 playing cards)
(1) Let A be the event that the card drawn is an ace.
There are four suits, Spade, Heart, Diamond and Club. Each suit has one ace.
(S) = { A-S, A-H, A-D, A-C}, ∴ n(A) = 4
P(A) = \(\frac{n(A)}{n(S)} = \frac{4}{52}\) = \(\frac{1}{13}\).
(2) Let B be the event that the card drawn is a spade.
There are 13 cards in the suit of spade One spade can be drawn out of 13 spade cards in 13 ways.
∴ n(B) = 13
P(B) = \(\frac{n(B)}{n(S)} = \frac{13}{52}\) = \(\frac{1}{4}\).
Answer : (1) \(\frac{1}{13}\). (2) \(\frac{1}{4}\).
We reply to valid query.