Notes
|
Topics to be learn :
|
Pythagoras theorem : In a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of remaining two sides.
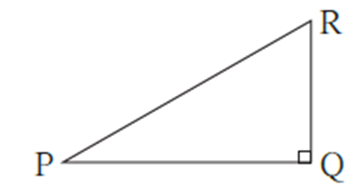
In ΔPQR ∠PQR = 90°
l(PR)2 = l(PQ)2 + l(QR)2
We will write this as, PR2 = PQ2 + QR2
Pythagorean triplet :
In a triplet of positive integers, if the square of the largest number is equal to the sum of the squares of the remaining two numbers, then the group of these three numbers is called a Pythagorean triplet.
e.g. if a, b, c are three positive integers and a is the largest integer and a2 = b2 + c2 then (a, b, c) is a Pythagorean triplet.
Example:
In the triplet ( 11, 60, 61 ) ,
112 = 121, 602 = 3600, 612 = 3721 and 121 + 3600 = 3721
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ 11, 60, 61 is a Pythagorean triplet.
Remember, numbers in Pythagorean triplet can be written in any order.
Formula to find Pythagorean triplet :
If p, q and r are positive integers and p > q then [(p2 + q2), (p2 — q2 ), (2pq)] is a Pythagorean triplet.
(p2 + q2)2 = p4 + 2p2q2 + q4 .......... (I)
(p2 — q2)2 = p4 — 2p2q2 + q4.......... (II)
(2pq)2 = 4p2q2 .......... (III)
∴by (I), (II) and (III) , (p2 + q2)2 = (p2 — q2)2 + (2pq)2
∴ [(p2 + q2), (p2 — q2 ), (2pq)] is Pythagorean Triplet.
This formula can be used to find various Pythagorean triplets by taking different values of p and q.
Example : If a = 5 and b = 3,
a2 + b2 = 34, a2 — b2 = 16 , 2ab = 30.
342 = 1156, 302 = 900, 162 = 256
1156 = 900 + 256
342 = 302 + 162
∴ (34, 16, 30) is a Pythagorean triplet.
Right angled triangle :
A triangle in which one of the angles measure 90° is called a right angled triangle.
In ΔPQR, ∠PQR = 90°.
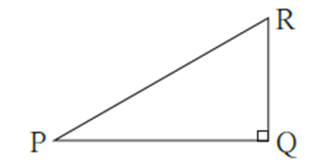
Δ PQR is a right angled triangle. The side opposite to 90° is called the hypotenuse and sides PQ and QR are called perpendicular sides or sides containing the right angle. Hypotenuse is the longest side in the right angled triangle.
Remember, in a right angled triangle, the two angles other than right angle are always acute. In the figure, ∠P and ∠R are acute angles.
Similarity and right angled triangles
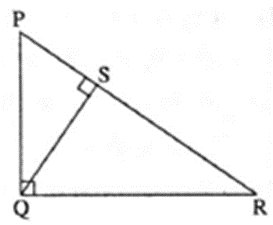
Theorem ; In a right angled triangle, if the altitude is drawn to the hypotenuse, then the two triangles formed are similar to the original triangle and to each other.
Given : In ΔPQR, ∠PQR = 90° , seg QS ⊥ side PR such that P-S-R
To prove : ΔPSQ ~ ΔPQR, ΔQSR~ ΔPQR , ΔPSQ ~ QSR
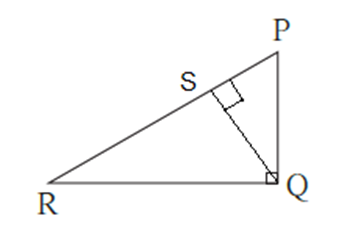
Proof: In ΔPSQ and ΔPQR,
∠QPS ≅ ∠RPQ ……(Common angle)
∠PSQ ≅ ∠PQR …….(Each measures 90°)
∴ ΔPSQ ~ ΔPQR …..(AA test of similarity) …..(1)
In ΔQSR and ΔPQR,
∠SRQ ≅ ∠QRP …….(Common angle)
∠ QSR ≅ ∠PQR …….(Each measures 90°)
∴ ΔQSR ~ ΔPQR ……(AA test of similarity) ….(2)
From (1) and (2), we get
ΔPSQ ~ ΔQSR.
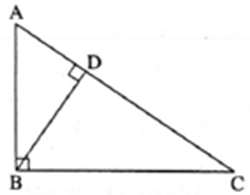
Theorem of geometric mean:
Statement : In a right angled triangle, the perpendicular segment to the hypotenuse from the opposite vertex, is the geometric mean of the segments into which the hypotenuse is divided.
Given ; In ΔABC, ΔABC = 90°. seg BD ⊥ hypotenuse AC such that A-D-C.
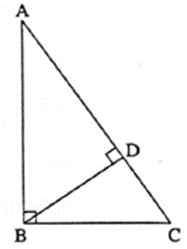
To prove : BD2 = AD × DC
Proof : In ΔABC, ΔABC = 90° ………(Given)
seg BD ⊥ hypotenuse AC
ΔADB ~ ΔBDC ……..(Similarity of right angled triangles)
∴ \(\frac{AD}{BD}=\frac{BD}{DC}\) ………(Corresponding sides of similar triangles are in proportion)
∴ BD2 = AD × DC.
Pythagoras theorem :
Statement : In a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of remaining two sides.
Given : In ΔPQR, ∠PQR = 90°,
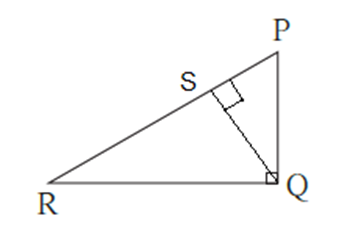
To prove : PR2 = PQ2 + QR2.
Construction ; Draw seg QS ⊥ side PR such that P-S-R.
Proof : In ΔPQR,
∠PQR = 90° ……(Given)
Seg QS ⊥ hypotenuse PR ….(Construction)
∴ ΔPSQ ~ ΔQSR~ ΔPQR …. (Similarity of right angled triangles) …..(1)
ΔPSQ ~ ΔPQR ……[From (1)]
∴ \(\frac{PS}{PQ}=\frac{PQ}{PR}\) ….(Corresponding sides of similar triangles are in proportion)
PQ2 =PS × PR ….(2)
ΔQSR~ΔPQR …..[From (1)]
∴ \(\frac{SR}{QR}=\frac{QR}{PR}\) ……(Corresponding sides of similar triangles are in proportion)
QR2 = SR × PR …..(3)
Adding (2) and (3), we get,
PQ2 + QR2 = PS × PR + SR × PR
PQ2 + QR2 = PR(PS + SR)
PQ2 + QR2 = PR × PR (P—S—R)
PQ2 + QR2 = PR2 OR PR2 = PQ2 + QR2.
Converse of Pythagoras theorem :
In a triangle if the square of one side is equal to the sum of the squares of the remaining two sides, then the triangle is a right angled triangle.
Given : In ΔABC, AC2 = AB2 + BC2
To prove : ΔABC = is a right angled triangle
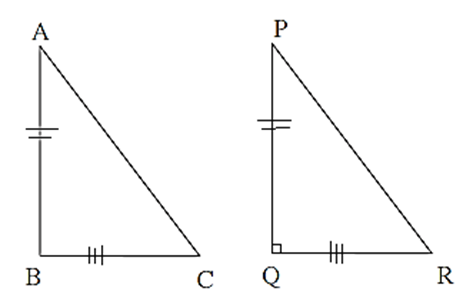
Construction : Draw ΔPQR such that ΔPQR = 90°,
PQ = AB and QR = BC.
Proof : In ΔPQR,
ΔPQR = 90° ….(Construction)
∴ by Pythagoras theorem,
PR2 = PQ2 + QR2 ….(1)
But PQ = AB ...(2), QR = BC …..(3) …….(Construction)
∴ PR2 = AB2 + BC2 ……[From (1), (2) and (3)] ……(4)
Now, AC2 = AB2 + BC2 …..(Given) ……(5)
∴ from (4) and (5), we get,
PR2 = AC2
PR = AC ……(Taking square roots on both the sides) …(6)
In ΔABC and ΔPQR,
seg AB ≅ seg PQ …..(Construction)
seg BC ≅ seg QR …..(Construction)
seg AC ≅ seg PR ….[From (6)]
∴ ΔABC ≅ ΔPQR ….(SSS test of congruence)
∴ ∠ABC ≅ ∠PQR …..(c.a.c.t.)
∠PQR = 90° …(Construction)
∴ ∠ABC = 90°
∴ ΔABC is right angled triangle.
| Remember :
1) Similarity of Right angled triangles :
In ΔABC, if ∠ABC = 90° and seg BD ⊥ hypotenuse AC, then ΔABC ~ ΔADB ~ ΔBDC 2) Theorem of geometric mean :
In ΔPQR, if ∠PQR = 90° and seg QS ⊥ hypotenuse PR, then QS2 = PS × SR. 3) Pythagoras theorem :
In ΔPQR, if ∠PQR = 90°, then PR2 = PQ2 + QR2. 4) Converse of Pythagoras theorem :
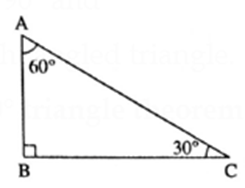
In ΔPQR. if PR2 = PQ2 + QR2, then ΔPQR = 90° and ΔPQR is a right angled triangle. 5) 30°- 60°- 90° triangle theorem :
In ΔABC, if ∠C =30°, ∠A= 60° and ∠B = 90°, then AB = \(\frac{1}{2}\)AC and BC = \(\frac{\sqrt{3}}{2}\)AC 6) Converse of 30°- 60°- 90° triangle theorem :
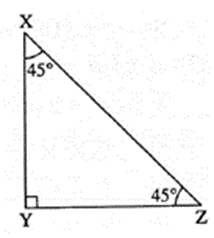
In ΔPQR, if ∠PQR = 90° and PQ = \(\frac{1}{2}\)PR, then ∠PRQ = 30°. 7) 45°- 45°- 90° triangle theorem :
In ΔXYZ, ∠XYZ = 90°, ∠YXZ = ∠XZY = 45° then XY = YZ = \(\frac{1}{\sqrt{2}}\) × XZ |
Application of Pythagoras theorem
Let’s understand the application of Pythagoras theorem to acute and obtuse angled triangles.
Consider the following examples :
(i) In acute angled triangle ABC, seg AD ⊥ side BC, B-D-C, ∠B < 90°; then
AC2 = AB2 + BC2 - BC2 - 2BC.BD
Proof : In ΔADB, ∠ADB = 90°.
∴ by Pythagoras theorem,
AB2 = AD2 + BD2 ……(1)
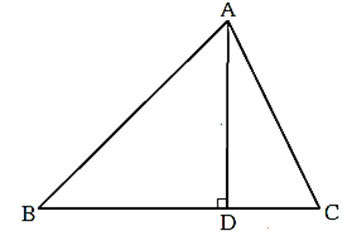
In ΔADC, ∠ADC = 90°.
∴ by Pythagoras theorem,
AC2 = AD2 + DC2
∴ AC2 = AD2 + (BC — BD)2 ……(B—D—C)
∴ AC2 = AD2 + BC2 — 2BC.BD + BD2
∴ AC2 = (AD2 + BD2) + BC2 — 2BC.BD
∴ AC2 = AB2 + BC2 — 2BC.BD. ….[From (1)]
(i) In ΔABC, ∠ACB is obtuse angle, seg AD ⊥ seg BC and D—C—B.
Prove that : AB2 = BC2 + AC2 + 2BC.CD
Proof : In ΔADB, ∠ADB = 90°,
∴ by Pythagoras theorem,
AB2 = (BC + CD)2 + AD2
AB2 = BC2 + 2BC.CD + CD2 + AD2 .......... (I)
Similarly, in ΔADC ∠ADC = 90°,
AC2 = CD2 + AD2
∴ AD2 = AC2 - CD2 .......... (II)
∴ substituting the value of AD2 from (II) in (I)
∴ AB2 = BC2+ 2BC.CD + CD2 + AC2 — CD2
∴ AB2 = BC2+ AC2 + 2BC.CD
Apollonius theorem :
In ΔABC, if seg AP is the median then, AB2 + AC2 = 2AP2 + 2BP2.
This result is known as ‘Apollonius theorem’.
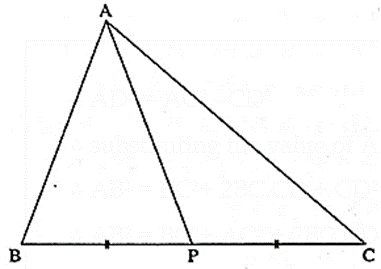
- Apollonius theorem establishes the relation between the sides and median of the triangle.
Statement : In ΔABC, if M is the midpoint of side BC, then AB2 + AC2 = 2AM2 + 2BM2.
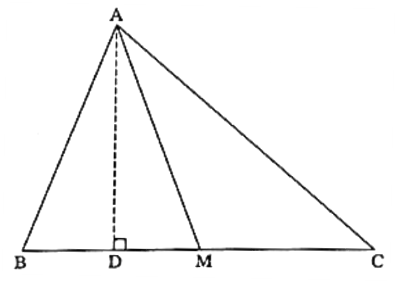
Given : In ΔABC, M is the midpoint of seg BC.
To prove : AB2 + AC2 = 2AM2 + 2BM2.
Construction : Draw seg AD ⊥ side BC such that B-D-C.
Proof : Let’s consider the case, where AM is not perpendicular to seg BC, then out of ∠AMB and ∠AMC, one is acute angle and other is obtuse angle.
Let’s consider ∠AMB as an acute angle and ∠AMC as an obtuse angle.
∠ABM is an acute angled triangle,
∴ by application of Pythagoras theorem, we get,
AB2 = AM2 + BM2 — 2BM·DM …….(1)
ΔAMC is an obtuse angled triangle.
By application of Pythagoras theorem, we get,
AC2 = AM2 + MC2 + 2MC·DM …….(2)
But MC = BM ………. (M is the midpoint of side BC) ….(3)
Substituting (3) in (2), we get,
AC2 = AM2 + BM2 + 2BM.DM ……..(4)
Adding (1) and (4), we get,
AB2 + AC2 = AM2 + BM2 — 2BM.DM + AM2 + BM2 + 2BM.DM
∴ AB2 + AC2 = 2AM2 + 2BM2
Let’s consider the case, where seg AM ⊥ seg BC.
In ΔAMB, ∠AMB = 90°.
∴ by Pythagoras theorem,
AB2 = AM2 + BM2 ……..(5)
In Δ A AMC, ∠AMC = 90°.
∴ by Pythagoras theorem,
AC2 = AM2 + MC2 ……(6)
But MC = BM …....(M is the midpoint of side BC) ……(7)
∴ AC2 = AM2 + BM2 …… [From (6) and (7)] ……(8)
Adding (5) and (8), We get,
AB2 + AC2 = AM2 + BM2 + AM2 + BM2
∴ AB2 + AC2 = 2AM2 + 2BM2.
Example :
Prove that, the sum of the squares of the diagonals of a rhombus is equal to the sum of the squares of the sides.
Given : c PQRS is a rhombus. Diagonals PR and SQ intersect each other at point T
To prove : PS2 + SR2 + QR2 + PQ2 = PR2 + QS2
Proof : Diagonals of a rhombus bisect each other .
∴ by Apollonius’ theorem,
PQ2 + PS2 = 2PT2 + 2QT2 .......... (I)
QR2 + SR2 = 2RT2 + 2QT2 .......... (II)
∴ adding (I) and (II) ,
PQ2 + PS2+ QR2 + SR2 = 2(PT2 + RT2) + 4QT2
= 2(PT2 + PT2) + 4QT2 .......... (RT = PT)
= 4PT2 + 4QT2
= (2PT) 2 + (2QT) 2
= PR2 + QS2
(The above proof can be written using Pythagoras theorem also.)
We reply to valid query.