Quadrilaterals
Class-9-Mathematics-2-Chapter-5-Maharashtra Board
Notes
|
Topics to be learn :
|
Parallelogram :
A quadrilateral having both pairs of opposite sides parallel is called a parallelogram.

In the figure,
seg AB || seg DC and seg AD || seg BC
Quadrilateral ABCD is a parallelogram.
Theorem : Opposite sides and opposite angles of a parallelogram are congruent.
Given : ABCD is a parallelogram.
It means side AB || side DC,
side AD || side BC.
To prove : seg AD ≅ seg BC ; seg DC ≅ seg AB
∠ ADC ≅ ∠ CBA, and ∠ DAB ≅ ∠ BCD.
Construction : Draw diagonal AC.
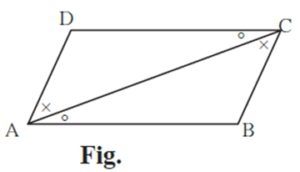
Proof : seg DC || seg AB and diagonal AC is a transversal.
∴ ∠ DCA ≅ ∠ BAC ................(1)
and ∠ DAC ≅ ∠ BCA ..............(2)
Now , in ∆ ADC and ∆ CBA,
∠ DAC ≅ ∠ BCA .......... from (2)
∠ DCA ≅ ∠ BAC .......... from (1)
seg AC ≅ seg CA .......... common side
∴ ∆ ADC ≅ ∆ CBA .......... ASA test
∴ side AD ≅ side CB .......... c.s.c.t.
and side DC ≅ side AB .......... c.s.c.t.,
Also, ∠ ADC ≅ ∠ CBA .......... c.a.c.t.
Similarly we can prove ∠ DAB ≅ ∠ BCD.
| In the above theorem, to prove ∠ DAB = ∠ BCD, draw diagonal BD. The proof is similar to the one given above. |
Theorem : Diagonals of a parallelogram bisect each other.
Given :
PQRS is a parallelogram.
Diagonals PR and QS intersect in point O.
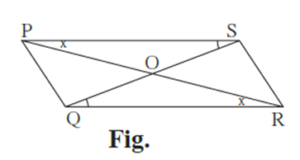
To prove :
seg PO ≅ seg RO,
seg SO ≅ seg QO.
Proof : In ∆POS and ∆ROQ
∠ OPS ≅ ∠ ORQ .......... alternate angles
side PS ≅ side RQ ......... opposite sides of parallelogram
∠ PSO ≅ ∠ RQO .......... alternate angles
∴∆ POS ≅ ∆ ROQ ....... ASA test
∴ seg PO ≅ seg RO and seg SO ≅ seg QO ....... corresponding sides of congruent Triangles
| Remember
· Adjacent angles of a parallelogram are supplementary · Opposite sides of a parallelogram are congruent. · Opposite angles of a parallelogram are congruent. · Diagonals of a parallelogram bisect each other. |
Tests for parallel lines
- If a transversal intersects two lines and a pair of corresponding angles is congruent then those lines are parallel.
- If a transversal intersects two lines and a pair of alternate angles is corgruent then those two lines are parallel.
- If a transversal intersects two lines and a pair of interior angles is supplementary then those two lines are parallel.
Tests of parallelogram :
Theorem : If pairs of opposite sides of a quadrilateral are congruent then that quadrilateral is a parallelogram.
Given : In PQRS
side PS ≅ side QR
side PQ ≅ side SR
To prove : PQRS is a parallelogram.
Construction : Draw diagonal PR

Proof : In ∆ SPR and ∆ QRP
side PS ≅ side QR ........given
side SR ≅ side QP ........ given
side PR ≅ side RP ........ common side
∴ D SPR ≅ D QRP ...... sss test
∴ ∠ SPR ≅ ∠ QRP ....... c.a.c.t.
Similarly, ∠ PRS ≅ ∠ RPQ ..... c.a.c.t.
∠ SPR and ∠ QRP are alternate angles formed by the transversal PR of seg PS and seg QR.
∴ side PS || side QR ......(I) alternate angles test for parallel lines.
Similarly, ∠ PRS and ∠ RPQ are the alternate angles formed by transversal PR of seg PQ and seg SR.
∴ side PQ || side SR ......(II) .....alternate angle test
∴ from (I) and (II) PQRS is a parallelogram.
Theorem : If both the pairs of opposite angles of a quadrilateral are congruent then it is a parallelogram.
Given : In EFGH ∠ E ≅ ∠ G and ∠ H ≅ ∠ F

To prove : EFGH is a parallelogram.
Proof : Let ∠ E = ∠ G = x and ∠ H = ∠ F = y
Sum of all angles of a quadrilateral is 3600
∴ ∠ E + ∠ G + ∠ H + ∠ F = 3600
∴ x + y + x + y = 3600
∴ 2x + 2y = .....
∴ x + y = 180°
∴ ∠ G + ∠ H = 180°
∠ G and ∠ H are interior angles formed by transversal HG of seg HE and seg GF.
∴ side HE || side GF .......... (I) interior angle test for parallel lines.
Similarly, ∠ G + ∠ F = 180°
∴ side HG || side EF .......... (II) interior angle test for parallel lines.
∴ From (I) and (II), EFGH is a parallelogram.
Theorem : If the diagonals of a quadrilateral bisect each other then it is a parallelogram.
Given : Diagonals of ABCD bisect each other in the point E.
It means seg AE ≅ seg CE and seg BE ≅ seg DE

To prove : ABCD is a parallelogram.
Proof : In ∆ AEB and ∆ CED,
seg AE ≅ seg CE ... (Given)
∠ AEB ≅ ∠ CED ... (Vertically opposite angles)
seg BE ≅ seg DE ... (Given)
∴ ∆ AEB ≅ ∆ CED ... (SAS test of congruence)
∴ ∠ BAE ≅ ∠ DCE ... (c.a.c.t.)
i.e. ∠ BAC ≅ ∠ DCA ... (A -E -C)
∴ seg AB || seg DC …..(Alternate angles test for parallel lines) ... (1)
Similarly, we can prove seg AD || seg BC ... (2)
In ABCD
seg AB || seg DC ... [From (1)]
seg AD || seg BC ... [From (2)]
ABCD is a parallelogram ... (By definition)
Theorem : A quadrilateral is a parallelogram if a pair of its opposite sides is parallel and congruent.
Given : In ABCD
seg CB ≅ seg DA and seg CB || seg DA

To prove : ABCD is a parallelogram.
Construction : Draw diagonal BD.
Proof :
seg CB || seg DA ... (Given)
and line BD is the transversal.
∴ ∠ CBD ≅ ∠ ADB ... (Alternate angles) ... (1)
In ∆ CBD and ∆ ADB,
seg CB seg AD ... (Given)
∠ CBD ≅ ∠ ADB ... [From (1)]
seg BD ≅ seg DB ... (Common side)
∴ ∆ CBD ≅ ∆ ADB ... (SAS test of congruence)
∴ ∠ CDB ≅ ∠ ABD ... (c.a.c.t)
∴ seg CD || seg AB ... (Alternate angles test for parallel lines) ... (2)
In ABCD
seg CB || seg DA ... ... (Given)
seg CD || seg AB ... [From (2)]
ABCD is a parallelogram ... (By definition)
| Remember :
· A quadrilateral is a parallelogram, if its pairs of opposite angles are congruent. · A quadrilateral is a parallelogram, if its pairs of opposite sides are congruent. · A quadrilateral is a parallelogram, if its diagonals bisect each other. · A quadrilateral is a parallelogram, if a pair of its opposite sides is parallel and congruent. · These theorems are called tests for parallelogram. |
Example : Q-1. Points D and E are the midpoints of side AB and side AC of D ABC respectively. Point F is on ray ED such that ED = DF. Prove that AFBE is a parallelogram.
Given : (i) In ∆ ABC, D and E are midpoints of sides AB and AC respectively.
(ii) Point F is on ray ED.
(iii) AD ≅ DB, DF ≅ DE

To prove : AFBE is a parallelogram.
Proof : seg AB and seg EF are diagonals of AFBE
seg AD ≅ seg DB …….(D is the midpoint of seg AB)
seg DE ≅ seg DF ... (Construction)
∴ diagonals of AFBE bisect each other.
∴ AFBE is a parallelogram by diagonal test.
Properties of rectangle, rhombus and square :
Rhombus : A quadrilateral is a rhombus, if all of its sides are congruent.
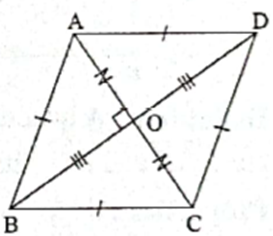
Properties :
- All sides of a rhombus are congruent.
- Opposite angles of a rhombus are congruent.
- Diagonals of a rhombus are perpendicular bisectors of each other.
Rectangles : A quadrilateral is a rectangle, if all of its angles are right angles.
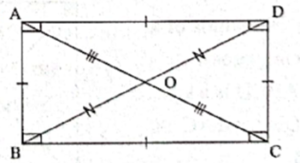
Properties :
- Opposite sides of a rectangle are congruent.
- All angles of a rectangle are congruent.
- Diagonals of a rectangle are congruent and they bisect each other.
Theorem : Diagonals of a rectangle are congruent.
Given : ABCD is a rectangle
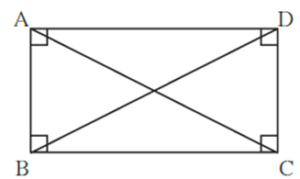
To prove : Diagonal AC ≅ diagonal BD
Proof : In ∆ ABC and ∆ DCB,
seg AB ≅ seg DC ... (Opposite sides of a rectangle)
∠ ABC ≅ ∠ DCB ... (Each measures 90°)
seg BC ≅ seg CB ... (Common side)
∴ ∆ ABC ≅ ∆ DCB ... (SAS test of congruence)
∴ seg AC ≅ seg DB ... (c.s.c.t)
i.e. diagonal AC ≅ diagonal BD.
Square : A quadrilateral is a square, if all of its sides are equal and all of its angles are right angles.
Properties :
- All sides of a square are congruent.
- All angles of a square are congruent.
- Diagonals of a square are congruent and are perpendicular bisectors of each other.
Theorem : Diagonals of a square are congruent.
Given : ABCD is a square.

To prove : Diagonal AC ≅ diagonal DB.
Proof : In ∆ ABC and ∆ DCB,
seg AB ≅ seg DC ... (Sides of a square)
∠ ABC ≅ ∠ DCB ... (Each measures 90°)
seg BC ≅ seg CB ... (Common side)
∴ ∆ ABC ≅ ∆ DCB ... (SAS test of congruence)
∴ seg AC ≅ seg DB ... (c.s.c.t)
i.e. diagonal AC ≅ diagonal DB.
Theorem : Diagonals of a rhombus are perpendicular bisectors of each other.
Given : EFGH is a rhombus
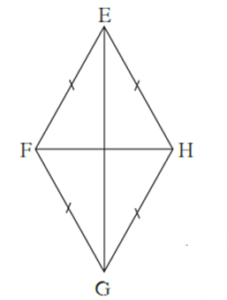
To prove : (i) Diagonal EG is the perpendicular bisector of diagonal HF.
(ii) Diagonal HF is the perpendicular bisector of diagonal EG.
Proof : (i) seg EF ≅ seg EH and seg GF ≅ seg GH ... (Sides of a rhombus are equal)
Every point which is equidistant from end points of a segment is on the perpendicular bisector of the segment.
∴ point E and point G are on the perpendicular bisector of seg HF.
One and only one line passes through two distinct points.
∴ line EG is the perpendicular bisector of diagonal HF.
∴ diagonal EG is the perpendicular bisector of diagonal HF.
(ii) Similarly, we can prove that diagonal HF is the perpendicular bisector of EG.
Theorem : Diagonals of a square are perpendicular bisectors of each other.
Given : EFGH is a square
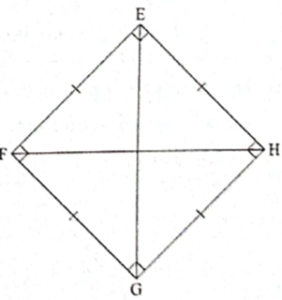
To prove :
(i) Diagonal EG is the perpendicular bisector of diagonal HF.
(ii) Diagonal HF is the perpendicular bisector of diagonal EG.
Proof :
(i) EF = EH, GF = GH ... (Sides of a square are equal)
∴ points E and G are equidistant from the endpoints F and H of seg FH.
∴ point E and G lie on the perpendicular bisector of seg FH ... (Perpendicular bisector theorem)
One and only one line passes through two distinct points and every segment has one and only one perpendicular bisector.
∴ diagonal EG is the perpendicular bisector of diagonal HF.
(ii) Similarly, we can prove that diagonal HF is the perpendicular bisector of diagonal EG.
Theorem : Diagonals of a rhombus bisect its opposite angles.
Given : ABCD is a rhombus.
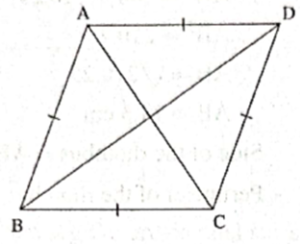
To prove :
Diagonal AC bisects ∠ BAD and ∠ BCD.
Diagonal BD bisects ∠ ABC and ∠ ADC:
Proof : In ∆ ABC and ∆ ADC,
side AB ≅ side AD, side BC ≅ side DC, ... (Sides of a rhombus)
side AC ≅ side AC ... (Common side)
∴ ∆ ABC ≅ ∆ ADC ... (SSS test of congruence)
∴ ∠ BAC ≅ ∠ DAC and ∠ BCA ≅ ∠ DCA ... (c.a.c.t.)
∴ diagonal AC bisects ∠ BAD and ∠BCD.
Similarly, diagonal BD bisects ∠ ABC and ∠ ADC.
Theorem : Diagonals of square bisect its opposite angles.
Given : ABCD is a square.

To prove :
Diagonal AC bisects ∠ BAD and ∠ BCD.
Diagonal BD bisects ∠ ABC and ∠ ADC.
Proof : In ∆ ABC and ∆ ADC,
side AB ≅ side AD, side BC ≅ side DC
... (Sides of a square are equal)
side AC ≅ side AC ... (Common side)
∴ ∆ ABC ≅ ∆ ADC ... (SSS test of congruence)
∴ ∠ BAC ≅ ∠ DAC, ∠ BCA ≅ ∠DCA ... (c.a.c.t.)
Similarly, diagonal BD bisects ∠ ABC and ∠ ADC.
∴ diagonal AC bisects ∠ BAD and ∠ BCD.
Similarly, diagonal BD bisects ∠ ABC and ∠ ADC.
Trapezium :
When only one pair of opposite sides of a quadrilateral is parallel, then the quadrilateral is called a trapezium.
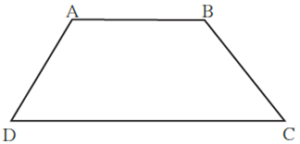
In the figure seg AB and seg DC are parallel sides,
seg AD and seg BC are non-parallel sides.
ABCD is a trapezium.
In the figure, by property of parallel lines,
∠ A + ∠ D = 180° and ∠ B + ∠ C = 180°.
Isosceles trapezium : If non-parallel sides of a trapezium are congruent, then that quadrilateral is called an isosceles trapezium.

In the figure, seg PQ || seg SR and seg PS ≅ seg QR.
PQRS is an isosceles trapezium.
Median of the trapezium : The segment joining the midpoints of non-parallel sides of a trapezium is called the median of the trapezium.

In the figure, P and Q are the midpoints of non-parallel sides AB and DC of trapezium ABCD respectively. Therefore, seg PQ is the median of the trapezium.
Example : Q.1 Measures of angles of ABCD are in the ratio 4 : 5 : 7 : 8. Show that ABCD is a trapezium.
Solution : Let measures of ∠ A, ∠ B, ∠ C and ∠ D are (4x)°, (5x)°, (7x)°, and (8x)° respectively.
Sum of all angles of a quadrilateral is 360°.
∴ 4x + 5x + 7x + 8x = 360
∴ 24x = 360, ∴ x = 15
∠ A = 4 × 15 = 60°, ∠ B = 5 × 15 = 75°, ∠ C = 7 × 15 = 105°, and ∠ D = 8 × 15 = 120°
Now , ∠ B + ∠ C = 75° + 105°= 180°
∴ side CD || side BA...... (I)
But ∠ B + ∠ A = 75°+ 60°= 135° ¹ 180°
∴ side BC and side AD are not parallel .........(II)
∴ ABCD is a trapezium. ..........[from (I) and (II)]
Theorem of midpoints of two sides of a triangle :
Theorem : The segment joining midpoints of any two sides of a triangle is parallel to the third side and half of it.
Given : In ∆ ABC, point P is the midpoint of seg AB and point Q is the midpoint of seg AC
To prove : seg PQ || seg BC and PQ = BC
Construction :
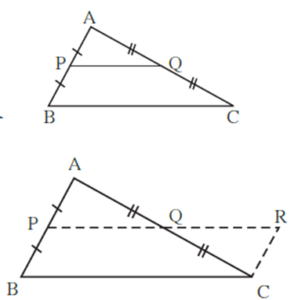
Produce seg PQ upto R such that PQ = QR
Draw seg RC.
Proof : In ∆ AQP and ∆ CQR
seg PQ ≅ seg QR ...... construction
seg AQ ≅ seg QC ...... given
∠ AQP ≅ ∠ CQR ..... vertically opposite angles.
∴ ∆ AQP ≅ ∆ CQR ....... SAS test
∠ PAQ ≅ ∠ RCQ ..... (1) c.a.c.t.
∴ seg AP ≅ seg CR ......(2) c.s.c.t.
From (1) line AB || line CR .........alternate angle test
from (2) seg AP ≅ seg CR
Now, seg AP ≅ seg PB ≅ seg CR and seg PB || seg CR
∴ PBCR is a parallelogram.
∴ seg PQ || seg BC and PR = BC ..... opposite sides are congruent
PQ = PR ...... (construction)
∴ PQ = BC ∵ PR = BC ... (Opposite sides of a parallelogram)
∴ seg PQ || seg BC and PQ = BC.
Converse of midpoint theorem :
Theorem : If a line drawn through the midpoint of one side of a triangle and parallel to the other side, then it bisects the third side.
Given : Point D is the midpoint of seg AB.
Line l passing through the point D and parallel to side BC intersects side AC in point E.

To prove : AE = EC.
Construction : Through point C, draw line CF || side AB to intersect line l at F such that D-E-F.
Proof : line CF || line AB ... (Construction)
and line AC is the transversal,
∴ ∠ DAC ≅ ∠ FCA ... (Alternate angles)
i.e. ∠ DAE ≅ ∠ FCE ... (A-E-C) ... (1)
In DBCF,
side DF || side BC
side DB || side CF
DBCF is a parallelogram
∴ seg DB ≅ seg CF ... (Opposite sides of a parallelogram) ... (2)
also, seg DB seg AD ... (D is the midpoint of seg AB) ... (3)
∴ from (2) and (3), we get,
seg AD ≅ seg CF ... (3)
In ∆ ADE and ∆ CFE,
∠ DAE ≅ ∠ FCE
∠ AED ≅ ∠ FEC
∴ ∠ ADE ≅ ∠ CFE ... (Remaining angles of the triangles) ... (5)
seg AD ≅ seg CF ... [From (4)]
From (1), (4) and (5),
∆ ADE ≅ ∆ CFE ... (ASA test of congruence)
∴ seg AE ≅ seg CE ... (c.s.c.t.)
∴ AE = CE
i.e. line l bisects side BC.
Example : Q-1. Points E and F are mid points of seg AB and seg AC of ∆ ABC respectively. If EF = 5.6 then find the length of BC.

Solution : In ∆ ABC, point E and F are midpoints of side AB and side AC respectively.
EF = ½ BC .......midpoint theorem
5.6 = ½ BC ∴ BC = 5.6 × 2 = 11.2
PDF-Notes,Solution,Text Book
PDF : Class 9th-Mathematics-2-Chapter-5-Quadrilaterals-Notes
PDF : Class 9th-Mathematics-2-Chapter-5-Quadrilaterals-Solution
Main Page : – Maharashtra Board Class 9th-Mathematics – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter-4-Constructions of Triangles – Online Notes
Next Chapter : Chapter-6-Circle – Online Notes
We reply to valid query.